Why Beauty is Truth (60 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart


The history of mathematics shows repeatedly that it is dangerous to dismiss some clever or beautiful idea merely because it has no obvious utility. Unfortunately, this does not stop people from dismissing such ideas, often
because
they are beautiful or clever. The more “practical” people consider themselves to be, the more they tend to heap scorn on mathematical concepts that arise from abstract questions, invented “for their own sake” instead of addressing some real-world issue. The prettier the concept is, the greater the scorn, as if prettiness itself were a reason to be ashamed.
Such declarations of uselessness are hostages to fortune. It takes only one new application, one new scientific advance, and the despised concept may suddenly plonk itself down on center stageâno longer useless, but essential.
The examples are endless. Cayley himself said his matrices were completely useless, but today no branch of science could function without them. Cardano declared complex numbers to be “as subtle as they are useless,” but no engineer or physicist could function in a world that lacked complex numbers. Godfrey Harold Hardy, England's leading mathematician in the 1930s, was immensely pleased that number theory had no practical application, and in particular that it could not be used in warfare. Today number theory is used to encrypt messages into code, a technique that is vital to secure Internet commerce, and even more vital to the military.
So it is turning out with the octonions. They may yet become a compulsory topic in mathematics courses, and even more so in physics. It is now emerging that the octonions are of central importance in the theory of Lie groupsâespecially those of interest in physics, especially the five exceptional Lie groups G
2
, F
4
, E
6
, E
7
, and E
8
, with their weird dimensions 14, 52, 78, 133, and 248. Their very existence is a puzzle. One exasperated mathematician declared them a brutal act of Providence.

Lovers of nature enjoy revisiting well-known beauty spots and finding a new vantage point . . . halfway down a waterfall, just along a ledge leading
off to the side of the well-worn footpath, on a promontory overlooking a blue ocean vista. In the same way, mathematicians like to revisit old topics and look at them from new points of view. As our perspective on mathematics changes, we can often reinterpret old concepts in new, insightful ways. This is not just a matter of mathematical tourism, gazing open-mouthed at the ineffable from a different angle. It provides new, powerful ways to tackle old and new problems. Nowhere has this tendency been more apparent, or more informative, than in the theory of Lie groups.
Recall that Killing organized almost all simple Lie groups into four infinite families, two of which are really parts of one larger family, the special orthogonal groups SO(
n
) in even and odd dimensions. The other two are the special unitary groups SU(
n
) and the symplectic groups Sp(2
n
).
We now know that these families are all variations on the same theme. They consist of all
n
Ã
n
matrices satisfying a particular algebraic conditionâthey are “skew-Hermitian.” The only difference is that you have to use matrices of real numbers to get the orthogonal Lie algebras, matrices of complex numbers to get the unitary Lie algebras, and matrices of quaternions to get the symplectic Lie algebras. These algebras come in infinite families because matrices come in infinitely many sizes. It is wonderful to see that the Lie algebras corresponding to the natural transformations of Hamilton's version of mechanics, his first great discovery, have a natural description in terms of quaternions, his last.
It does make you wonder what happens when you use octonions as entries in the matrix. Unfortunately, because of the lack of associativity, you don't get a new infinite family of simple Lie algebras. Actually, that should be “fortunately,” since we know that no such family exists. But when you play the right games with octonions, and have the law of small numbers on your side, you can get Lie algebras with a vengeance.
The first hint that this might be the case came in 1914, when Ãlie Cartan answered an obvious question and got a surprising answer. A guiding principle in mathematics and physics is that if you have some interesting object, the first thing to ask is what its symmetry group looks like. The symmetry group of the real number system is trivial, consisting of only the identity transformation “do nothing.” The symmetry group of the complex number system contains the identity and one mirror symmetry, which transforms
i
into â
i
. The symmetry group of the quaternions is SU(2), which is very nearly the rotation group SO(3) in real three-dimensional space.
Cartan asked, What is the symmetry group of the octonions?
If you are a Cartan, you can also answer this question. The symmetry group of the octonions is the smallest exceptional simple Lie group, the one known as G
2
. The 8-dimensional system of octonions has a 14-dimensional symmetry group. The exceptional normed division algebra is directly related to the first of the exceptional Lie groups.

To proceed further, we need to take on board one more idea, which goes back to the Renaissanceâbut to the artists, not the mathematicians.
In those days, mathematics and art were rather close; not just in architecture but in painting. The Renaissance painters discovered how to apply geometry to perspective. They found geometric rules for drawing images on paper that really looked like three-dimensional objects and scenes. In so doing, they invented a new and extremely beautiful kind of geometry.
The work of earlier artists does not look quite realistic to our eyes. Even a painter like Giotto (Ambrogio Bondone) managed to produce works with an almost photographic quality, but on close analysis the perspective is not completely systematic. It was Filippo Brunelleschi who, in 1425, formulated a systematic mathematical method for obtaining accurate perspective, which he then taught to other artists. By 1435 we find the first book on the topic, Leone Alberti's
Della Pittura.
The method was brought to perfection in the paintings of Piero della Francesca, who was also a consummate mathematician. Piero wrote three books on the mathematics of perspective. And it would be impossible not to mention Leonardo da Vinci, whose
Trattato della Pittura
begins by stating, “Let no one who is not a mathematician read my works,” an echo of the slogan “Let no one ignorant of geometry enter” which legendarily was placed over the door of Plato's academy in ancient Greece.
The essence of perspective is the notion of “projection,” by which a three-dimensional scene is rendered on a flat sheet of paper by (conceptually) drawing each point of the scene to the viewer's eye, and seeing where that line meets the paper. A key idea is that projections distort shapes in ways not permitted by Euclid. In particular, projection can turn parallel lines into lines that meet.
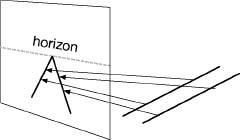
How projection makes parallels meet at the horizon.
We see this effect every day. When we stand on a bridge and see a long, straight railroad track or highway disappearing into the distance, the lines converge and seem to meet at the horizon. The real lines remain the same distance apart, but perspective causes the perceived distance to shrink as the lines get farther away from us. In a mathematical idealization, infinitely long parallel lines in a plane also meet if they are suitably projected. But the place where they meet is not the image of anything in the planeâit can't be; they don't meet in the plane. It is the apparent “horizon” toward which the lines, and the plane, extend. On the plane itself, the horizon is infinitely distant, but its projection is a perfectly sensible line across the middle of the picture.
This line is known as the “line at infinity.” Like the square root of minus one, it is a fiction, but an extremely useful one. The kind of geometry that emerges is called projective geometry, and in the spirit of Klein's Erlangen program, it is the geometry of those features of a scene that are not changed by projections. Every artist who makes perspective drawings with a horizon line and “vanishing points” to organize his or her images to look like real objects is using projective geometry.
In a projective plane, geometry is very elegant. Any two points can be joined by a unique line, just as in Euclid's geometry. But any two distinct lines meet, too, at exactly one point. Parallels, which so exercised Euclid, do not exist.
If this reminds you of the Fano plane, you're right. The Fano plane is a finite projective geometry.

From Renaissance perspective to the exceptional Lie groups is now but a short step. The projective plane that was implicit in Alberti's methods was made explicit as a new kind of geometry. In 1636, Girard Desargues, an army officer who later became an architect and engineer, published
Proposed Draft of an Attempt to Treat the Results of a Cone Intersecting a Plane.
It sounds like a book on conics, and it was, but instead of using the traditional Greek geometry, Desargues used projective methods. Just as Euclidean geometry could be turned into algebra by using Descartes's coordinates (
x, y
), a pair of real numbers, so projective geometry could be turned into algebra by letting
x
or
y
become infinite (in a cleverly controlled manner, involving ratios of three coordinates and setting 1 ÷ 0 = infinity).
