World's 200 Hardest Brain Teasers (14 page)

If the original three against three don’t balance, take the three balls that tip the scale downward and weigh two of those balls, one on one side, the other on the other. If they balance, it’s the remaining ball. If they don’t balance, it’s the ball that tips the scale downward.

147. The man is 52 and his wife is 39.

Denote the man’s age now as
M
, the wife’s age now as
W
, the man’s age when he was as old as the wife now as
m,
the wife’s age when the man was as old as she is now as
w
.

Then we get

(1)
M
+
W
= 91

(2)
m
=
W
(since the man was then as old as the wife now)

(3)
M
= 2
w
(since the man is twice as old as the wife was)

The key thing to realize is that the difference in ages between the man and his wife now is the same difference then or at any other time. That is,

(4)
M
-
W
=
m
-
w

So substituting (2) and (3) into (4), we get

M
-
W
=
W
-
M
/2 or
M
-
W
= (2
W
-
M
)/2, which gives us 2
M
- 2
W
= 2
W
-
M
, so we get

(5) 3
M
= 4
W
or
M
= 4
W
/3

We substitute (5) into (1) and we get:

4
W
/3 +
W
= 91; 7
W
/3 = 91 and
W
= 273/7 = 39. From (1) we get
M
+ 39 = 91, and so
M
= 52.

148. 45/50 or 90 percent

n
= nickels,
p
= pennies,
q
= quarters,
d
= dimes

We have 5
n
+
p
+ 10
d
+ 25
q
= 100 (since the total is 100 cents) and
n
+
p
+
d
+
q
= 50 (since the total is 50 coins).

Subtract the two equations:

We get 4
n
+ 9
d
+ 24
q
= 50.

Suppose
q
= 1. Then 4
n
+ 9
d
+ 24 = 50, and so 4
n
+ 9
d
= 26.

The only way this is possible is if
d
= 2 and
n
= 2.

Suppose
q
= 2. Then 4
n
+ 9
d
+ 48 = 50, and we get 4
n
+ 9
d
= 2, which is impossible.

So we have 1 quarter, 2 dimes, and 2 nickels, which leaves 45 pennies since the total number of coins is 50. If I drop 1 penny, we have the probability as 45/50 or 90 percent.

149. (e) 108

Translate: The number of apples that Bill bought =
B,
that Harry bought =
H,
and that Martin bought =
M
. “Bill bought four times as many apples as Harry” translates to
B
= 4
H.
Similarly
B
= 3
M. “
Bill, Harry, and Martin purchased a total of less than 190 apples” translates to
B
+
H
+
M
< 190. You will find that manipulating these equations, we get
B
< 120. However, because
H
and
M
are integers,
B
= 108 and not 119!

Here’s the complete solution:

(1)
B
+
H
+
M
< 190

(2)
B
= 4
H

(3)
B
= 3
M

Substituting (3) into (1) we get

(4) 3
M
+
H
+
M
< 190

From (2) and (3), we get

(5) 3
M
= 4
H
and so

(6)
H
= 3
M
/4

Substituting (6) into (4) we get

(7) 3
M
+ 3
M
/4 +
M
< 190

This becomes

(8) 19
M
/4 < 190 and thus

(9)
M
/4 < 10, so
M
< 40. So at this point you might think that
M
= 39. And from (3),
B
becomes 117. But from (6) we wouldn’t have H as a whole number! The greatest number less than 40 which the whole number
M
could be for (6) to be true is
M
= 36. Then
H
= 27, and from (3),
B
= 108.

150.

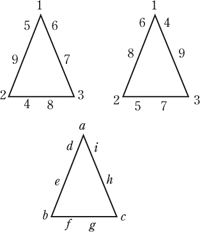
Let’s see what numbers would be on the vertices of the triangle. Represent those numbers by
a, b,
and c. Let the numbers 1 through 9 be represented by a, b, c,
d, e, f, g, h, i.
Then we have

(1)
a
+
e
+ d +
b
= 17

(2)
b
+
f
+
g
+
c
= 17

(3)
c
+
h
+
i
+
a
= 17

(4)
a
+
b
+
c
+
d
+
e
+
f
+
g
+
h
+
i
= 45 (since all the numbers 1 + 2 + 3…9 add up to 45)

Adding (1), (2), (3) we get

(5) 2
a
+ 2
b
+ 2
c
+
d
+
e
+
f
+
g
+
h
+
i
= 51.

Subtracting (4) from (5) we get
a
+
b
+
c
= 6. The only way this can be possible is if the numbers for
a
,
b
, and
c
are 1, 2, 3.

So start with the numbers 1, 2, and 3 at the vertex of the triangle. For the left side, since the numbers must add up to 17, the other two numbers on the left side must add up to 14. The only possibilities are 6 and 8 or 5 and 9. If it is 5 and 9, then the remaining numbers are 4, 6, 7, 8. For the bottom side, two of these numbers (of 4, 6, 7, 8) must add up to 17 - 5 = 12. The only way is 4 and 8. So then we’d have 6 and 7 left. For the right side, 1 + 3 + 6 + 7 adds up to 16. Similarly you can see that for the left side 6 and 8 also works and we get the triangle on the right.

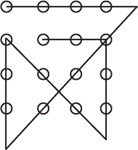
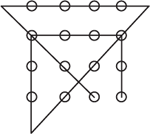
151. There are at least four different solutions.

Think outside of the box. Draw lines outside of the square that contains the circles.

Solution 1

Solution 2

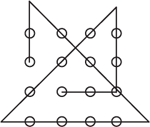
Note that the two ends can be extended to form a continuous path. There are four points external to the 4 x 4 array.

Solution 3

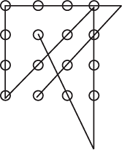
Solution 4

152. (c) There is the same amount of water in the alcohol as alcohol in the water.

Let’s say the cup of alcohol you pour in the water contains
c
gallons (c could be 1/10, for example). Now the water bucket has a mixture of alcohol and water. Now you pour one cup (again,
c
gallons) of that mixture back into the alcohol bucket. Let’s say there are
a
gallons of alcohol and
w
gallons of water in that cup. So (1)
a
+
w
=
c
.

Now the amount of water poured into the alcohol is
w.
The amount of alcohol in the water bucket is
c
-
a,
since we poured
a
gallons of alcohol into the alcohol bucket from the water bucket. From (1) we get
c
-
a
=
w,
so (c) is true.

153. (e) octagon

Here’s the figure:

154. (d) e

The sequence is arranged in pairs: st no jk gh

Note that we have a pattern: gh (i) jk (lm) no (pqr) st

The letters in parentheses increase by one letter in the sequence. Thus, the next two letters in the original sequence must be e, f, since the pattern will be preserved:

ef (no letters) gh (i) jk (lm) no (pqr) st

155. 
x
/2 +
y

You
may have gotten the answer x
/2 -
y,
but that’s how many people are left on the bus!

x
- (x/2 - y), which is x/2 + y, is the answer.

156. LIGHTS, CAMERA, ACTION

157. (b) 2

Write an equation, where
n
is the number of nickels,
d
is the number of dimes, and
q
is the number of quarters: 5
n
+ 10
d
+ 25
q
= 100. Start with the smallest numbers for
n
,
d
, and
q
that satisfy the equation. Start with
n
= 0,
d
= 0, then
q
= 4, which is not true since the most
q
can be is 3. Then try
n
= 0,
d
= 1. Then we get 25
q
= 90, which doesn’t give us a whole number for
q.
You will find that if
n
= 1,
d
= 2, and
q
= 3, and if
n
= 3,
d
= 1, and
q
= 3, you will satisfy the equation. So there are two ways to make change.