World's 200 Hardest Brain Teasers (16 page)
Read World's 200 Hardest Brain Teasers Online
Authors: Dr. Gary R. Gruber

The sum of the lengths of two sides of a triangle must be greater than the third side. So, 4 + 5 >
x
and
x
+ 6 >
y.
Thus, since 9 >
x
, we can set up a single inequality and add 6 to both sides to get 15 >
x
+ 6. But
x
+ 6 >
y,
so 15 >
x
+ 6 >
y,
and so 15 >
y
. The perimeter of the figure is 4 + 5 + 6 +
y
= 15 + y. Since 15 >
y
, 15 +
y
(the perimeter) is less than 30.
198. The fractions are equal. They are both equal to 2/1.
199. (b) “I will be shot.”
If he says, “I will be shot,” that statement is neither true nor false. If it were true, he would be hanged. But then “being shot” wouldn’t have been true. Thus, the statement must be false. But if it were false, he would be shot. But if he were shot, the statement would have been true. So there is a contradiction, and his statement was neither true nor false. They couldn’t shoot him or hang him. So they let him free. Actually what happened was that they shot him anyway.
200. (c) 11
Houses that have fewer than six rooms is 10 (given). Houses that have six, seven, or eight rooms is
x
(unknown). Houses that have more than eight rooms is 4 (given). The total is 25. 10 +
x
+ 4 must equal 25, so
x
must be 11.
201. 1.
train
or
drain
2.
craft
or
draft
3.
stone
4.
write
5.
blame
or
flame
6.
stall
7.
phone
8.
troll
9.
place
10.
grace
11.
crush
12.
crave
13.
swine
14.
swarm
15.
scold
16.
scorn
17.
scone
18.
sworn
19.
spark
20.
plate
There are also many more, including sword, spear, stream, spool, etc.
202. They are all exactly divisible by the product of their digits. For example, take 112. 1 x 1 x 2 = 2 and 112/2 = 56.
203. In order for the horse to move, the horse pushes back on the ground. This makes the ground push back on the horse (this is actually Newton’s third law). Thus, there is a force exerted by the ground on the horse, which enables the horse to move with the cart.
204.
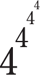
That is, 4 to the fourth power to the fourth power to the fourth power—quite a huge number.
205. (e) 400
So you don’t have to rack your brain in a verbal math problem, always translate “what” to
x
, “percent” to /100, “of ” to
x
(times), and “is” to =. In the problem above, you would get:
What percent of 5 is 20?
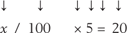
This becomes: (
x
/100) x 5 = 20.
Now here’s another strategy. Get rid of the fractions! Multiply both sides of the equation above by 100. You get:
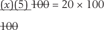
and you find
(x)(5) = 20 x 100 = 2,000; Divide both sides of the equation by 5:
x
= 400.
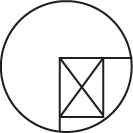
206. 5”
Draw extra lines to get more information. Draw the radius. The radius of the circle is the same as the diagonal of the rectangle!
207. First weighing: four against four
Second weighing: two against two
Third weighing: one against one
Try to find a set of balls as “reference” balls, none of which is the heavy or light ball.
Note that even though the scale may tip downward in one direction, the heavy ball may not be on the “downward” part of the scale; it may be that the lighter ball is on the upward side.
Let’s work through the solution:
Identify balls by number 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
(1, 2, 3) ? (4, 5, 6) means you weigh 1, 2, 3 vs. 4, 5, 6
If the result of weighing is (1, 2, 3) < (4, 5, 6), it means first group (1, 2, 3) is lighter than the second, (4, 5, 6).
(1, 2, 3) > (4, 5, 6) means the first group (1, 2, 3) is heavier. (1, 2, 3) = (4, 5, 6) means both groups (1, 2, 3) and (4, 5, 6) weigh the same and so all the balls in that group are normal.
N
represents a normal ball.
Divide 12 balls into 3 groups: (1, 2, 3, 4), (5, 6, 7, 8), (9, 10, 11, 12).
First weighing: weigh (1, 2, 3, 4) ? (5, 6, 7, 8)
CASE 1: Where (1, 2, 3, 4) = (5, 6, 7, 8)
This means that the odd ball is in (9, 10, 11, 12) and that 1, 2, 3, 4, 5, 6, 7, 8 are normal
(N)
Second weighing: weigh (N, 9) ? (10, 11)
If (N, 9) = (10, 11)
This means the odd ball is 12.
Third weighing: weigh (12) ? (
N
).
If (12) > (
N
) then 12 is the heavy ball. If (12) < (
N
), then 12 is the light ball.
If in the second weighing, (N, 9) > (10, 11), then either 9 is heavy or 10 or 11 is light.
Third weighing: weigh (10) ? (11).
If (10) > (11), then 11 is light and 9 is normal. If (10) < (11), then 10 is light.
If in weighing (10) ? (11), (10) = (11), then 9 must be heavy.
If in the second weighing, (N, 9) < (10, 11), you can similarly reason that 9 is light or 10 or 11 is heavy.
And then in the third weighing, weigh (10) ? (11).
If (10) > (11), then 10 is heavy. If (10) < (11), then 11 is heavy. If (10) = (11), then 9 is light.
CASE 2: Where in the first weighing, (1, 2, 3, 4) > (5, 6, 7, 8) .
Then you know that 9, 10, 11, 12 are normal (
N),
and one of the balls 1, 2, 3, 4 is heavy or one of the balls 5, 6, 7, 8 is light.
Second weighing: weigh (
N,
1, 2) ? (3, 4, 5)
If (N, 1, 2) = (3, 4, 5) then the odd ball is in (6, 7, 8) and is lighter, so weigh (6) ? (7) and pick the lightest. If (6) = (7) then 8 is light.
If
(N,
1, 2) > (3, 4, 5), (3, 4) are normal, so odd is in (1, 2, 5).
Third weighing: weigh (1) ? (2).
If (1) > (2) then 1 is heavy; if (1) < (2), then 2 is heavy; if (1) = (2), then 5 is light.
Second weighing: For the case where (N, 1, 2) < (3, 4, 5), the odd ball is in (3, 4) and is heavy, since 5 can’t be heavy, and (1, 2), which were in the heavy group originally, are not the heavy ones, now.
Third weighing: So weigh (3) ? (4). If (3) > (4), 3 is heavy. If (3) < (4), then 4 is heavy.
CASE 3: Where in the first weighing, (1, 2, 3, 4) < (5, 6, 7, 8).
Second weighing: weigh (N, 1, 2) ? (3, 4, 5). If (N, 1, 2) = (3, 4, 5), odd ball is in (6, 7, 8) and is heavier, so weigh (6) ? (7) (third weighing) and pick the heaviest. If (6) = (7), then 8 is heavy.
If (
N,
1, 2) > (3, 4, 5), the odd ball is in (3, 4) and is light, since according to the first weighing, (5) can’t be light and (1, 2) cannot be heavy.
Third weighing: So weigh (3) ? (4). If (3) > (4), then 4 is light. If (3) < (4), then 3 is light.
If in the second weighing, (
N,
1, 2) < (3, 4, 5), then either (1,2) is light or 5 is heavy because of the first weighing.
Third weighing: So weigh (1) ? (2). If (1) > (2), then 2 is light. If (1) < (2), then 1 is light. If (1) = (2), then 5 is heavy.
208. (b) The third student’s hat can be white.
Think of what information you get by knowing that both the first and second students cannot figure out the color of their hats.
The color of the third student’s hat is red. He reasons, “If I can prove it’s impossible that I have a white hat, then I must have a red hat.” There are only three scenarios in which the last student could have a white hat:
(1) if the first student has a red hat and the second student has a white hat,
(2) if the first student has a white hat and the second student has a red hat, and
(3) if both the first and second students have red hats.
Scenario (1) is ruled out because the first student would have known his hat was red if the other two students had white hats, since there were only two white hats in the original bag. Scenario (2) is ruled out because the second student would have made the same deduction. Scenario (3) is ruled out because the second student would have known she was wearing a red hat if the third student was wearing a white hat, because otherwise the first student would have seen that they were both wearing white hats. But because the second student did not know or figure out that she was wearing a red hat, the third student could not be wearing a white hat. Thus the only combinations are (where A, B, C denote first, second, third student respectively):
A—White; B—White; C—Red
A— White; B—Red; C—Red
A—Red; B—White; C—Red
A—Red; B—Red; C—Red
Thus, (b) is correct.
209. 3 to 4
Translate from words to math. Let
S
be the ship’s age now;
B
is the boiler’s age now; s is the ship’s age then; and
b
is the boiler’s age then. You would get:
(1)
S
= 2
b
(2)
s
=
B
(3)
B/S
unknown
(4)
B
-
b
=
S
- s, because
B
-
b
and
S
-
s
represents the same passage of time.
Substituting (1) in the left side of (4) and (2) in the right side of (4), we get:
(5)
B
-
S
/2 =
S
-
B
Thus, we get:
(6) 2
B
= 3
S
/2 or
(7)
B/S
= 3/4
210. 9/20
Call females F1, F2, F3, and call males M1, M2, M3. The total number of combinations of three people, such as F1, F2, M1 and F1, M2, M3, etc., is six combinations taken three at a time, or 6C3, which is equal to (6 x 5 x 4) / (3 x 2 x 1) = 20. The favorable number of combinations is nine:
M1, M2, F1
M1, M2, F2
M1, M2, F3
M1, M3, F1
M1, M3, F2
M1, M3, F3
M2, M3, F1
M2, M3, F2
M2, M3, F3
Thus the probability of only two males in the room is favorable ways / total ways = 9/20.
THE GEOMETRY PROBLEM THAT STUMPED THE NATION
