X and the City: Modeling Aspects of Urban Life (41 page)

Obviously this last case is intermediate between the other two in the sense that as the inner beltway radius
r
₁
→ 0,
T
₃
→
T
₁
, and as the outer radius
r
₁
→
r
₀
,
T
₃
→
T
₂
. It is interesting to compare these travel times; so let us examine the first two cases and ask when it is quicker to travel along the outer beltway to
P
, that is, when is
T
₂
<
T
₁
? This inequality can be arranged as

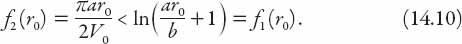
Since
f
₁
(0) =
f
₂
(0) = 0, and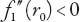
, it follows that the graphs of these two functions will intersect at some radius,
r
_c
say, if and only if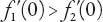
, i.e., if 2
V
₀
> (
π
−
θ
)
b
. If
r
_c
<
r
₀
then there will be an interval (0,
r
_c
) for which it is quicker (in this model) to travel along the outer beltway to
P
. If
r
_c
>
r
₀
then the curves do not intersect and it is always quicker to use the outer beltway.

We can think about the growth of cities in several ways, none of them prurient, despite the title of this chapter. Perhaps the most obvious one is how the population changes over time; another is how the civic area changes; yet another might be the number of businesses or companies in the city; and so on. These statistical properties are generally referred to as
demographics
, and they can include gender, race, age, population density, homeownership, and employment status, to name but a few. In this chapter we shall focus attention on some the simplest possible models of population growth in several different contexts, ending with some using “real” data from a bygone era. We’ll start with exponential growth.

In the November 4, 1960, issue of the journal
Science
, a paper [
28
] was published with the following provocative title: “Doomsday: Friday 13 November, A.D. 2026.” Beneath this was the sentence:
At this date human population will approach infinity if it grows as it has grown in the last two millennia
.

The authors presented a formula for the population
P
in terms of positive constants
A
,
b
, and
t
_D
(to be defined below) as

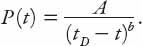
In this equation, the subscript
D
stands for “Doomsday”! We proceed to derive more simply a form of this result to illustrate the principle behind it. But first, a caveat. In what follows, differential calculus is used. So what’s the problem with that? Well, in so doing, we are making the implicit assumption of differentiability, and hence continuity of the population of interest, whether it be humans, bedbugs, or tumor cells. But the populations are discrete! In these models, there are
always
an integral number of people, bedbugs, and so on. Calculus is strictly valid only when there is a continuum of values of the variables concerned and the dependent variables are differentiable functions. In that sense continuum models can never be totally realistic, even when there are billions of individuals (such as the number of cells in a tumor). Nevertheless, if there are sufficiently many individuals, we can justifiably approximate the properties of the population and its growth using calculus. Further informal discussion of one aspect of this “discrete/continuum” problem can be found in
Appendix 8
. Now we can begin!

Everyone has heard of “exponential growth” but not everyone knows what it means. It applies to (here, differentiable) functions
P
(
t
) for which the growth rate is proportional to
P
, or equivalently, the “per capita” growth rate is a constant,
k
. In mathematical terms

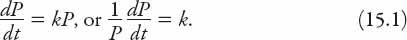
If we know that at some time
t
= 0 say, the population is
P
₀
, then the solution of equation (15.1) is

If
k
< 0, then
P
decreases exponentially from its initial value of
P
₀
. Such exponentially decreasing solutions are used in many algebra books to illustrate the phenomenon of radioactive decay. If
k
> 0 we see an immediate problem: the solution grows without bound as
t
→ ∞. This is reasonably supposed to be unrealistic, because if
P
represents the population of a city, country, or the world, there is not an unlimited supply of resources to maintain that growth. In fact, the English clergyman Thomas Malthus (1766–1834) wrote an essay in 1798 stating that “The power of population is indefinitely greater than the power in the earth to produce subsistence for man.” This has been paraphrased to say that populations grow geometrically while resources grow arithmetically. Not surprisingly, exponential growth is sometimes referred to as “Malthusian growth.”

Let’s modify equation (15.1) just a little, and examine the innocuous looking first-order ordinary differential equation

(with
P
(0) =
P
₀
as before). For reasons discussed below we will restrict the parameter
ε
to the range −1 <
ε
< ∞. This simple looking
nonlinear
ordinary differential equation has some surprises in store for us, and in fact is sometimes referred to as the “Doomsday” equation. The first thing to do is integrate it to obtain