XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (95 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay
XPath 2.0 offers a full range of arithmetic operators and functions on
xs:decimal
values. These are summarized in the entry for
xs:double
which follows this entry. The arithmetic operators are described in more detail in Chapter 8, and the functions are listed in Chapter 13. When you apply these operators and functions to
xs:decimal
operands, the result is generally also an
xs:decimal
. In the case of operators with two operands, you can mix
xs:decima
l with other numeric types; if the other operand is an
xs:float
or
xs:double
, then the
xs:decimal
is converted to an
xs:float
or
xs:double
as appropriate, and the result will also be an
xs:float
or
xs:double
.
The main operation that can cause problems is division. The division operator in XPath is
div
, because
/
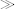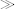is reserved for use in path expressions. Division by zero is a fatal error. When you perform a division that does not have an exact decimal result, for example10 div 3.0, the precision of the result is implementation-defined. One implementation might give you 3.333333, another might give you 3.333333333333. An implementation could even claim to be conformant if it gave you the answer 3, though it might not prove popular in the marketplace if it did that.
When a decimal number is displayed as a string, it is shown as an integer if there are no significant digits after the decimal point. So the result of2.5 + 2.5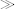is displayed as5.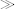
xs:double
The
xs:double
type represents double-precision floating-point numbers. This was the only numeric type supported in XPath 1.0, and it is therefore the default for some operations where backward compatibility is important; in particular, if you apply numeric operations to the value of a node in a schemaless document, the system will try to convert the contents of that node to an
xs:double
value.
An
xs:double
is a double-precision (64-bit) floating-point number, and its behavior is defined to follow the IEEE 754 standard. This standard (
IEEE Standard for Binary Floating-Point Arithmetic
.
ANSI/IEEE Std. 754-1985
) has been widely implemented by many microprocessors for some years, but it is only through its adoption in the Java language that it has become familiar to high-level language programmers. If you understand how floating point behaves in Java, the contents of this section will be quite familiar; if not, they may be rather strange.
XPath 2.0 introduces the ability to use scientific notation for floating-point numbers, either on input or on output. If you want to enter the number one trillion, you can now write
1.0E12
. In fact, if you want to write an
xs:double
as a literal in an XPath expression, you must write it in scientific notation: otherwise, it will be treated as an
xs:decimal
(if it has a decimal point) or as an
xs:integer
(if not).
On output, that is when you convert an
xs:double
to a string, scientific notation is used only if the absolute value is smaller than 0.000001, or greater than 1,000,000. This means that most everyday numbers will be formatted in ordinary decimal notation on output. In XSLT, you can control the format of numeric output more precisely by using the
format-number()
function, which is described in Chapter 13.
In general, I recommend using
xs:double
for numbers that are on a continuous scale (for example, distances, weights, or temperatures), and using
xs:decimal
for numbers that represent discrete quantities, such as sums of money. But this is only rough guidance.
IEEE 754 defines the following range of values for a double-precision number:
| Value | Description |
| Finite nonzero values | These are values of the form s × m × 2 e , where s (the sign) is +1 or –1, m (the mantissa) is a positive integer less than 2 53 , and e (the exponent) is an integer between –1075 and 970, inclusive |
| Positive zero | This is the result of subtracting a number from itself. It can also result from dividing any positive number by infinity, or from dividing a very small number by a very large number of the same sign. |
| Negative zero | This is the result of dividing any negative number by infinity. It can also result from dividing a positive number by minus infinity, or from dividing a very small negative number by a very large positive number, or vice versa. |
| Positive infinity | This is the result of dividing any positive number by zero. It can also result from multiplying two very large numbers with the same sign. Note that division by zero is not an error: it has a well-defined result. |
| Negative infinity | This is the result of dividing any negative number by zero. It can also result from multiplying two very large numbers with different signs. |
| NaN | Not a Number. This is the result of attempting to convert a non-numeric string value to a number. It can also be used to mean “unknown” or “not applicable”, like the SQL null value. |
These values cannot all be written directly as XPath constants. However, they can be expressed as the result of expressions, for example:
| Value | XPath expression |
| Negative zero | –0e0 |
| Positive Infinity | 1 div 0e0 |
| Negative Infinity | –1 div 0e0 |
| NaN | number(“NaN”) |
Technically, negative numbers cannot be written directly as constants:-10is an expression rather than a number, but in practice it can be used anywhere that a numeric constant can be used. The only thing you need to be careful of is that a space may be needed before the unary minus operator if you write an expression such as$x div -1.
