Zero (23 page)
Authors: Charles Seife

Unfortunately for Cantor, not everyone had the same vision of God. Leopold Kronecker was an eminent professor at the University of Berlin, and one of Cantor's teachers. Kronecker believed that God would never allow such ugliness as the irrationals, much less an ever-increasing set of Russian-doll infinities. The integers represented the purity of God, while the irrationals and other bizarre sets of numbers were abominationsâfigments of the imperfect human mind. Cantor's transfinite numbers were the worst of the lot.
Disgusted with Cantor, Kronecker launched vitriolic attacks against Cantor's work and made it extremely difficult for him to publish papers. When Cantor applied for a position at the University of Berlin in 1883, he was rejected; he had to settle for a professorship at the much less prestigious University of Halle instead. Kronecker, who was influential at Berlin, was likely to blame. The same year, he wrote a defense against Kronecker's attacks. Then, in 1884, the depressed Cantor had his first mental breakdown.
It would be little comfort to Cantor that his work was the foundation of a whole new branch of mathematics: set theory. Using set theory, mathematicians would not only create the numbers we know out of nothing at all, they would create numbers that were previously unheard ofâinfinite infinities that can be added to, multiplied with, subtracted from, and divided by other infinities, just like ordinary numbers. Cantor opened up a whole new universe of numbers. The German mathematician David Hilbert would say, “No one shall expel us from the paradise which Cantor has created for us.” But it was too late for Cantor. Cantor was in and out of mental institutions for the remainder of his life, and he died in the mental hospital at Halle in 1918.
In the battle between Kronecker and Cantor, Cantor would ultimately prevail. Cantor's theory would show that Kronecker's precious integersâand even the rational numbersâwere nothing at all. They were an infinite zero.
There are an infinite number of rationals, and between any two numbers you choose, no matter how close together, there are still an infinite number of rationals. They are everywhere. But Cantor's hierarchy of infinities would tell a different tale: it would show just how little space the rational numbers take up on the number line.
It takes a clever trick to do such an intricate calculation. Irregularly shaped objects can be very difficult to measure. For instance, imagine that you've got a stain on your wood floor. How much area does the stain take up? It's not so obvious. If the stain were shaped like a circle, or like a square or a triangle, it would be easy to figure out; just take a ruler and measure its radius or its height and base. But there's no formula for figuring out the area of an amoeba-shaped mess. However, there is another way.
Take a rectangular carpet and place it on top of the stain. If the carpet covers the stain entirely, we know that the stain is smaller than the carpet; if the carpet is one square foot, then the stain must take up less than one square foot. If we use smaller carpets, our approximation gets better and better. Perhaps the stain is covered by five carpets of size one-eighth square foot; we would then know that the stain takes up at most five-eighths of a square foot, which is less than our approximation with a one-square-foot carpet. As you make the carpets smaller and smaller, the covering gets better and better, and your total carpet area approaches the true size of the stain; in fact, you can define the size of the stain as the limit as your carpets approach zero size (Figure 43).
Let's do the same thing with the rational numbersâbut this time our carpets are sets of numbers. For instance, the number 2.5 is “covered” by a carpet that includes, for example, all the numbers between 2 and 3âa carpet of size 1. Using this sort of carpet to cover the rational numbers has some very odd consequences, as Cantor soon showed, thanks to his seating chart. That seating chart accounts for all the rational numbersâit assigns each of them a seatâso we can count them off one by one, in order, based on their seat number. Take the first rational number and imagine it on the number line. Let's cover it with a carpet of size 1. Lots of other numbers are covered by that carpet, but we don't have to worry about that. So long as the first number is covered, we are happy.
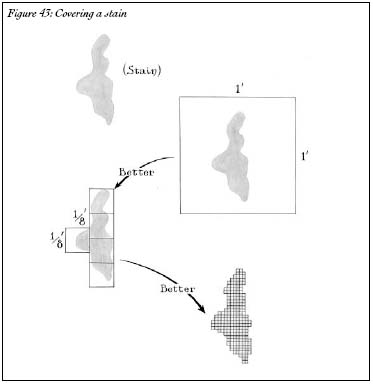
Figure 43: Covering a stain
Now take the second number. Cover it with a carpet of size ½. Take the third number and cover it with a carpet of size ¼, and so forth. Go on and on to infinity; since every rational number is on the seating chart, every rational number will eventually be covered by a carpet. What is the total size of the carpets? It's our old friend, the Achilles sum. Adding up the size of the carpets, we see 1 + ½ + ¼ +
1
/
8
+â¦+ ½
n
goes to 2 as
n
goes to infinity. So we can cover the infinite cohorts of rational numbers in the number line with a set of carpets, and the total size of the carpets is 2. This means that the rational numbers take up less than two units of space.
Just as we did with the stain, let's make the carpet sizes even smaller to get a better approximation of the size of the rationals. Instead of starting with a carpet of size 1, starting with a carpet of size ½ makes the total size of the carpets equal to 1; the rational numbers take up less than one unit of space, in total. If we start off with an initial carpet that has size 1/1000, all the carpets, in total, take up less than 1/500 unit of space; all the rational numbers take up less room than 1/500 unit. If we start with a carpet the size of half an atom, we can cover all the rational numbers on the number line with carpets that, in total, take up less room than an atom. Yet even those tiny carpets, all of which can fit in the span of an atom, cover all of the rational numbers (Figure 44).
We can get smaller and smallerâas small as we want. We can cover the rationals with carpets that, summed together, fit in the size of half an atomâor a neutronâor a quarkâor as small as we can possibly imagine.
How big are the rational numbers, then? We defined size as a limitâthe sum of the carpets as the individual sizes go to zero. Yet at the same time, we saw that as the carpets get smaller and smaller, the sum of the cover gets tinier and tinierâsmaller than an atom or a quark or a millionth-billionth part of a quarkâand we can still cover the rationals. What is the limit of something that gets smaller and smaller and smaller without stopping?
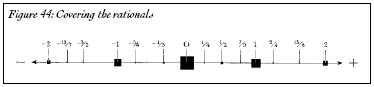
Figure 44: Covering the rationals
Zero.
How big are the rational numbers? They take up no space at all. It's a tough concept to swallow, but it's true.
Even though there are rational numbers everywhere on the number line, they take up no space at all. If we were to throw a dart at the number line, it would
never
hit a rational number. Never. And though the rationals are tiny, the irrationals aren't, since we can't make a seating chart and cover them one by one; there will always be uncovered irrationals left over. Kronecker hated the irrationals, but they take up
all
the space in the number line.
The infinity of the rationals is nothing more than a zero.
7
Absolute Zeros
[THE PHYSICS OF ZERO]
Sensible mathematics involves neglecting a quantity when it is smallânot neglecting it because it is infinitely great and you do not want it!
âP. A. M. D
IRAC
I
t was finally unmistakable: infinity and zero are inseparable and are essential to mathematics. Mathematicians had no choice but to learn to live with them. For physicists, however, zero and infinity seemed utterly irrelevant to the workings of the universe. Adding infinities and dividing by zeros might be a part of mathematics, but it is not the way of nature.
Or so scientists had hoped. As mathematicians were uncovering the connection between zero and infinity, physicists began to encounter zeros in the natural world; zero crossed over from mathematics to physics. In thermodynamics a zero became an uncrossable barrier: the coldest temperature possible. In Einstein's theory of general relativity, a zero became a black hole, a monstrous star that swallows entire suns. In quantum mechanics, a zero is responsible for a bizarre source of energyâinfinite and ubiquitous, present even in the deepest vacuumâand a phantom force exerted by nothing at all.
Zero Heat
When you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind: it may be the beginning of knowledge, but you have scarcely, in your thoughts, advanced to the stage of
science.
âW
ILLIAM
T
HOMSON
, L
ORD
K
ELVIN
The first inescapable zero in physics comes from a law that had been in use for half a century. This law was discovered in 1787 by Jacques-Alexandre Charles, a French physicist already famous for being the first to fly aboard a hydrogen balloon. Charles isn't remembered for his aeronautic stunts, but for the law of nature that bears his name.
Charles, like many physicists of his time, was fascinated with the very different properties of gases. Oxygen makes embers burst into flame, while carbon dioxide snuffs them out. Chlorine is green and is deadly; nitrous oxide is colorless and makes people giggle. Yet all these gases have very basic properties in common: heat them up and they expand; cool them down and they contract.
Charles discovered that this behavior is extremely regular and predictable. Take an equal volume of any two different gases and put them in identical balloons. Heat them up by the same amount and they expand by the same amount; cool them down together and they contract in unison. Furthermore, for each degree up or down you go, you gain or lose a certain percentage of the volume. Charles' law describes the relationship of the volume of a gas to its temperature.
In the 1850s, however, William Thomson, a British physicist, noticed something odd about Charles' law: the specter of zero. Lower the temperature and the volume of the balloons gets smaller and smaller. Keep lowering at a steady pace and the balloons keep shrinking at a constant rate, but they cannot go on shrinking forever. There is a point at which gas, in theory, takes up no space at all; Charles' law says that a balloon of gas must shrink to zero space. Of course, zero space is the smallest possible volume; when a gas reaches this point, it takes up no space at all. (It certainly can't take up negative space.) If the volume of a gas is related to its temperature, a minimum volume means that there is a minimum temperature. A gas cannot keep getting colder and colder indefinitely; when you can't shrink the balloon any further, you can't lower the temperature any further. This is
absolute zero.
It is the lowest temperature possible, a little more than 273 degrees Celsius below the freezing point of water.
Thomson is better known as Lord Kelvin, and it is for Kelvin that the universal temperature scale is named. In the centigrade scale, zero degrees is the freezing point of water. In the Kelvin scale, zero degrees is absolute zero.
Absolute zero is the state where a container of gas has been drained of all of its energy. This is, in actuality, an unattainable goal. You can never cool an object to absolute zero. You can get very close; thanks to laser cooling, physicists can chill atoms to a few millionths of a degree above the ultimate coldness. However, everything in the universe is conspiring to stop you from actually reaching absolute zero. This is because any object that has energy is bouncing aroundâand radiating light. For instance, people are made up of molecules of water and a few organic contaminants. All of these atoms are wiggling about in space; the higher the temperature, the faster the atoms wiggle. These wiggling atoms bump into one another, getting their neighbors to wiggle as well.
Say you are trying to cool a banana to absolute zero. To get rid of all of the energy in the banana, you've got to stop its atoms from moving around; you have to put it in a box and cool it down. However, the box the banana is in is made of atoms, too. The box's atoms are wiggling around, and they will bump the banana's atoms and set them in motion again. Even if you get the banana to float in a perfect vacuum in the center of the box, you can't stop the wiggling entirely, because dancing particles give off light. Light is constantly coming off of the box and striking the banana, getting the banana's molecules to move again.
All of the atoms that make up a tweezer, a refrigerator coil, and a tub of liquid nitrogen are moving and radiating, so the banana is constantly absorbing energy from the wiggles and radiation of the box it is in, from the tweezers you use to manipulate the banana, and from the refrigerator coil you use to cool it down. You cannot shield the banana from the box or the tweezer or the coil; the shield, too, is wiggling and radiating. Every object is influenced by the environment it's in, so it's impossible to cool anything in the universeâa banana, an ice cube, a dollop of liquid heliumâto absolute zero. It is an unbreakable barrier.
Absolute zero was a discovery that had a very different flavor from Newton's laws. Newton's equations gave physicists power. They could predict the orbits of the planets and the motion of objects with great accuracy. On the other hand, Kelvin's discovery of absolute zero told physicists what they
couldn't
do. They couldn't ever reach absolute zero. This barrier was disappointing news to the physics world, but it was the beginning of a new branch of physics: thermodynamics.
Thermodynamics is the study of the way heat and energy behave. Like Kelvin's discovery of absolute zero, the laws of thermodynamics erected impenetrable barriers that no scientists can ever cross, no matter how hard they try. For instance, thermodynamics tells you that it is impossible to create a perpetual-motion machine. Avid inventors tend to swamp physics departments and science magazines with blueprints for incredible machinesâmachines that eternally generate power without any source of energy. However, the laws of thermodynamics state that it is impossible to create such a machine. It is another task that cannot be done, no matter how hard you try. It is impossible even to get a machine to run without wasting energy, frittering some of its power into the universe as heat. (Thermodynamics is worse than a casino; you can't win, no matter how much you work at it. You can't even break even.)
From thermodynamics came the discipline of statistical mechanics. By looking at the collective motion of groups of atoms, physicists could predict the way matter behaves. For instance, the statistical description of a gas explains Charles' law. As you raise the temperature of a gas, the average molecule moves faster and smashes harder into the walls of its container. The gas pushes harder on the walls: the pressure goes up. Statistical mechanicsâthe theory of wigglesâexplained some of the basic properties of matter, and it even seemed to explain the nature of light itself.
The nature of light was a problem that had consumed scientists for centuries. Isaac Newton believed that light was composed of little particles that flowed from every bright object. Over time, though, scientists came to believe that light was not in fact a particle, but a wave. In 1801 a British scientist discovered that light interferes with itself, apparently putting the matter to rest once and for all.
Interference happens with all sorts of waves. When you drop a stone into a pond, you create circular ripples in the waterâwaves. The water bobs up and down, and crests and troughs spread outward in a circular pattern. If you drop two stones at the same time, the ripples interfere with one another. You can see this more clearly if you dip two oscillating pistons into a tub of water. When a crest from one piston runs into a trough from the other, the two cancel out; if you look carefully at the pattern of ripples, you can see lines of still, wave-free water (Figure 45).
The same thing is true of light. If light shines through two small slits, there are areas that are darkâwave-free (Figure 46). (You can see a related effect at home. Hold your fingers together; you should have tiny gaps where some light can get through. Gaze through one of those gaps at a lightbulb and you'll see faint dark lines, especially near the top and bottom of the gap. These lines, too, are due to the wavelike nature of light.) Waves interfere in this way; particles do not. Thus, the phenomenon of interference seemed to settle the question of light's nature once and for all. Physicists concluded that light was not a particle, but a wave of electric and magnetic fields.
This was the state of the art in the mid-1800s, and it seemed to mesh perfectly with the laws of statistical mechanics. Statistical mechanics tells you how the molecules of matter wiggle; the wave theory of light implied that these molecular wiggles somehow cause ripples of radiationâlight waves. Better yet, the hotter the object is, the faster its molecules move; at the same time, the hotter the object, the more energetic the ripples of light it sends out. This works out perfectly. With light, the faster the wave bobs up and downâthe higher its frequencyâthe more energy it has. (Also, the higher its frequency, the smaller its
wavelength:
the distance between two wave crests.) Indeed, one of the most important thermodynamic lawsâthe so-called Stefan-Boltzmann equationâseems to tie the wiggles of molecules to the wiggles of light. It relates the temperature of an object to the total amount of light energy it radiates. This was the biggest victory for statistical mechanics and the wave theory of light. (The equation states that the radiated energy is proportional to the temperature raised to the fourth power. It not only tells how much radiation an object gives off, but also how hot an object gets when irradiated with a given amount of energy. This is the law that physicists usedâalong with a passage in the book of Isaiahâto determine that heaven is more than 500 degrees Kelvin.)
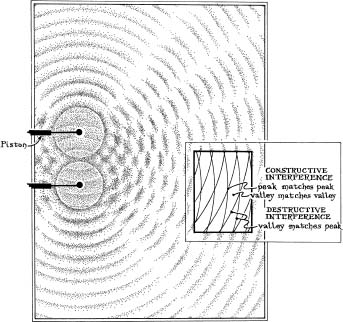
Figure 45: Interference pattern in water
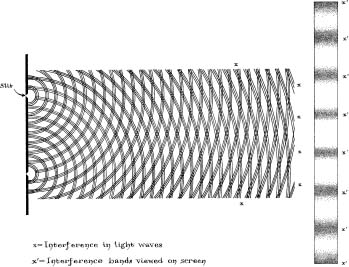
Figure 46: Light interference. If you turn the book sideways and look along the page, you can see the interference patterns on the page.
Unfortunately, the victory would not last for long. At the turn of the century, two British physicists tried to use the wiggle theory to solve a simple problem. It was a fairly straightforward calculation: how much light does an empty cavity radiate? Applying the basic equations of statistical mechanics (which tells how the molecules wiggle) and the equations that describe the way electric and magnetic fields interact (which tells how light wiggles), they came up with an equation that describes what wavelengths of light a cavity radiates at any given temperature.
The so-called Rayleigh-Jeans law, named after the physicists Lord Rayleigh and Sir James Jeans, worked fairly well. It did a good job of predicting the amount of large-wavelength, low-energy light that comes off a hot object. At high energies, though, the equation faltered. The Rayleigh-Jeans law predicted that an object gives off more and more light at smaller and smaller wavelengths (and thus higher and higher energies). Consequently at realms close to zero wavelength, the object gives off an
infinite
amount of high-energy light. According to the Rayleigh-Jeans equation, every object is constantly radiating an infinite amount of energy, no matter what its temperature is; even an ice cube would be radiating enough ultraviolet rays, x rays, and gamma rays to vaporize everything around. This was the “ultraviolet catastrophe.” Zero wavelength equals infinite energy; zero and infinity conspired to break a nice, neat system of laws. Solving this paradox quickly became the leading puzzle in physics.
