Birth of a Theorem: A Mathematical Adventure (9 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

Date: Wed, 19 Nov 2008 10:07:14
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: Re: Sunday IHP
After a good night’s sleep I see now that it’s UNREALISTIC: composing by Omega will NECESSARILY force us to lose a bit on lambda (this is already the case when Omega
=
(1-epsilon) Id). So we’re just going to have to deal with it somehow.
More later.…
Cedric
Date: Wed, 19 Nov 2008 13:18:40
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: update
Updated file attached:
I’ve added subsection 3.2 in which I examine what appears to be a fundamental objection having to do with something we talked about on the phone, the problem of the loss of functional space due to the change of variable. The conclusion is that it isn’t lost, but we’ll have to be very precise in our estimates of the change in variable.
Cedric
Date: Wed, 19 Nov 2008 14:28:46
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: update
New addition at the end of section 3.2. Things now seem rather promising.
Date: Wed, 19 Nov 2008 18:06:37
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: Re: update
I’m pretty sure that section 5 in its present form is wrong!! The problem arises after the phrase “In assigning powers and factorials”: the line that follows seems OK, but in the formula a bit further on the indices don’t match up
(N_{k-i
+
1}/{k-i
+
1}! ought to yield N_k/k!
and not N_k/(k
+
1)!)
The result seems much too strong. It would mean that in composing by an approximation of the identity the same index for the analytic norm is preserved. I think we’ve got to aim instead at something like
\
|
f\circ G\
|
_\lambda \leq const.
\
|
f\
|
_{\lambda \
|
G\
|
} \
|
G\
|
or something along these lines.
More later,
Cedric
Date: Wed, 19 Nov 2008 22:26:10
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: good news
In the attached version I’ve gotten rid of the problematic section 5 (we can always put it back in if we need to) and in its place I’ve put calculations on composition, still using the same analytic variants, which this time seem to work beautifully as far as composition is concerned (the formula I had suggested won’t do, the right one turns out to be even simpler, though still of the same kind).
More later, Cedric
Date: Wed, 19 Nov 2008 23:28:56
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: good news
New version attached. I’ve checked to see that the usual calculation can be done with the norm suggested by the composition rule (section 5.1). It’s only slightly more complicated but it seems to give more or less the same result. That’s all for today.
Cedric
Bourgoin-Jallieu
December 4, 2008
Headlights suddenly loom out of the darkness at the exit from the parking lot. Momentarily blinded, I approach the driver. It’s my third try.
“Excuse me, are you going to Lyon?”
“Uh … yes.”
“Would you be kind enough to give me a lift? The trains have stopped running!”
The driver hesitates for a split second, glances at her passengers, invites me to take a seat in back. I get in.
“Thanks so much!”
“So you were at the concert?”
“Of course! Wasn’t it terrific?”
“Really great, yeah.”
“I wouldn’t have missed the Têtes Raides’ twentieth anniversary tour for anything—but I hate to drive, so I came down by train, thinking I wouldn’t have any problem hitching a ride back.”
“It’s no trouble. I brought along my son and his friend, who’s sitting next to you in back.”
Hello everybody.
“The pogoing wasn’t out of control, there was a lot of room, you weren’t getting stepped on all the time. It was pretty relaxed.”
“The girls had no reason to complain.”
“Oh, some of them love it when it really gets wild!”
Fond memories of one ravishing punk chick in particular, pierced, incredibly full of energy, whom chance threw into my arms one night while dancing at a Pigalle concert in Lyon.
“Nice spider.”
“Thank you. I always wear one, it’s part of who I am. I have them custom-made in Lyon. Atelier Libellule.”
“Are you a musician?”
“No!”
“An artist?”
“A mathematician!”
“A mathematician?”
“Yes—mathematicians
do
exist!”
“What do you work on?”
“Hmmm. Do you
really
want to know?”
“Sure, why not?”
“Yeah, go ahead!”
A deep breath.
“I’ve developed a synthetic notion of Ricci curvature lower-boundedness in complete, locally compact metric-measure spaces.”
“What!?!”
“You must be kidding.”
“Not at all. I wrote an article about it that made a pretty big splash in the community.”
“What’s it about again? Sounds cool.”
“Okay, one more time: a synthetic theory of lower-boundedness of Ricci curvature in metric-measure spaces that are separable, complete, and locally compact.”
“Wow!”
“What’s it good for, anything?”
The ice is broken, we’re off. I start talking, explaining, demystifying. Einstein’s theory of relativity. Curvature—the cornerstone of non-Euclidean geometry—and the deflection of light rays: if the curvature is positive, the rays get closer the farther they travel; if the curvature is negative, the farther they travel the more they diverge. Curvature is usually expressed using the language of optics, but it can also be expressed using the language of statistical physics: density, entropy, disorder, kinetic energy, minimal energy—that’s the discovery I made, with the help of a few other mathematicians. But how can one speak of curvature in a space that’s covered with spikes, like the bristles on the head of a hedgehog? Then there’s the problem of optimal transport, the subject of my thousand-page book. You encounter it everywhere, economics, engineering, meteorology, computer science, geometry.…
I go on and on. The miles fly by.
“We’re coming into town now. Where can I drop you off?”
“I live in the first arrondissement—the intellectuals’ neighborhood! But anywhere that suits you is fine, really. I’ll manage.”
“It’s no problem at all. Just tell me how to get there and we’ll take you home.”
“That would be wonderful. Can I give you some money for the toll?”
“No, absolutely not.”
“That’s very kind of you.”
“Before you go, would you write down a mathematical formula for me?”
* * *
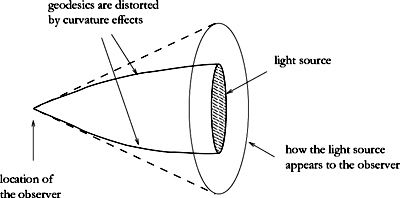
Fig 14.4 – The meaning of distortion coefficients. Because of positive curvature effects, the observer overestimates the surface area of the light source; in a negatively curved world, the observer underestimates it.
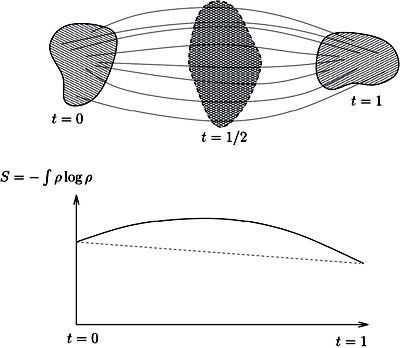
Fig 16.2 – The lazy gas experiment. To go from state 0 to state 1, the lazy gas uses a path of least action. In a nonnegatively curved world, the trajectories of the particles first diverge, then converge, so that at intermediate times the gas can afford to have a lower density (higher entropy).
[From Cédric Villani,
Optimal Transport: Old and New
(Berlin: Springer, 2008), pp. 408, 460, with slight modifications]
A village in the Drôme
December 25, 2008
Back home with family for the holidays. I’ve made a lot of progress.
Four computer files, simultaneously updated as we go along, contain everything we have learned about Landau damping. Four files that we have exchanged, added to, corrected, reworked, and sprinkled with notes—marked “NdCM” in boldface for Clément’s comments, “NdCV” for mine. Composed in the T
E
X language developed by the universal master, Donald Knuth, these files are ideally suited for the preliminary maneuvers we’re engaged in at the moment.
When we got together again in Lyon a while ago for another working session, Clément complained about an inequality that I had inserted in one of the files:

