Birth of a Theorem: A Mathematical Adventure (8 page)

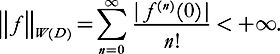
Show that if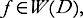
and if g is holomorphic near the values taken by f on
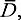then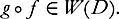
(Remark that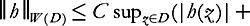
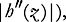and that W
(
D
)
is an algebra; then write

where N is chosen sufficiently large that the series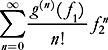
is well defined and converges in W
(
D
)
.)

[Serge Alinhac and Patrick Gérard,
Pseudo-Differential Operators and the Nash–Moser Theorem
(chapter 3, exercise A.1.a)]

*   *   *

Date: Tue, 18 Nov 2008 10:13:41
+
0100

From: Clement Mouhot

To: Cedric Villani

Subject: Re: Sunday IHP

I’ve just seen your last emails, will read them carefully, I’m getting a lot of flak for trying to use my trick in a stability theorem for the solution of the transport equation with small analytic perturbation! More soon! clement

Date: Tue, 18 Nov 2008 16:23:17
+
0100

From: Clement Mouhot

To: Cedric Villani

Subject: Re: Sunday IHP

A quick comment after having looked at a paper by Tao (actually the summary of it that he gives in his blog) on weak turbulence and the cubic 2d defocusing Schrodinger.

His definition of weak turbulence is: shift of mass to increasingly higher frequencies asymptotically, and his definition of strong turbulence is: shift of mass to increasingly higher frequencies within a finite time. Here’s the conjecture he formulates for his equation: Conjecture.* (Weak turbulence) There exist smooth solutions u(t,x) to (1) such that \
|
u(t)\|_{H^s({\Bbb T}^2)} goes to infinity as t \to \infty for any s
>
1.

Remains to be seen whether this can also be shown for the solutions that they’re trying to construct (for free transport, the derivatives in x really blow up). As in our case they need confinement through the torus apparently in order to be able to see this phenomenon without dispersion in the real variable x getting in the way. On the other hand one thing I don’t understand is that he argues the phenomenon is nonlinear and isn’t observed in linear cases. In what we’re looking at it does seem to be found at the linear level …

More later, clement

Date: Wed, 19 Nov 2008 00:21:40
+
0100

From: Cedric Villani

To: Clement Mouhot

Subject: Re: Sunday IHP

Okay, here’s what I’ve done today. I’ve added a few comments to the Estimates file, deleted the first section (which was obsolete, really) and reorganized various estimates that were dispersed in various files, so that now pretty much everything is in a single file.

I don’t think we’re clear yet about the norm we should be working in:

– since the equation on \rho in the case of a homogenous field is integral only in time (!) we have to work in a fixed norm, which therefore must be _stable_ under composition by \Om.

– Fourier seems unavoidable if we’re going to be able to convert the analytic into exponential decay. I don’t know how to do the exponential convergence directly without Fourier, obviously it must be possible.

– since the change of variable is in (x,v) and the Fourier transform of \rho is a Dirac in \eta, it looks like what we need is an analytic norm of the L^2 in k and L^1 in \eta type.

– but the composition will certainly never be continuous in an L^1 space, so that can’t be right, probably we’ll have to be fairly devious and begin by “integrating” the \etas. That would leave an L^2 analytic norm in the variable k.

Conclusion: We’ll have to go on being devious.

More later,

Cedric

Date: Wed, 19 Nov 2008 00:38:53
+
0100

From: Cedric Villani

To: Clement Mouhot

Subject: Re: Sunday IHP

On 19/11/08, 00:21, Cedric Villani wrote:

>
Conclusion: We’ll have to go on being devious.

Right now I have the impression that in order to find a way around this difficulty we’ll need the theorem on continuity of composition by Omega for the L^2 analytic norm in Fourier (without loss of generality…), treating \eta as a parameter. Talk to you tomorrow:-)