Birth of a Theorem: A Mathematical Adventure (4 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

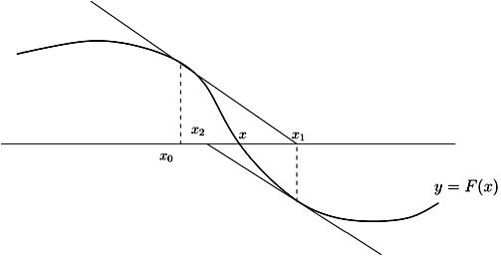
A few years after formulating the law of gravitation, Newton made another extraordinary discovery: an iterative method for calculating the solutions of any equation of the form
F
(
x
)
=
0.
Starting from an approximate solution x
0
,
you replace the function F by its tangent T
x
0
at the point
(
x
0
,
F
(
x
0
))
(more precisely, the equation is linearized around x
0
)
and solve the approximate equation T
x
0
(
x
)
=
0. This gives a new approximate equation x
1
,
and you now repeat the same procedure: replace F by its tangent T
x
1
at x
1
,
obtain x
2
as the solution of T
x
1
(
x
2
)
=
0, and so on. In exact mathematical notation, the relation that associates x
n
with x
n
+
1
is
x
n
+
1
=
x
n
−
[
DF
(
x
n
)]
−
1
F
(
x
n
).
The successive approximations x
1
,
x
2
,
x
3
,
… obtained in this fashion are incredibly good: they approach the “true” solution with phenomenal swiftness. It is often the case that four or five tries are all that is needed to achieve a precision greater than that of any modern pocket calculator. The Babylonians are said to have used this method four thousand years ago to extract square roots; Newton discovered that it can be used to find not only square roots but the roots of any real-valued equation.
Much later, the same preternaturally rapid convergence made it possible to demonstrate some of the most striking theoretical results of the twentieth century, among them Kolmogorov’s stability theorem and Nash’s isometric embedding theorem. Single-handedly, Newton’s diabolical scheme transcends the artificial distinction between pure and applied mathematics.

Isaac Newton
* * *
The Russian mathematician Andrei Kolmogorov is a legendary figure in the history of twentieth-century science. In the 1930s, Kolmogorov founded modern probability theory. His theory of turbulence in fluid dynamics, worked out in 1941, remains the starting point for research on this subject today, both for those who seek to corroborate it and for those who seek to disconfirm it. His theory of complexity prefigured the development of artificial intelligence.
Henri Poincaré had convinced his fellow mathematicians that the solar system is intrinsically unstable, and that uncertainty about the position of the planets, however small, makes any prediction of the position of the planets in the distant future impossible. But some seventy years later, in 1954, at the International Congress of Mathematicians in Amsterdam, Kolmogorov presented an astonishing result. Harnessing probabilities and the deterministic equations of mechanics with breathtaking audacity, he argued that the solar system
probably
is stable. Instability is possible, as Poincaré correctly saw—but if it occurs, it should occur only rarely.
Kolmogorov’s theorem asserts that if one assumes an exactly soluble mechanical system (in this case, the solar system as Kepler imagined it to be, with the planets endlessly revolving around the sun in regular and unchanging elliptical orbits), and if one then disturbs it ever so slightly (taking into account the gravitational force of attraction, neglected by Kepler), the resulting system remains stable for the great majority of initial conditions.
Kolmogorov’s argument was not widely accepted at first. This was mainly because of its complexity, but Kolmogorov’s own elliptical style of exposition didn’t help matters. Less than a decade later, however, the Russian mathematician Vladimir Arnold and the German mathematician Jürgen Moser, using different approaches, succeeded in providing a complete demonstration, Arnold proving Kolmogorov’s original statement of the theorem and Moser a more general variant of it. Thus was born KAM theory, which in its turn has given birth to some of the most powerful and surprising results in classical mechanics.

Andrei Kolmogorov
The singular beauty of this theory silenced skeptics, and for the next twenty-five years the solar system was believed to be stable, even if the technical constraints of Kolmogorov’s theorem did not correspond exactly to reality. With the work of the French astrophysicist Jacques Laskar in the late 1980s, however, opinion reversed itself once more. But that’s another story.…
Chaillol
April 15, 2008
The audience holds its breath, the teacher gives the cue, and the young musicians all at once make their bows dance across the strings.…
The Suzuki method requires parents to attend their children’s group lessons. Here, high in the French Alps, the lessons are given in a grand ski chalet. The main floor is entirely taken up by a stage and rows of seats. What else is there to do but watch—and listen?
We try not to grimace at the most grating noises. Those of us who volunteered yesterday to make fools of ourselves (to our children’s great delight) by playing their instruments know full well how difficult it is to make these diabolical contraptions produce the right sound! Today the atmosphere’s just right: the adults are in a good mood, the children are happy.
Suzuki method or no Suzuki method, what matters most of all is the teacher, and the one who is helping my son learn to play the cello is really, really talented.
Sitting toward the front, I find myself in almost the same position as my son—devouring Binney and Tremaine’s classic work,
Galactic Dynamics
, with the enthusiasm of a small child discovering a new world. I had no idea that the Vlasov equation was so important in astrophysics. Boltzmann’s is still the most beautiful equation in the world, but Vlasov’s isn’t too shabby!
Not only have I come to think better of the Vlasov equation, but all of a sudden the stars in the sky interest me more than they used to. Spiral galaxies and globular clusters always did seem pretty cool. But now that I have a mathematical key to unlock their secrets I find them completely and utterly fascinating.
Since my meeting with Clément three weeks ago I’ve gone over the calculations again, and now I’m starting to have some ideas of my own, mumbling to myself as I read Binney and Tremaine:
“Don’t get it, they say Landau damping is quite different from phase mixing.… But aren’t they basically the same thing?
Hrmrmrm
.”
A quick glance at the little blond darlings. They’re doing fine without me.
“Hmmmm, this calculation’s rather interesting. And what’s the note at the bottom of the page say?… the important thing in the linearized equation is not the spectral analysis, it’s the solution of the Cauchy problem. Well, yeah, I guess so—that’s common sense! Okay, let’s see how they do this … hmmmm … Fourier transform. Smart move, nothing beats good old Fourier’s method. Laplace transform, dispersion relation…”
I’m learning quickly, immersing myself in the stuff, absorbing it like a child soaking up a foreign language. Humbly, without pretending to know much of anything, I’m teaching myself basic concepts that physicists have known for half a century.…
* * *
In the evening I took a break from my studies. Sitting cross-legged in the attic bedroom of the small chalet where we’re staying, I devoured the latest collection of short stories by Neil Gaiman,
Fragile Things
—just out in paperback last fall, not yet translated into French. I believe Gaiman is right: we owe it to ourselves to tell stories. Like his tale of a brilliant improvisation on double bass. And of a very old, frail woman recalling her past loves. And of a phoenix that is always rising from its ashes and always being cooked and served for dinner …
Closed my eyes, finally, but couldn’t fall asleep. Couldn’t turn on the light, it’s just one room for the whole family. So my brain went haywire. Very old, frail galaxies improvised a story out of Gaiman, the problem kept coming back to life, only to end up being cooked by the mathematicians and served for dinner, over and over again. Stars sprouted inside my head. What exactly was that theorem I wanted to prove?
* * *
“Crawcrustle,” said Jackie Newhouse, aflame, “answer me truly. How long have you been eating the Phoenix?”
