Einstein and the Quantum (45 page)

Erwin Schrödinger (1887–1961): Austrian theoretical physicist and Nobel laureate (1933). He invented the wave equation approach to quantum mechanics, which is the main approach used in modern physics.

Duke Louis de Broglie (1892–1987): French theoretical physicist and Nobel laureate (1929). He proposed the idea of matter waves, the complement to Einstein's notion of quanta of light, and influenced Einstein's work on the quantum gas of atoms.

Max Born (1882–1970): German Jewish theoretical physicist and Nobel laureate (1954). He played a major role in formalizing the Heisenberg approach to quantum mechanics, known as matrix mechanics, as well as in providing the probabilistic interpretation of Schrödinger waves. He was one of Einstein's closest friends.

Werner Heisenberg (1901–1976): German theoretical physicist and Nobel laureate (1932). He invented the first correct formulation of modern quantum mechanics, matrix mechanics, in 1925. Two years later he proposed his uncertainty principle.

Wolfgang Pauli (1900–1958): Austrian theoretical physicist and Nobel laureate (1945). A brilliant but caustic personality, he discovered that electrons do not obey Bose statistics, because only one electron can occupy a given quantum state, the Pauli exclusion principle.

APPENDIX 2: THE THREE THERMAL RADIATION LAWS

OVERVIEW

All objects emit electromagnetic radiation because they contain some amount of thermal energy that excites some of their atoms and molecules, at any one time, to higher energy states. These excited atoms and molecules then emit radiation (photons) and fall back down to their lowest (ground) state, while others are continually being excited, which maintains energy balance (thermal equilibrium). The amount of thermal energy an object has increases with its temperature, and so it emits more energetic, higher-frequency radiation as its temperature increases. But thermal radiation, unlike radio waves or laser light, for example, is not emitted at a single frequency; it is emitted over a broad band of frequencies, with the most radiation coming out at a specific frequency (the “peak” of the radiation curve), which depends on the temperature.

The key question challenging physicists circa 1900 was how much energy in the form of radiation is emitted in each band of frequencies for a perfect emitter at a given temperature. Because of a principle of thermodynamics known as Kirchoff's law, a perfect emitter must also be a perfect absorber of radiation (i.e., a perfectly black object), called a blackbody, and the radiation it emits is called blackbody radiation. That doesn't necessarily mean it will appear black to the eye; if it is heated to a sufficiently high temperature, it will glow at optical frequencies, which are visible to the eye. Thus the holy grail for the physics of heat at the time was the determination of the universal mathematical formula describing the energy of heat radiation (per unit volume) in a given frequency band for a given temperature; we will call this formula “the thermal radiation law.” There were three radiations laws of historical importance.

1. The Planck law: This law was proposed and then derived by Max Planck in the fall of 1900, when it became clear that the Wien law failed. In order to justify this new law, Planck had to introduce the concept of quantization of energy (although he did not put it that way), which set the quantum revolution in motion. It required the introduction of Planck's constant,
h
, which appears in the radiation law and in the fundamental relation
ε
=
hυ
, relating the allowed increments of the energy,
E
, of a vibrating molecule to its frequency of vibration,
υ
. His law fit the experimental data very well and still does to this day. It is the correct radiation law according to modern physics.

2. The Wien law: This law was proposed by Wilhelm Wien in the early 1890s and was believed by many, including Planck, to be correct until 1900. It turns out to be an approximation to the correct Planck law that works well when one looks at frequencies that are higher than the peak frequency of the Planck law for a given temperature. For the achievable temperatures for blackbody experiments at the time of these first measurements, the higher frequencies were at or near the visible portion of the electromagnetic spectrum, and hence more easily measured, than those below the peak frequency, which were at infrared wavelengths.

3. The Rayleigh-Jeans law: A version of this law was proposed provisionally by Lord Rayleigh in 1900, and it turns out to be an approximation to the correct Planck law at low frequencies, that is, well below the peak frequency predicted by the Planck law. It was then proposed in its correct form by Rayleigh, with input from James Jean, in 1905; at roughly the same time it was derived but then rejected by Albert Einstein. Einstein rejected because it led to the “ultraviolet catastrophe.” This ominous descriptor was invented by the physicist Paul Ehrenfest because the Rayleigh-Jeans law predicts that the total energy in thermal radiation should be infinite. Einstein believed this property ruled out the law, whereas Jeans argued for a loophole that kept the theory in play until roughly 1911, when the Planck law became universally accepted.

MATHEMATICAL STATEMENT OF THE RADIATION LAWS

This section assumes that one knows the properties of the exponential function,
e
^x
. Here the letter
e
stands for the irrational number that is the base of the natural logarithm. The object to be calculated to describe thermal radiation is the so-called spectral energy density of radiation,
ρ
(
υ
,
T
), which describes the energy of radiation emitted by a blackbody in a small interval centered at frequency
υ
for an object at absolute temperature
T
. According to Planck the correct form of this function is

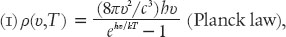
where
h
is Planck's constant,
k
is Boltzmann's constant, and
c
is the speed of light. Note that the factor in parentheses in the numerator is the one that Bose mentioned in his letter to Einstein in 1924, which contained his new derivation of the radiation law.

The exponential function gets very large compared to 1 when its argument, in this case the ratio
hυ
/
kT
, is larger than 1 (i.e., when
hυ
>
kT
). When this is the case, one can neglect the term –1 in the denominator of the Planck law, and one finds the approximate form of the radiation law

(2)
ρ
(
υ
,
T
) ≈ (8
πhυ
³
/
c
³
)
e
^{−
hυ
/
kT}
(Wien law).

This is the form of the radiation law proposed by Wilhem Wien, which we now know is a good approximation for frequencies
υ
>>
kT
/
h
. This defines what is meant by “high frequency”; it is a relative term, and it depends on the temperature of the blackbody. Visible light is considered high frequency at the temperature of the earth's surface but not at the temperature of the sun's surface.

In the other limit, of low frequencies, when the
υ
<<
kT
/
h
, the exponential function becomes close to the value 1. In fact e
^x
≈ 1 +
x
(here
x
stands for h
υ
/
kT
), and if we put this into equation (1) for the Planck law, a factor of
hυ
cancels in between the numerator and denominator, and with it all trace of the quantization of energy inherent in the Planck law vanishes. The resulting formula is

(3)
ρ
(
υ
,
T
) ≈ (8
πυ
²
/
c
³
)
kT
(Rayleigh-Jeans law).

Note that this approximation to the thermal radiation law shows that for a given frequency, the amount of energy is proportional to the temperature. This is the experimental clue that led Planck to the correct radiation law. However, for a given temperature the energy density is also proportional to the square of the frequency. If this were the correct radiation law for
all
frequencies, one would reach the absurd conclusion that the energy density for high frequencies tends to infinity. This is the ultraviolet catastrophe that Einstein objected to in 1905.

The graph in
figure A2.1
compares the three radiation laws.

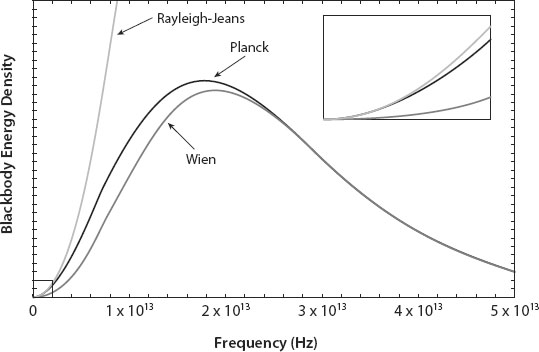
FIGURE A2.1.
Graph of the three proposed Radiation Laws, with energy density on the vertical axis and frequency on the horizontal axis, for a blackbody at room temperature. The lightest gray curve, which simply increases to infinity, is the Rayleigh-Jeans Law; note that it agrees with the Planck Law (black curve) for very low frequencies. The black curve is the Planck Law with a peak and then a decay, but with a more rapid rise at low frequencies than the Wien Law (gray). The Wien Law disagrees substantially with the Planck Law below the peak, but agrees very well with it above the peak. Inset is a blow up of the little dashed box in the graph at low frequencies, to show the excellent agreement between the Planck and Rayleigh-Jeans Law, and large disagreement with Wien's Law that was first found experimentally circa 1900. Courtsey of Alex Cerjan.

NOTES

BOOK EPIGRAPH

Page

vi
Science as something already in existence
: John Stachel, “Einstein and the Quantum,” in
Einstein from B to Z
, vol. 9 (Boston: Birkhauser, 2002), 373.

INTRODUCTION. A HUNDRED TIMES MORE THAN RELATIVITY THEORY

Page

3
I have thought a hundred times
: Abraham Pais,
Subtle Is the Lord
(Oxford: Oxford University Press, 2005), 9.

CHAPTER 1. “AN ACT OF DESPERATION”

Page

7
It would be edifying if
: Albert Einstein, “Max Planck as a Scientist,” in
The Collected Papers of Albert Einstein
, trans. Anna Beck (Princeton: Princeton University Press, 1987–2009), vol. 4, doc. 23, p. 273. All citations are to the English editions of the papers and will be abbreviated
CPAE
.

8
my decision to devote myself
: Max Planck,
Scientific Biography and Other Papers
, trans. Frank Gaynor (New York: Philosophical Library, 1949), 13.

10
the limits of validity
: Thomas Kuhn,
Black-Body Theory and the Quantum Discontinuity, 1894–1912
(Chicago: University of Chicago Press, 1978), 89.

10
the only physical theory
: P. A. Schilpp, ed.,
Albert Einstein: Philosopher-Scientist
(La Salle: Open Court, 1970), 33.

10
he is the model of the theorist
: Planck to Wien, 27 February 1909, in J. L. Heilbron,
Dilemmas of an Upright Man
:
Max Planck as Spokesman for German Science
(Berkeley: University of California Press, 1986), 8.

11
The interesting results of long wavelength
: Max Planck, “On an Improvement of Wien's Equation for the Spectrum” [original article no. 1 in References], reprinted in Haar,
The Old Quantum Theory
, 79.

11
by nature … peacefully inclined
: Planck to Robert William Woods, 7 October 1931, in Armin Hermann,
The Genesis of Quantum Theory (1899–1913)
(Cambridge, MA: MIT Press, 1971), 23.

12
I should therefore be permitted
: Planck, “On an Improvement,” 81.

12
even if the absolutely precise
: Planck,
Scientific Autobiography and Other Papers
(New York: Philosophical Library, 1949), 41.

12
some weeks of the most strenuous
: Max Planck, Nobel Lecture, p. 4,
http://nobelprize.org/physics/laureates/1918/planck-lecture.html
, accessed May 14, 2006.

12
We consider, however
: Max Planck, “On the Theory of the Energy Distribution Law of the Normal Spectrum” [original article no. 2 in References], reprinted in translation in Haar,
The Old Quantum Theory
, 84.