Gödel, Escher, Bach: An Eternal Golden Braid (102 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

general recursive function) exists which gives exactly the same answers as the sentient being's method does. Moreover: The mental process and the FlooP
program are isomorphic in the sense that on some level there is a correspondence between the steps being carried out in both computer and brain.
Notice that not only has the conclusion been strengthened, but also the proviso of communicability of the faint-hearted Public-Processes Version has been dropped. This bold version is the one which we now shall discuss.
In brief, this version asserts that when one computes something, one's mental activity can be mirrored isomorphically in some FlooP program. And let it be very clear that this does not mean that the brain is actually running a FlooP program, written in the FlooP language complete with
BEGIN's
,
END's
,
ABORT's
, and the rest-not at all. It is just that the steps are taken in the same order as they could be in a FlooP program, and the logical structure of the calculation can be mirrored in a FlooP program.
Now in order to make sense of this idea, we shall have to make some level distinctions in both computer and brain, for otherwise it could be misinterpreted as utter nonsense. Presumably the steps of the calculation going on inside a person's head are on the highest level, and are supported by lower levels, and eventually by hardware. So if we speak of an isomorphism, it means we've tacitly made the assumption that the highest level can be isolated, allowing us to discuss what goes on there independently of other levels, and then to map that top level into FlooP. To be more precise, the assumption is that there exist software entities which play the roles of various mathematical constructs, and which are activated in ways which can be mirrored exactly inside FlooP (see Fig.
106). What enables these software entities to come into existence is the entire infrastructure discussed in Chapters XI and XI I, as well as in the Prelude, Ant Fugue.
There is no assertion of isomorphic activity on the lower levels of brain and computer (e.g., neurons and bits).
The spirit of the Isomorphism Version, if not the letter, is gotten across by saying that what an idiot savant does in calculating, say, the logarithm of 7r, is isomorphic to what a pocket calculator does in calculating it-where the isomorphism holds on the arithmetic-step level, not on the lower levels of, in the one case, neurons, and in the other, integrated circuits. (Of course different routes can be followed in calculating anything-but presumably the pocket calculator, if not the human, could be instructed to calculate the answer in any specific manner.)
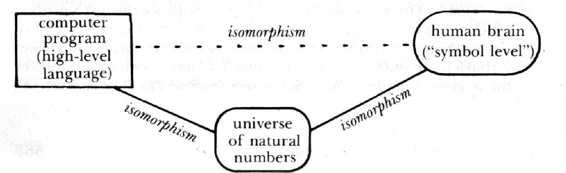
FIGURE 106.
The behavior of natural numbers can be mirrored in a human brain or in
the programs of a computer. These two different representations can then be mapped
onto each other on an appropriately abstract level.
Representation of Knowledge about the Real World
Now this seems quite plausible when the domain referred to is number theory, for there the total universe in which things happen is very small and clean. Its boundaries and residents and rules are well-defined, as in a hard-edged maze. Such a world is far less complicated than the open-ended and ill-defined world which we inhabit. A number theory problem, once stated, is complete in and of itself. A real-world problem, on the other hand, never is sealed off from any part of the world with absolute certainty. For instance, the task of replacing a burnt-out light bulb may turn out to require moving a garbage bag; this may unexpectedly cause the spilling of a box of pills, which then forces the floor to be swept so that the pet dog won't eat any of the spilled pills, etc., etc. The pills and the garbage and the dog and the light bulb are all quite distantly related parts of the world-yet an intimate connection is created by some everyday happenings. And there is no telling what else could be brought in by some other small variations on the expected. By contrast, if you are given a number theory problem, you never wind up having to consider extraneous things such as pills or dogs or bags of garbage or brooms in order to solve your problem. (Of course, your intuitive knowledge of such objects may serve you in good stead as you go about unconsciously trying to manufacture mental images to help you in visualizing the problem in geometrical terms-but that is another matter.)
Because of the complexity of the world, it is hard to imagine a little pocket calculator that can answer questions put to it when you press a few buttons bearing labels such as "dog", "garbage", "light bulb", and so forth. In fact, so far it has proven to be extremely complicated to have a full-size high-speed computer answer questions about what appear to us to be rather simple subdomains of the real world. It seems that a large amount of knowledge has to be taken into account in a highly integrated way for
"understanding" to take place. We can liken real-world thought processes to a tree whose visible part stands sturdily above ground but depends vitally on its invisible roots which extend way below ground, giving it stability and nourishment. In this case the roots symbolize complex processes which take place below the conscious level of the mind-processes whose effects permeate the way we think but of which we are unaware. These are the "triggering patterns of symbols" which were discussed in Chapters XI and XII.
Real-world thinking is quite different from what happens when we do a multiplication of two numbers, where everything is "above ground", so to speak, open to inspection. In arithmetic, the top level can be "skimmed off " and implemented equally well in many different sorts of hardware: mechanical adding machines, pocket calculators, large computers, people's brains, and so forth. This is what the Church-Turing Thesis is all about. But when it comes to real-world understanding, it seems that there is no simple way to skim off the top level, and program it. alone. The triggering patterns of symbols are just too complex. There must he several levels through which thoughts may "percolate" and "bubble".
In particular-and this comes back to a major theme of Chapters XI ' and XII-the representation of the real world in the brain, although rooted in isomorphism to some extent, involves some elements which have no counterparts at all in the outer world. That is, there is much more to it than simple mental structures representing "dog", "broom", etc. All of these symbols exist, to be sure-but their internal structures are extremely complex and to a large degree are unavailable for conscious inspection. Moreover, one would hunt in vain to map each aspect of a symbol's internal structure onto some specific feature of the real world.
Processes That Are Not So Skimmable
For this reason, the brain begins to look like a very peculiar formal system, for on its bottom level-the neural level-where the "rules" operate and change the state, there may be no interpretation of the primitive elements (neural firings, or perhaps even lower-level events). Yet on the top level, there emerges a meaningful interpretation-a mapping from the large "clouds" of neural activity which we have been calling "symbols", onto the real world. There is some resemblance to the Gödel construction, in that a high-level isomorphism allows a high level of meaning to be read into strings; but in the Gödel construction, the higher-level meaning "rides" on the lower level-that is, it is derived from the lower level, once the notion of Gödel-numbering has been introduced. But in the brain, the events on the neural level are not subject to real-world interpretation; they are simply not imitating anything. They are there purely as the substrate to support the higher level, much as transistors in a pocket calculator are there purely to support its number-mirroring activity. And the implication is that there is no way to skim off just the highest level and make an isomorphic copy in a program; if one is to mirror the brain processes which allow real-world understanding, then one must mirror some of the lower-level things which are taking place: the "languages of the brain". This doesn't necessarily mean that one must go all the way down to the level of the hardware, though that may turn out to be the case.
In the course of developing a program with the aim of achieving an "intelligent"
(viz., human-like) internal representation of what is "out there", at some point one will probably be forced into using structures and processes which do not admit of any straightforward interpretations-that is, which cannot be directly mapped onto elements of reality. These lower layers of the program will be able to be understood only by virtue of their catalytic relation to layers above them, rather than because of some direct connection they have to the outer world. (A concrete image of this idea was suggested by the Anteater in the Ant Fugue: the "indescribably boring nightmare" of trying to understand a book on the letter level.)
Personally, I would guess that such multilevel architecture of concept-handling systems becomes necessary just when processes involving images and analogies become significant elements of the program-in
contrast to processes which are supposed to carry out strictly deductive reasoning.
Processes which carry out deductive reasoning can be programmed in essentially one single level, and are therefore skimmable, by definition. According to my hypothesis, then, imagery and analogical thought processes intrinsically require several layers of substrate and are therefore intrinsically non-skimmable. I believe furthermore that it is precisely at this same point that creativity starts to emerge-which would imply that creativity intrinsically depends upon certain kinds of "uninterpretable" lower-level events. The layers of underpinning of analogical thinking are, of course, of extreme interest, and. some speculations on their nature will be offered in the next two Chapters.
Articles of Reductionistic Faith
One way to think about the relation between higher and lower levels in the brain is this.
One could assemble a neural net which, on a local (neuron-to-neuron) level, performed in a manner indistinguishable from a neural net in a brain, but which had no higher-level meaning at all. The fact that the lower level is composed of interacting neurons does not necessarily force any higher level of meaning to appear-no more than the fact that alphabet soup contains letters forces meaningful sentences to be found, swimming about in the bowl. High-level meaning is an optional feature of a neural network-one which may emerge as a consequence of evolutionary environmental pressures.
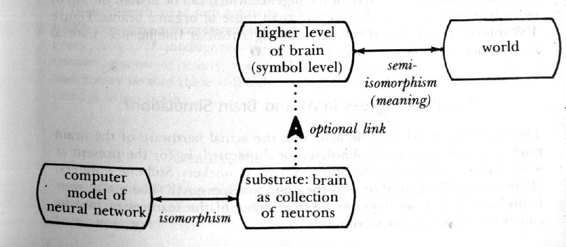
Figure 107 is a diagram illustrating the fact that emergence of a higher level of meaning is optional. The upwards-pointing arrow indicates that a substrate can occur without a higher level of meaning, but not vice versa: the higher level must be derived from properties of a lower one.
FIGURE 107.
Floating on neural activity, the symbol level of the brain mirrors the
world. But neural activity per se, which can be simulated on a computer, does not create
thought; that calls for higher levels of organization
.
The diagram includes an indication of a computer simulation of a neural network. This is in principle feasible, no matter how complicated the network, provided that the behavior of individual neurons can be described in terms of computations which a computer can carry out. This is a subtle postulate which few people even think of questioning.
