Gödel, Escher, Bach: An Eternal Golden Braid (105 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

"semantic" properties are connected to open-ended searches because, in an important sense, an object's
meaning is not localized
within the object itself. This is not to say that no understanding of any object's meaning is possible until the end of time, for as time passes, more and more of the meaning unfolds. However, there are always aspects of its meaning which will remain hidden arbitrarily long.
Meaning Derives from Connections to Cognitive Structures
Let us switch from strings to pieces of music, just for variety. You may still substitute the term "string" for every reference to a piece of music, if you prefer.
The discussion is meant to be general, but its flavor is better gotten across, I feel, by referring to music. There is a strange duality about the meaning of a piece of music: on the one hand, it seems to be spread around, by virtue of its relation to many other things in the world-and yet, on the other hand, the meaning of a piece of music is obviously derived from the music itself, so it must be localized somewhere inside the music.
The resolution of this dilemma comes from thinking about the interpreter-the mechanism which does the pulling-out of meaning. (By "inter
preter in this context, I mean not -the performer of the piece, but the mental mechanism in the listener which derives meaning when the piece is played.) The interpreter may discover many important aspects of a piece's meaning while hearing it for the first time; this seems to confirm the notion that the meaning is housed in the piece itself, and is simply being read off. But that is only part of the story. The music interpreter works by setting up a multidimensional cognitive structure-a mental representation of *_he piece-which it tries to integrate with pre-existent information by finding links to other multidimensional mental structures which encode previous experiences. As this process takes place, the full meaning gradually unfolds. In fact, years may pass before someone comes to feel that he has penetrated to the core meaning of a piece. This seems to support the opposite view: that musical meaning is spread around, the interpreter's role being to assemble it gradually.
The truth undoubtedly lies somewhere in between: meanings-both musical and linguistic-are to some extent localizable, to some extent spread around. In the terminology of Chapter VI, we can say that musical pieces and pieces of text are partly triggers, and partly carriers of explicit meaning. A vivid illustration of this dualism of meaning is provided by the example of a tablet with an ancient inscription: the meaning is partially stored in the libraries and the brains of scholars around the world, and yet it is also obviously implicit in the tablet itself.
Thus, another way of characterizing the difference between "syntactic" and
"semantic" properties (in the just-proposed sense) is that the syntactic ones reside unambiguously inside the object under consideration, whereas semantic properties depend on its relations with a potentially infinite class of other objects, and therefore are not completely localizable. There is nothing cryptic or hidden, in principle, in syntactic properties, whereas hiddenness is of the essence in semantic properties. That is the reason for my suggested distinction between "syntactic" and "semantic" aspects of visual form.
Beauty, Truth, and Form
What about beauty? It is certainly not a syntactic property, according to the ideas above.
Is it even a semantic property? Is beauty a property which, for instance, a particular painting has? Let us immediately restrict our consideration to a single viewer. Everyone has had the experience of finding something beautiful at one time, dull another time-and probably intermediate at other times. So is beauty an attribute which varies in time? One could turn things around and say that it is the beholder who has varied in time. Given a particular beholder of a particular painting at a particular time, is it reasonable to assert that beauty is a quality that is definitely present or absent? Or is there still something ill-defined and intangible about it?
Different levels of interpreter probably could be invoked in every person, depending on the circumstances. These various interpreters pull out different meanings, establish different connections, and generally evaluate all deep aspects differently. So it seems that this notion of beauty is extremely hard to pin down. It is for this reason that I chose to link beauty, in the Magnificrab, with truth, which we have seen is also one of the most intangible notions in all of metamathematics.
The Neural Substrate of the Epimenides Paradox
I would like to conclude this Chapter with some ideas about that central problem of truth, the Epimenides paradox. I think the Tarski reproduction of the Epimenides paradox inside TNT points the way to a deeper understanding of the nature of the Epimenides paradox in English. What Tarski found was that his version of the paradox has two distinct levels to it. On one level, it is a sentence about itself which would be true if it were false, and false if it were true. On the other level-which I like to call the arithmetical substrate-it is a sentence about integers which is true if and only if false.
Now for some reason this latter bothers people a lot more than the former. Some people simply shrug off the former as "meaningless", because of its self-referentiality.
But you can't shrug off paradoxical statements about integers. Statements about integers simply cannot be both true and false.
Now my feeling is that the Tarski transformation of the Epimenides paradox teaches us to look for a substrate in the English-language version. In the arithmetical version, the upper level of meaning is supported by the lower arithmetical level. Perhaps analogously, the self-referential sentence which we perceive ("This sentence is false") is only the top level of a dual-level entity. What would be the lower level, then? Well, what is the mechanism that language rides on? The brain. Therefore one ought to look for a neural substrate to the Epimenides paradox-a lower level of physical events which clash with each other. That is, two events which by their nature cannot occur simultaneously. If this physical substrate exists, then the reason we cannot make heads or tails of the Epimenides sentence is that our brains are trying to do an impossible task.
Now what would be the nature of the conflicting physical events? Presumably when you hear the Epimenides sentence, your brain sets up some "coding" of the sentence-an internal configuration of interacting symbols. Then it tries to classify the sentence as "true" or "false". This classifying act must involve an attempt to force several symbols to interact in a particular way. (Presumably this happens when any sentence is processed.) Now if it happens that the act of classification would physically disrupt the coding of the sentence-something which would ordinarily never happen-then one is in trouble, for it is tantamount to trying to force a record player to play its self-breaking record. We have described the conflict in physical terms, but not in neural terms. If this analysis is right so
far, then presumably the rest of the discussion could be carried on when we know •
something about the constitution of the "symbols" in the brain out of neurons and their firings, as well as about the way that sentences become converted into "codings".
This sketch of the neural substrate of the Epimenides paradox suggests (to me, at least) that the resolution of the English version of the Epimenides paradox might be similar to that for the Tarski version. The resolution involves abandoning the notion that a brain could ever provide a fully accurate representation for the notion of truth. The novelty of this resolution lies in its suggestion that a total modeling of truth is impossible for quite physical reasons: namely, such a modeling would require physically incompatible events to occur in a brain.
SHRDLU
,
Toy of Man's Designing
One day, Eta Oin wanders into the MIT Artificial Intelligence Laboratory,
where she runs into the brilliant young computer program, SHRDLU. It
happens that SHRDLU is just dying for someone to try out the newly
developed human being "Dr. Tony Earrwig". SHRDLU explains that this
Earrwig is fairly intelligent in the limited domain of analyzing a conversation
about a "toy world" containing blocks of various shapes, sizes, and colors-blocks which sit on a table, and which can be picked up and moved around.
Eta Oin, fascinated, begins enthusiastically typing to SHRDLU. Earrwig
dangles over her shoulder and provides a sort of running commentary, as
promised.
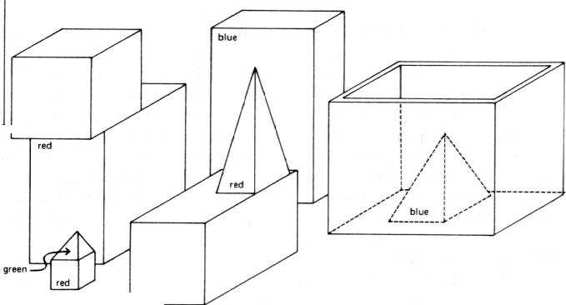
1. Eta Oin: pick up a big red block. [Refer to Fig. 110.
SHRDLU: OK.
Dr. Tony Earrwig: SHRDLU answers "OK" when it carries out a command. In order
to pick up the red block, it had to clear it off by finding a space for the green one
and moving the green one away.
2. Eta Oin: grasp the pyramid.
SHRDLU: I DON'T UNDERSTAND WHICH PYRAMID YOU MEAN.
Dr. Tony Earrwig: There are three pyramids in the scene, and SHRDLU knows that
phrases beginning with "the" are intended to refer to a specific object the speaker has in
mind.
FIGURE 110
. "Pick up a big red block." [From Terry Winograd, Understanding Natural
Language, (New York: Academic Press, 1972), p. 8.1
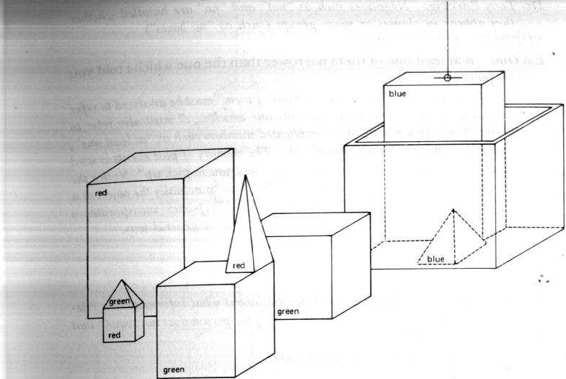
FIGURE 111. "
Find a block which is bigger than the one you are holding and put it into the
box." Adapted from Terry Winograd, Understanding Natural Language, p.9.]
3. Eta Oin: find a block which is taller than the one you are holding and put it into the box.
[Refer to Fig. 111.]
Dr. Tony Earrwig: SHRDLU has to figure out what is meant by "one" and "it", as well as
using deduction to decide which block it is holding.
SHRDLU: BY "IT", I ASSUME YOU MEAN THE BLOCK WHICH IS TALLER
THAN THE ONE I AM HOLDING.
Dr. Tony Earrwig: There were two possible referents for "it": the one selected, and "the
one you are holding". SHRDLU has heuristics for choosing between them.
SHRDLU: OK.
Dr. Tony Earrwig: SHRDLU's hand has to set down the red block pick up the taller blue
one.
Eta Oin: what does the box contain?
SHRDLU: THE BLUE PYRAMID AND THE BLUE BLOCK.
Eta Oin: what is the pyramid supported by?
Dr. Tony Earrwig: Earlier SHRDLU responded to "the pyramid" by saying "I DON'T
UNDERSTAND WHICH PYRAMID YOU MEAN." Now, it assumes that you mean the
one just mentioned.
SHRDLU: THE BOX.
Eta Oin: how many blocks are not in the box?
Dr. Tony Earrwig:
Negatives such as "not" and "no" are handled whether they appear in
clauses or noun groups (such as "no boxes")
.
SHRDLU: FOUR OF THEM.
7. Eta Oin: is at least one of them narrower than the one which i told you to pick up?
Dr. Tony Earrwig: The phrase "at least one of them" must be analyzed to refer
back to the previous question, and "the one which ..." must also refer to blocks.
Noun groups can have complicated numbers such as "at least one", "more than
three", "exactly seven", etc.. The memory of past events is used to deduce which
block is "the one which I told you to pick up". Notice the complicated syntactic
structure in which "the one" is actually the object of a clause embedded two levels
deeper. SHRDLU's parser incorporates a grammar that handles this kind of
complexity in a general way.
