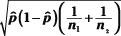Statistics Essentials For Dummies (38 page)

4.
Calculate the standard error:
5. Divide your result from Step 2 by your result from Step 4.
To interpret the test statistic, look up your test statistic on the standard normal distribution (Table A-1 in the appendix) and calculate the
p
-value.
For example the maker of Adderall, a drug for attention deficit hyperactivity disorder (ADHD), reported that 26 of the 374 subjects (7%) who took the drug experienced vomiting as a side effect, compared to 8 of the 210 subjects (4%) who were on a
placebo
(fake drug). Note that patients didn't know which treatment they were given. In the sample, more people on the drug experienced vomiting, but is this percentage enough to say that the entire population would experience more vomiting? You can test it to see. In this case you have H
o
:
p
1
-
p
2
= 0 versus H
a
:
p
1
-
p
2
> 0, where
p
1
represents the proportion of subjects who vomited using Adderall, and
p
2
represents the proportion of subjects who vomited using the placebo.
Why does H
a
contain a ">" sign and not a "<" sign? H
a
represents the scenario in which those taking Adderall experience more vomiting than those on placebo — that's something the FDA would want to know about.
The next step is calculating the test statistic. First,
1
= 26/374 = 0.07 and2
= 8/210 = 0.04. The sample sizes are
n
1
= 374 and
n
2
= 210, respectively. Next, take the difference between these sample proportions to get 0.07 - 0.04 = 0.03. The overall sample proportion,, is (26 + 8)/(374 + 210) = 34/584 = 0.058. The
standard error is
= 0.02. Finally,
take the difference from Step 2, 0.03, divided by 0.02 to get 0.03/0.02 = 1.5, which is the test statistic.
The
p
-value is the percentage chance of being at or beyond (in this case to the right of) 1.5, which is 100% - 93.32% = 6.68%, which is written as a probability as 0.0668. This
p
-value is greater than 0.05, so you don't have enough evidence to reject H
o
. That means vomiting is not experienced any more by those taking this drug when compared to a placebo.
You Could Be Wrong: Errors in Hypothesis Testing
After you decide whether to reject H
o
, the next step is living with the consequences — after all, you could be wrong.
If you conclude that a claim isn't true but it actually
is
true, a lawsuit, fine, unnecessary changes in the product, or consumer boycotts that shouldn't have happened could result.
If you conclude that a claim is true but it actually isn't, what happens then? Undetected problems will continue and no action will be taken. Inaction has consequences as well.
Rejecting H
o
when you shouldn't is called a
Type-1 error.
I don't really like this name, because it seems so nondescript. I prefer to call a Type-1 error a
false alarm.
In the case of the packages, if the consumer group made a Type-1 error when it rejected the company's claim, they created a false alarm. What's the result? A very angry delivery company.
A false alarm: Type-1 error
Suppose a company claims that its average package delivery time is 2 days, and a consumer group tests this hypothesis and concludes that the claim is false: They believe that the average delivery time is actually more than 2 days. This is a big deal. If the group can stand by its statistics, it has done well to inform the public about the false advertising issue. But what if the group is wrong? Even if the study is based on a good design, collects good data, and makes the right analysis, the group can still be wrong.
Why? Because its conclusions were based on a sample of packages, not on the entire population. As Chapter 6 tells you, sample results vary from sample to sample. If your test statistic falls on the tail of the standard normal distribution, these results are unusual, if the claim is true, because you expect them to be much closer to the middle of the standard normal distribution (
Z
-distribution). Just because the results from a sample are unusual, however, doesn't mean they're impossible. A
p
-value of 0.04 means that the chance of getting your particular test statistic (out on the tail of the standard normal distribution), even if the claim is true, is 4% (less than 5%). That's why you reject H
o
in this case, because that chance is so small. But a chance is a chance!