Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (19 page)

4.
Ask your students to compare the areas by tiling and multiplying. (Both are 15 square inches.)

5.
Now pose this problem: Mrs. Williams is planning to change her kitchen floor. She needs to buy 1-foot square tiles to cover the floor, which is 9 feet by 10 feet. What is the area of the floor? (90 square feet) How many tiles does she need? (90)

Closure

Ask your students questions such as the following: Does multiplying the length times the width of a rectangle always result in the area of a rectangle? (Students should realize this is true, because the width represents the number of rows, and the length represents the number of squares in each row. The product shows the number of squares needed to tile the rectangle, which is the number of square units.) Is finding the area of a rectangle by multiplying its length by its width easier than counting tiles? Ask your students to explain their answers.

Activity 2: Decomposing Areas

Working in pairs or groups of three, students will decompose area models to represent the distributive property.

Materials

Graph paper; reproducible, “The Area of the Sums,” for each pair or group of students.

Procedure

1.
Explain that rectangles can be decomposed (separated) into smaller rectangles. The area of the original rectangle is equal to the sum of the areas of smaller rectangles.

2.
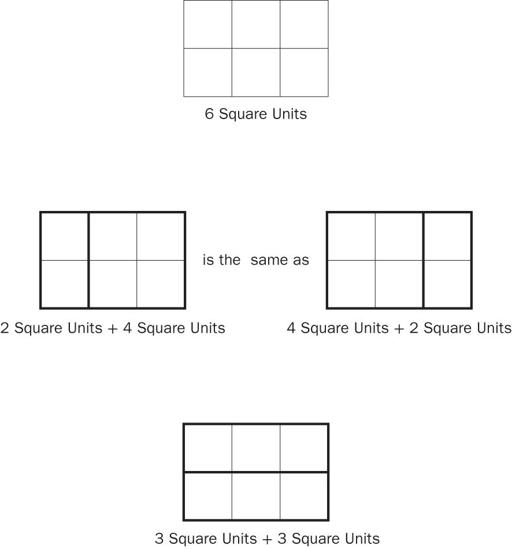
Distribute copies of the reproducible. Explain that at the top is a rectangle whose area is 6 square units. Below it are two different ways to decompose the rectangle into two smaller rectangles. (
Note:
If students point out that in the first example the original rectangle is decomposed into a rectangle and a square, remind them that a square is a special type of rectangle.)

3.
Instruct your students to draw a rectangle that has two rows, each with five squares, on their graph paper.

4.
Instruct them to decompose this rectangle into two smaller rectangles and find the area of each pair. There are three ways to do this. They should find all three.

Closure

Discuss the ways the rectangle can be decomposed. Ask your students: Do you think the sum of the areas of the smaller rectangles will always equal the area of the original rectangle? Why?

Answers

There are three ways to decompose the rectangle: a 2-by-1 and a 2-by-4 rectangle; a 2-by-2 and a 2-by-3 rectangle; a pair of 1-by-5 rectangles.

The Area of the Sums

Measurement and Data: 3.MD.8

“Geometric measurement: recognize perimeter as an attribute of plane figures and distinguish between linear and area measures.”

8. “Solve real-world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.”

Background

While the area of a polygon (a closed plane figure whose sides are line segments) is the number of square units needed to cover the flat surface, the perimeter of a polygon is the distance around the figure.

Two rectangles may have the same area but different perimeters. For example, a 4-by-5 rectangle and a 2-by-10 rectangle both have an area of 20 square units, but the perimeters are 18 units and 24 units respectively.

Two rectangles may have the same perimeters but different areas. For example, a 1-by-6 rectangle and a 3-by-4 rectangle both have a perimeter of 14 units, but their areas are 6 square units and 12 square units respectively.

Activity 1: Area and Finding Perimeter

Working in pairs or groups of three, students will create rectangles with a given area and then find the perimeters.

Materials

About 15 1-inch square color tiles; rulers; unlined paper; reproducible, “Areas and Perimeters of Rectangles,” for each pair or group of students.

Procedure

1.
Explain that rectangles may have the same area but different perimeters. Sketch a 4-by-5 rectangle and a 2-by-10 rectangle on the board. Both have an area of 20 square units, but their perimeters are 18 units and 24 units.

2.
Hand out copies of the reproducible. Explain that it contains instructions for creating rectangles that have a given area.

3.
Explain that students are to first use their tiles to create the rectangles, working with one rectangle at a time. After they create a rectangle, they are to draw it on their unlined paper, label each side, and find its perimeter. Be sure that students understand that a 1-by-2 rectangle, for example, is the same as a 2-by-1 rectangle. It is only positioned differently. In cases where there is more than one possible rectangle, students should provide drawings and perimeters for all of them. (If necessary, remind your students that a square is a special kind of rectangle.)

Closure

Discuss students' sketches and perimeters. Ask: How did you find the perimeters of the rectangles when given the areas?

Answers

The dimensions of the rectangles and their perimeters are listed in order.
(1)
1 by 1, 4.
(2)
1 by 2, 6.
(3)
1 by 4, 10; 2 by 2, 8.
(4)
1 by 5, 12.
(5)
1 by 8, 18; 2 by 4, 12.
(6)
1 by 9, 20; 3 by 3, 12.
(7)
1 by 10, 22; 2 by 5, 14.
(8)
1 by 12, 26; 2 by 6, 16; 3 by 4, 14

Activity 2: Perimeter and Finding Area

Working in pairs or groups of three, students will create rectangles with a given perimeter and then find the areas of the rectangles they created.

Materials

About 20 1-inch square color tiles; rulers; unlined paper; reproducible, “Perimeters and Areas of Rectangles,” for each pair or group of students.

Procedure

1.
Explain that rectangles may have the same perimeter but different areas. Sketch a 1-by-6 rectangle and a 3-by-4 rectangle on the board. Both have perimeters of 14 units but their areas are 6 square units and 12 square units.

2.
Hand out copies of the reproducible. Explain that it contains instructions for creating rectangles that have a given perimeter.

3.
Explain that students are to use their tiles to create rectangles that have the given perimeters, working with one rectangle at a time. After they create a rectangle, they are to draw it on their unlined paper, label its sides, and find its area. Be sure that students understand that a 1-by-2 rectangle, for example, is the same as a 2-by-1 rectangle. It is only positioned differently. In cases where there is more than one possible rectangle, students should provide drawings and areas for all of them. (If necessary, remind your students that a square is a special kind of rectangle.)

Closure

Discuss students' sketches and areas. Ask: How did you find the dimensions of the rectangles when given the perimeters?

Answers

The dimensions of the rectangles and the areas are listed in order.
(1)
1 by 1, 1.
(2)
1 by 2, 2.
(3)
1 by 4, 4; 2 by 3, 6.
(4)
1 by 5, 5; 2 by 4, 8; 3 by 3, 9.
(5)
1 by 7, 7; 2 by 6, 12; 3 by 5, 15; 4 by 4, 16

Activity 3: Designing a Vegetable Garden

Working in small groups, students will design a vegetable garden with a given perimeter. They will then find the area of their garden.

Materials

Graph paper; rulers for each group.

Procedure

1.
Explain that students are to design a vegetable garden. Because small animals, such as rabbits, like vegetables, students will need to place a wire fence around their garden. They have 50 feet of wire fence.

2.
Explain that students should design a rectangular garden with a perimeter of 50 feet. They should consider and sketch several possible plans before choosing the one they want.