The Clockwork Universe (13 page)
Read The Clockwork Universe Online
Authors: Edward Dolnick

For the Greeks, the word
mathematics
had vastly different associations than it does for most of us. Mathematics had almost nothing to do with adding up columns of numbers or figuring out how long it would take Bob and Tom working together to paint a room. The aim of mathematics was to find eternal truthsâinsights into the abstract architecture of the worldâand then to prove their validity. “A mathematician, like a painter or poet, is a maker of patterns,” wrote G. H. Hardy, an acclaimed twentieth-century mathematician and an ardent proponent of the Greek view. “If his patterns are more permanent than theirs, it is because they are made with ideas.”
Let's take a few minutes to look at the kind of thing Greek mathematicians accomplished, because it was their exampleâand the way they interpreted their successâthat inspired their intellectual descendants in the seventeenth century. (One of Newton's assistants could recall only one occasion when he had seen Newton laugh. Someone had made the mistake of asking Newton what use it was to study Euclid, “upon which Sir Isaac was very merry.”) The Greeks had looked for their “permanent patterns” in the world of mathematics. Seventeenth-century scientists set out with the same goal except that they expanded their quest to the world at large.
They found mathematics on all sides. When Isaac Newton directed a beam of light through a prism, he marveled at the rainbow on his wall. No one could miss either the beauty or the order in that familiar spectacle, but it was the interplay between the two that so intrigued Newton. “A naturalist would scarce expect to see ye science of those colours become mathematicall,” he wrote, “and yet I dare affirm that there is as much certainty in it as in any other part of Opticks.”
For the Greeks the notion of “proof”ânot a claim or a likelihood but actual proof beyond a doubtâwas fundamental. A proof in mathematics is a demonstration or an argument. It starts with assumptions and moves, step by step, to a conclusion. But unlike ordinary argumentsâwho was the greatest president? who makes the best pizza in Brooklyn?âmathematical arguments yield irrefutable, permanent, universally acknowledged truths.
Of all the shapes you can make with a piece of string
,
a circle encloses the biggest area.
The list of prime numbers never ends.
29
If three points aren't in a straight line
,
there is a circle that passes through all three.
Everyone who can follow the argument sees that it must be so.
Like other arguments, proofs come in many varieties. Mathematicians have individual, recognizable styles, just as composers and painters and tennis players do. Some think in pictures, others in numbers and symbols. The Greeks preferred to think pictorially. Take the Pythagorean theorem, for instance, perhaps the most famous theorem of them all. The theorem involves a right triangleâa triangle where one angle is 90 degreesâand relates the lengths of the various sides. In the simplest right triangle, one side is 3, another 4, and the longest 5. Many centuries before the birth of Christ, some unknown genius stared at those numbersâ3, 4, 5âand saw something that astonished him.
It's easy to draw a triangle with a side 3 inches long and a side 4 inches long and a third side that's short (at left, below), or a triangle with a side 3 inches long and a side 4 inches long and a third side that's long (at right, below). But if the angle between the 3-inch side and the 4-inch one is not just any angle but 90 degrees, then the length of the third side turns out to be precisely 5. So the puzzle pieces that our unknown genius turned over and over in his mind were these: 3, 4, 5, 90 degrees. What tied those numbers together?

No doubt he drew endless right triangles and measured the sides. Nearly always the longest side would be a seemingly random number, no matter how carefully the two short sides were chosen. Even in the simplest caseâa triangle where the two short sides were both 1 inch longâthe third side didn't look simple at all. A shade more than 1
â
inches, not even anything that lined up with the divisions on a ruler.
Perhaps he stuck with his experiments long enough to draw the right triangle with short sides 5 and 12. Set a ruler in place to draw the third side and then measure it. Success at lastâthe
long side is precisely 13 inches long, so here is another right
triangle with all three sides respectable whole numbers.
Two right triangles, two sets of numbers, like two words from a coded message. First set: 3, 4, 5. Second set: 5, 12, 13. What do the two triplets have in common?
For two thousand years, we have called the answer the Py
thagorean theoremâthe length of one short side, squared, plus
the other short side, squared, equals the long side, squared.
3
2
+ 4
2
= 5
2
. For the second triangle, 5
2
+ 12
2
= 13
2
.
30
More to the point, the relationship holds for
every
right triangle what
soever, whether it is scratched in the sand or splayed across the heavens.
31
In modern terms, the theorem is usually written as a
2
+ b
2
= c
2
. In the pictorial terms the Greeks preferred, the theorem is about squares, not numbers, and Pythagoras's claim is that the area of one small square added to the area of the other small square is exactly the same as the area of the large square. (See drawing below.) The two approaches, numerical and pictorial, are exactly equivalent. The choice between them is purely a matter of taste, like the choice between an architectural drawing and a scale model.
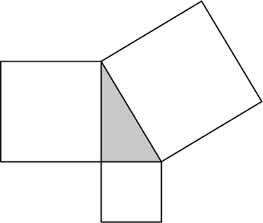
Pythagoras's theorem says that the area of one small square plus the area of the other small square is exactly equal to the area of the large square.
If you had somehow happened to guess the Pythagorean theorem, how would you prove it? It's not enough to draw a right triangle, measure the sides, and do the arithmetic. That would only serve to verify the theorem for one example, not for
all
right triangles. Moreover, not even the most careful measuring could confirm that the sum worked out precisely, to the millionth decimal point and beyond, as it must. But even a dozen successful examples, or a hundred, or a thousand, would still fall short of proof. “True beyond a reasonable doubt” applies in law and in ordinary lifeâwho doubts that the sun will rise tomorrow?âbut the Greeks demanded more.
Here is one classic proof, which proceeds in jigsaw-puzzle fashion and almost wordlessly. In math as in chess, crucial moves often look mysterious at the time. Why move a knight
there
when all the action is
here
? In this case, the unexpected move that brings the answer in reach is this: take the original triangle and make three identical copies of it, so that you have four triangles all exactly the same.
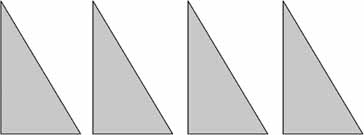
What's the gain in dealing with four triangles when we weren't sure what to do with one? The gain comes in imagining the triangles as cardboard cutouts and then sliding them around on a table in different arrangements. Look at Figure X and Figure Y
below. Two different arrangements, both with the same four
triangles and some white space. In both cases, the outlines (in bold) look like squares. How do we know they really are squares and not just four-sided, squarish shapes?
Stare at Figure X and Figure Y for a few seconds. All the bold sides are the same length (because each bold side is made up of a long side of the original triangle and a short side). And all the corners are right angles. So the bold shape in Figure X is a square, and so is the bold shape in Figure Y, and both squares are precisely the same size.
Almost done. Each bold square encloses the same area. Each
bold square is made up of four identical triangles and some white
space. Stare at the pictures again. The large white square in Figure X
has to be
exactly the same in area as the two smaller white squares in Figure Y. Voilà , we have Pythagoras!
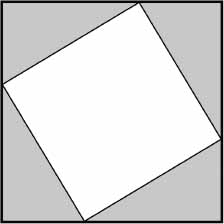
Figure X
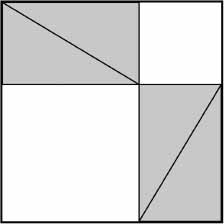
Figure Y
Why did the Greeks find that discovery so astonishing? Not for its utility. No Greek would have asked, “What good is it?” What good is a poem or a play? Would a sculpture be more admirable if it could also serve as a doorstop? Mathematics was true and it was beautiful, and that was more than enough. The point was not to find the length of a diagonal across a rectangular field without having to measure it, although the Pythagorean theorem lets you do that. The Greeks had loftier goals.
The Pythagorean theorem thrilled the Greeks for two reasons.
First, simply by thinkingâwithout using any tools whatsoeverâthey had discovered one of nature's secrets, an eternal and never-
before-suspected truth about the structure of the world. Second, they could prove it. Unlike nearly any other valid observationâ
vinegar is tart, Athens is dusty, Socrates is shortâthis particular
observation was not only true but
necessarily
true. One of God's thoughts, finally grasped by man.
Like all the best insights, it is simultaneously inevitable and surprising. But it may also be surprising that the Greeks took for granted that their mathematical theorems were facts
about the world
rather than man-made creations like houses or songs. Is mathematics invented or discovered? The Greeks came down emphatically in favor of “discovered,” but the question is ancient, like
what is justice?
and apparently just as difficult to resolve.
On the one hand, what could more plainly be human inventions
than the concepts of geometry and algebra? Even the simplest mathematical notion has no tangible existence in the everyday world. Who goes for a walk and trips over a 3? On the other hand, what could be more obvious than that the truths of mathematics are facts about the world, whether or not any humans catch on to them? If two dinosaurs were at a watering hole and two more dinosaurs came along to join them, the science writer Martin Gardner once asked, weren't there four dinosaurs altogether? Didn't three stars in the sky form a triangle before the first humans came along to define triangles
?
32
Newton and the other scientists of the seventeenth century shared the Greek view, and they coupled it with their own fundamental belief that the world was a cosmic code, a riddle designed by God. Their mission, in the words of one prominent writer of the day, was to decode that “strange Cryptography.” The Greeks had harbored similar ambitions, but the new scientists had advantages their predecessors had lacked. First, they had no taboos about studying motion mathematically. Second, they had calculus, a gleaming new weapon in the mathematical arsenal, to study it with.
Just as important, they had complete, unbreakable faith that the riddle had an answer. That was vital. No one would stick with a crossword puzzle if they feared that the areas of order might be mixed with patches of gibberish. Nature presented a greater challenge than any crossword, and only the certain knowledge that God had played fair kept scientists struggling year after year to catch on to His game.
Even so, the task was enormously difficult. Nonmathematicians underestimated the challenge. When Francis Bacon spoke of the mysteries of science, for instance, he made it sound as if God had set up an Easter egg hunt to entertain a pack of toddlers. God “took delight to hide his works, to the end to have them found out.”
Why would God operate in such a roundabout way? If his intent was to proclaim His majesty, why not arrange the stars to spell out
BEHOLD
in blazing letters? To seventeenth-century thinkers, this was no mystery. God
could
have put on a display of cosmic fireworks, but that would have been to win us over by shock and fear. When it came to intellectual questions, coercion was the wrong tool. Having created human beings and endowed us with the power of reason, God surely meant for us to exercise our gifts.
The mission of science was to honor God, and the best way to pay Him homage was to discover and proclaim the perfection of His plans.
