The Clockwork Universe (15 page)
Read The Clockwork Universe Online
Authors: Edward Dolnick

Kepler believed that God had arranged the planets' orbits according to this geometric scheme. (For clarity, the diagram shows only the four outermost planets, not all six planets known in Kepler's day.)
Johannes Kepler had discovered the architecture of the solar system. Or so he believed, and in his fever dream he filled sheet
after sheet with ever more elaborate geometric diagrams. For the young, unknown astronomer, this was dizzyingly exciting. Without looking out the window, he had not only assigned each planet
to its proper place but shown why it
had
to occupy that place.
It was perfect, it was elegant, and it was wrong. As Kepler took more time to compare the actual sizes of the planets' orbits with the sizes his model predicted, he found mismatches he couldn't explain away. He tried endless fixes. Nothing. How could God have led him astray?
At last the light dawned. Kepler had been thinking in two dimensions, in the flat world of circles and triangles and squares. But the universe has three dimensions. How much time had he wasted? “And now I pressed forward again. Why look for two-dimensional forms to fit orbits in space? One has to look for three-dimensional formsâand, behold dear reader, now you have my discovery in your hands!”
The switch to three dimensions represented far more than a chance to salvage a pet theory. One of the riddles that tormented Kepler had to do with the number of planetsâthere were exactly six. (Uranus, Neptune, and Pluto were not yet known.
33
) Why had God picked six, Kepler asked, “instead of twenty or one hundred”? He had no idea, and all his fussing with squares and pentagons and hexagons had brought him no nearer to an answer.
But now he realized that he had overlooked a glaring clue. Euclid had proved, two thousand years before, that in three dimensions the story of symmetrical shapes has an extraordinary
twist. Working in two dimensions, you can draw an endless succession of perfectly symmetrical, many-sided figuresâ
triangles, squares, pentagons, hexagons, and so on, forever. If you had enough patience, you could draw a hundred-sided polygon or a thousand-sided one. (All you'd have to do is draw a circle, mark equally spaced dots on it, and then connect each one to its next-door neighbors.)
In three dimensions, where there is more room, you might expect the same storyâa handful of simple shapes like pyramids and cubes and then a cascade of increasingly complicated
ones. Just as a pyramid is made of triangles pasted together, and a
cube is made of squares, so you might guess that you could glue
fifty-sided shapes together, or thousand-sided ones, and make
infinitely many new objects.
But you can't. Euclid proved that there are exactly five “Pla
tonic solidsӉthree-dimensional objects where each face is
symmetrical and all the faces are identical. (If you needed dice to play a game, the mathematician Marcus du Sautoy points out, these five shapes are the only possible ones.) Here is the complete array. There are no others:
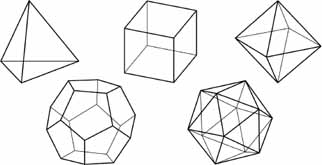
Only five. And there are six planets.
Now
Kepler had it. He still had to work out the details, but at last he'd seen the big picture. Each planet traveled around the sun, its orbit confined to a particular sphere. The spheres sat one inside the other. But what determined the sizes of the spheres? God, the greatest of all geometers, surely had a plan. After a false start, Kepler had seen it. Each sphere fit snugly and symmetrically inside a Platonic solid. Each Platonic solid, in turn, fit snugly and symmetrically inside a larger sphere. In a flash, Kepler saw why God had designed the cosmos to have six planets and why those orbits have the sizes they do. He burst into tears of joy.
“Now I no longer regretted the lost time,” he cried. “I no longer tired of my work; I shied from no computation, however difficult.” On and on he calculated, computing orbits, contemplating octahedrons and dodecahedrons, working without rest in the hope that at last he had it right but always terrified that once again his “joy would be carried away by the winds.”
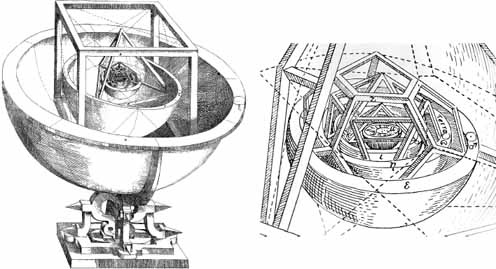
Kepler devised a new, more elaborate scheme to explain the planets' orbits. God had built the solar system around the five “Platonic solids.” The diagram at right, with the sun at its center, is a detail of the drawing at left. The sun sits inside a nested cage; the inmost shape is an octahedron.
But it wasn't. “Within a few days everything fell into its place. I saw one symmetrical solid after the other fit in so precisely between the appropriate orbits, that if a peasant were to ask you on what kind of hook the heavens are fastened so that they don't fall down, it will be easy for you to answer him.”
* * *
Kepler rejoiced in his success. “For a long time I wanted to become a theologian,” he told an old mentor. “For a long time I was restless. Now, however, behold how through my effort God is being celebrated through astronomy.”
In 1596 he presented his theory to the world in a book called
The Mystery of the Universe
. Even with his book completed, Kepler fretted about whether his model fit the actual data about
the planets' orbits quite well enough. For the time being, he managed to fight down his doubts. He happily devoted long hours to
constructing models of his solar system from colored paper and drawing plans for a version made of silver and adorned with diamonds and pearls. “No one,” he boasted, “ever produced a first work more deserving of admiration, more auspicious and, as far as its subject is concerned, more worthy.”
In the decades to come Kepler would make colossal discoveries, but his pride in his elaborate geometric model never faded. Centuries later the biologist James Watson would proclaim his double helix model of DNA “too pretty not to be true.” Kepler had felt the same joy and the same certainty, but eventually the data left him no choice but to acknowledge that he had gone wrong, again.
His perfect theory was only a fantasy, but it proved enormously fruitful even so. For one thing,
Mystery of the Universe
transformed Kepler's career. He sent a copy of the book to Tycho Brahe, the leading astronomer of the day, who found it impressive. In time Kepler would gain access to Tycho's immense and meticulous trove of astronomical data. He would pore over those figures incessantly, over the course of decades, trying to make his model work and uncovering other patterns concealed in the night sky. Later scientists would rummage through Kepler's collection of numerical discoveries and find genuine treasure among the dross.
Kepler valued
Mystery of the Universe
so highly because it was there that he had unveiled his great breakthrough. But in the
course of discussing his model of the heavens, he had scored
another history-making coup. Kepler had followed Copernicus
in placing the sun at the center of his model, but then Kepler
had moved a crucial step beyond all his predecessors. Not only did all the planets circle the sun, he noted, but the farther a planet was from the sun, the slower it traveled in its orbit. Somehow the sun must
propel
the planets, and whatever force it employed plainly grew weaker with distance.
Kepler had not yet found the law that described that forceâthat would take him another seventeen grueling yearsâbut this was a breakthrough even so. Astrologers and astronomers had always focused their attention on mapping the stars and charting the planets' journeys across the sky. The goal had been description and prediction, not explanation. No one before Kepler had ever focused on asking what it was that moved the planets on their way. From now on, scientists looking at the heavens would picture the stars and planets as actual, physical objects pushed and tugged by some cosmic engine and not simply as dots on a chart.
“Never in history,” marvels the historian of science Owen Gingerich, “has a book so wrong been so seminal in directing the future course of science.”
From the start Kepler's faith that God was a mathematician both impeded him and spurred him. First his faith lured him into devoting years to his Platonic pipe dream; when that dream dissolved it motivated him to search elsewhere, in the certain knowledge that there had to be
some
mathematical pattern that explained the solar system. Through all his years of searching, Kepler's fascination was less with the objects in the skyâthe sun, stars, and planetsâthan with the relationships among them. Not the things but the patterns. “Would that God deliver me from astronomy,” Kepler once wrote, “so I can devote all my time to my work on harmonies.”
In time that work would yield many patterns, a few of them among the highest achievements of human thought but most of them nearly inexplicable to modern readers. When Kepler finally abandoned his elaborate geometric model of the planets, for instance, he replaced it with an equally arcane model based
on music. This new search for “harmonies” built on Pythagoras's
age-old insight about strings of different lengths producing
notes of different pitch. Kepler's notion was that the planets in their various orbits, traveling at different speeds, corresponded to different musical notes, and “the heavenly motions are nothing but a continuous song for several voices (perceived by the intellect, not by the ear).
”
34
Kepler's new system, with its sopranos and tenors and basses, was as farfetched as its predecessor, with its cubes and pyramids and dodecahedrons. As it turned out, neither model had anything to do with reality. But in the course of his obsessive, misguided quest to prove the truth of his theories, Kepler did make genuine, epochal discoveries. Scientists would eventually dub three of these “Kepler's laws,” though Kepler never gave them that name nor deemed them any more praiseworthy than his other finds.
35
Late in his life, when he looked back over his career, Kepler himself could scarcely pick out his breakthroughs from the mathematical fantasies that surrounded them. “My brain gets tired when I try to understand what I wrote,” he said later, “and I find it hard to rediscover the connection between the figures and the text, that I established myself.”
Kepler was one of the most daring, insightful thinkers who ever lived, but his career only took off when he joined forces with an astronomer who was his opposite in almost every respect. Kepler was poor and lean, a creature of ribs and patches. Tycho Brahe was rich beyond measure. Kepler was shy and ascetic, Tycho hard-drinking and rowdy. Kepler was imaginative and creative, sometimes alarmingly so, Tycho a brilliant observer but a run-of-the-mill theoretician. But the two great astronomers needed one another.
Tycho
36
was a Danish nobleman with a private observatory on a private island. The most eminent astronomer of the generation before Kepler and Galileo, it was Tycho who had startled the world in 1572 by proving that the new star that had somehow materialized in the sky truly was a star. Nothing about Tycho was run-of-the-mill. Round, bald, sumptuously dressed, he looked like Humpty Dumpty with a walrus mustache and a velvet cloak. He ruled his mini-kingdom like a mini-king, presiding over lavish banquets and cackling over the antics of his court jester, a dwarf named Jepp.
In his student days, Tycho had lost part of his nose in a swordfight. In one version of the story, the trouble started at a wedding celebration when another wealthy young Dane reminded everyone of some odd events from a few months before. Tycho had announced with great fanfare, in a poem written in elegant Latin flourishes, that a recent eclipse of the moon foretold the death of the Turkish sultan. But, it turned out, the sultan had died six months
before
the eclipse. Tycho's rival told the story with gusto, and nearly all his listeners enjoyed it. Not Tycho. The retelling of the story led to bad blood and, soon after, a duel. Tycho nearly lost his life and did lose a chunk of his nose. For the rest of his life he sported a replacement made of gold and silver.
Despite the bluster and showmanship, Tycho was a genuine scholar. His observatory was the best in Europe, outfitted with a dazzling array of precision-made sextants, quadrants, and other devices for pinpointing the positions of stars. The observatory stood in a grand, turreted castle that boasted fourteen fireplaces and an astonishing luxury, running water. In Tycho's library stood a celestial globe five feet in diameter and made of brass; when a star's position was established beyond a doubt, a new dot was carefully added to the globe. Tycho boasted that his observatory had cost a ton of gold, and Kepler complained that “any single instrument cost more than my and my whole family's fortune put together.”
Kepler had sent his
Mystery of the Universe
to Tycho and all the other eminent scientists he could think of. Many could not fathom what he was up to. Tycho, more mystically minded than Galileo and some of the other skeptics, replied enthusiastically and soon took Kepler on as his assistant. It was an arrangement with obvious benefits for both men. Tycho had devised a hybrid model of the solar system, partway between the ancient Earth-centered model and Copernicus' sun-centered version. In this picture, the sun and moon orbited the Earth, and the five other planets orbited the sun. Tycho had compiled reams of scrupulously accurate observations, but without Kepler's mathematical help he could not demonstrate the truth of his hybrid model. Kepler had no interest in Tycho's model, but in order to make progress on his own theories he desperately needed Tycho's records.
But Tycho hoarded them. Torn between hope that the younger man could find patterns hidden within twenty years' worth of figures and fear that he was giving away his treasure, Tycho clung to his numbers with a miser's grip. Kepler snarled helplessly. And then, out of the blue, Tycho died. (He died of a bladder infection brought on, according to Kepler, by drinking too much at a banquet and refusing to leave the table to pee.) Kepler had been with Tycho only eighteen months, but now he had what he needed. “I was in possession of the observations,”
Kepler noted contentedly, “and refused to hand them over to
the heirs.”
