The Clockwork Universe (19 page)
Read The Clockwork Universe Online
Authors: Edward Dolnick

Science was now poised to confront one of its great taboos. The study of objects in motion had tempted and intimidated thinkers since ancient times. With his work on ramps and his discovery of the law of falling objects, Galileo had mounted the first successful assault. With his insights into graphs and the curves traced by moving points, Descartes had devised the tools that would make an all-out attack possible. Only one giant obstacle still blocked the way.
How did it happen that the Greeks, whose intellectual daring has never been surpassed, shied away from applying mathemat
ics to objects moving through space? In part because, as we have seen, they deemed impermanence an unworthy subject for mathematics, which investigated eternal truths. But they were skittish, too. That uneasiness was largely due to one man, named Zeno, who lived in a middle-of-nowhere Greek colony in southern Italy sometime around 450
B.C.
Zeno figured in one of Plato's
Dialogues
(Plato called him “tall and fair to look upon”), but almost all the facts about his life have been lost to us. So has almost every scrap of his writing. The few snippets that have survived have tied philosophers in knots from his day to ours.
Zeno's arguments sound silly at first, almost childish, for he was one of those philosophers who spoke not in polysyllables and abstractions but in stories. Only four of those tales have survived. Each is a tiny, paradoxical fable, a Borges parable unstuck in time by two millennia.
One story starts with a man standing in a room. His goal is to walk to the far side. Could anything be simpler? But before he can cross the room, Zeno points out, the man must first reach the halfway point. That will take a small but definite amount of time. And then he must cross half the distance that remains. Which will take a certain amount of time. Then half the still-remaining distance, and so on, forever. “Forever” is the key. A trip across the room, then, must pass through an infinite number of stages, each of which takes some definite, more-than-zero amount of time. And that could only mean, Zeno concluded gleefully, that a trip across the room would necessarily take an infinite amount of time.
Zeno certainly didn't believe that a man in a room was doomed to die before he could reach a doorway on the other side. His challenge to his fellow philosophers was not to cross a room but to find a mistake in his reasoning. On the one hand, everyone knew how to walk from here to there. On the other hand, that seemed impossible. What was going on?
For two thousand years, no one came up with a satisfactory answer. Philosophers debated endlessly, for instance, whether it even made sense to talk of dividing time into ever tinier bitsâis time continuous, like a ribbon, or is it more like a series of beads on a string? Can time be divided up forever or does it come in irreducible units, like atoms?
The Greeks quit in frustration early on. They did note that each of Zeno's tales began as a commonplace story having to do with motion and ended up circling around the strange notion of infinity. The danger zone seemed clear enough. Motion meant infinity, and infinity meant paradox. Having failed to find Zeno's error, Greek mathematicians opted to do the prudent thing. They put up emergency cones and yellow police tape and made a point of staying well clear of anything that involved the analysis of moving objects. “By instilling into the minds of the Greek geometers a horror of the infinite,” the mathematician Tobias Dantzig observed, “Zeno's arguments had the effect of a partial paralysis of their creative imagination. The infinite was taboo, it had to be kept out, at any cost.”
That banishment lasted twenty centuries.
Occasionally, during the long hiatus, a particularly bold thinker tiptoed to the brink of infinity, glanced down, and then hurried away. Albert of Saxony, a logician who lived in the 1300s, was one of the most insightful of this small band. To demonstrate just how strange a concept infinity is, Albert proposed a thought experiment. Imagine an infinitely long wooden beam, one inch high and one inch deep. Now take a saw and cut the beam into identical one-inch cubes. Since the beam is infinitely long, you can cut an infinite number of cubes.
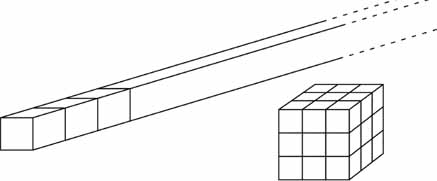
An infinitely long beam can be cut into blocks and then reassembled into bigger and bigger cubes.
What Albert did next was as surprising as a magic trick. The original beam, with a cross section of only one square inch, certainly did not take up much room. It went on forever, but you could easily hop over it. But if you took cubes from that beam and arranged them cleverly, Albert showed, you could fill the entire universe to the brim. The scheme was simple enough. All you had to do was build a small cube and then, over and over again, build a bigger cube around it.
First, you set a single cube on the ground. Then you made a 3 Ã 3 Ã 3 cube with the original cube at its center. That cube in turn became the center of a 5 Ã 5 Ã 5 cube, and so on. In time, the skinny beam that you began with would yield a series of colossal cubes that outgrew the room, the neighborhood, the solar system!
Once again, the moral was plain. To explore infinity was to tumble into paradox. Like the Greeks fifteen centuries before, medieval mathematicians edged away from the abyss.
Three hundred years later, Galileo ventured back toward forbidden territory. He began so innocuously that it seemed impos
sible he could fall into danger. Consider, Galileo said, one of
the humblest of all intellectual activities: matching, a skill even
more primitive than counting. How can we tell if two collections
are the same size? By taking one item from the first collection
and matching it with one from the other collection. Then we set those two aside and start over. How do we know that there are five
vowels? Because we can match them up with our five fingersâthe letter
a
with the thumb, say, and
e
with the index finger,
i
with the middle finger,
o
with the ring finger, and
u
with the pinky. Each vowel pairs off with a finger; each finger pairs off with a vowel; no member of either group is left over or left out.
Let us pause to make one more observation, which also seems utterly obvious. If we think of a groupâeveryone who lives in Italy, sayâand then we think of a smaller group contained within itâeveryone who lives in Romeâthen it seems beyond question that the original group is bigger than the subgroup.
In a moment, we will see why these points are worth belaboring. Suppose, said Galileo, we take not simply a big group, like the citizens of Italy, but an infinite group, like the counting numbers. Galileo wrote them in a line like this:
1 2 3 4 . . .
Next, said Galileo, suppose we think of a smaller group contained within the large one. Take, for instance, the numbers 1
2
, 2
2
, 3
2
, 4
2
, and so on. (In other words, the numbers 1, 4, 9, 16 . . . ). Galileo wrote them in a line of their own:
1
2
2
2
3
2
4
2
 . . .
Then he sprung his trap. Since the list 1, 4, 9, 16 . . . plainly leaves out a great many numbers, it is beyond question smaller than the collection of
all
numbers. But Galileo arranged the two lines of numbers one below the other and paired them up tidily.
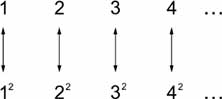
Each number in the top line had exactly one partner in the bottom line, and vice versa. Every number had a partner; no
number had more than one partner; and no number in either line
was left out. (The reason Galileo chose the numbers 1
2
, 2
2
, 3
2
 . . .
in the first place was that they could so readily be paired up with
1, 2, 3 . . .) That left only one conclusion. Since the two collections matched exactly, they were the same size. Galileo had
found a working definition of infinityâa collection is infinitely big if part of it is the same size as the whole thing!
Few thinkers in history have been as bold as Galileo, but even for him this was too much. For the sake of an idea, he would one day challenge the Inquisition. But faced with the paradoxes of infinity, he blinked and hurried away.
Galileo, brilliant in so many domains, had pinpointed infinity's strangest property. In a sense, big numbers are all alike. One million is bigger than one thousand, but you can get from one to the other. All it takes is patience. Add one. Add one more. Add another. Eventually you get there. But infinity sits on the far side of a chasm that you can never bridge. When it comes to infinity, it's not only that another (and another and another) doesn't bring you
to
the goal; worse than that, it doesn't bring you
any nearer
to the goal.
That idea, so remote from anything in the everyday world, continues to baffle even the deepest thinkers. In
Portrait of the Artist as a Young Man
, James Joyce took a stab at conveying the notion of infinity. The damned suffer eternally in hell. “For ever! For all eternity!” Joyce wrote. “Not for a year or for an age but for ever. Try to imagine the awful meaning of this. You have often seen the sand on the seashore. How fine are its tiny grains! And how many of those tiny little grains go to make up the small handful which a child grasps in its play. Now imagine a mountain of that sand, a million miles high, reaching from the earth to the farthest heavens, and a million miles broad, extending to remotest space, and a million miles in thickness. . . .”
On and on Joyce went, the limitlessly talented writer multiplying grains of sand by drops of water in the ocean by stars in the sky. And
still
he came up short, still he failed to narrow the gap between the finite and the infinite. Because the essential point is that infinity is not just a big number but something much, much more bizarre than that.

Isaac Newton was one of the greatest of all geniuses and one of the strangest men who ever lived. “The most fearful, cautious, and suspicious Temper that I ever knew,” in one contemporary's words, he was born sickly and premature but lived to 84 (and died a virgin). Born on Christmas Day, Newton believed with all his heart that he had been selected by God to decode His secrets. This portrait shows him at the peak of his powers, at age 46, just after he had unveiled the theory of gravitation.

Charles II, whose father had been beheaded in 1649, ruled England from 1660 to 1685. Witty and restless, the “Merrie Monarch” presided over a self-indulgent court in which everyone, from the king on down, was “engaged in an endless game of sexual musical chairs.” Science, too, fascinated Charles. He founded the Royal Society and poses here with a telescope and other scientific instruments.

Robert Boyle, an aristocrat whose father was one of Britain's richest men, was the most-respected member of the Royal Society in its early days. Boyle was a brilliant scientist who also believed, among other things, that the best cure for cataracts was to blow powdered, dried, human excrement into the patient's eyes.

Gottfried Leibniz was Newton's great rival and himself a man of astonishing genius. As energetic as a puppy, Leibniz was the temperamental opposite of the austere Newton. Leibniz was a philosopher, a mathematician, an inventor, and a man so pleased with himself that his favorite wedding gift to new brides was a collection of his own maxims.

The 1600s saw the birth of science and the modern age, but old beliefs and fears still held prominent places in men's hearts. Comets were dreaded, as they had been for ages. This scene from the Bayeux tapestry (stitched in the 11th century) shows men cowering in fear as Halley's Comet appears overhead, in 1066.
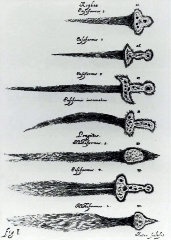
When our forebears looked at comets, they saw not merely glowing lights but fiery, death-wielding swords, as in these illustrations from 1668. Comets had appeared overhead in 1664 and 1665, and England braced for “a MORTALITY which will bring MANY to their Graves.”

In 1665, plague struck England. No one knew the cause, and no one knew a cure. Somehow the killer leaped from victim to victim. Many were healthy one day and dead that night. Plague doctors, shown here, could offer little but a kind word. Their costume was meant to protect the wearer; the beak contained herbs and spices, to counter the smell of the dead and dying.

Bills of Mortality recorded the weekly death toll. The first deaths in London came at a rate of one or two per month. At its peak, in September 1665, plague killed more than six thousand Londoners in a single week. The stricken city was nearly silent except for the tolling of church bells.

Samuel Pepys lived through the turmoil of London in the late 1600s and took notes in his diary, in a secret code. An administrator in the British navy, he reported on office politics, dalliances with mistresses, and fights with his wife. His accounts of the plague and the Great Fire of London are the most detailed descriptions we have.

As soon as the plague released England from its chokehold, a second calamity swooped down. In the year 1666âominous because of the fearsome number 666âLondon caught fire. For four days the city burned. Iron bars in prison cells melted. One hundred thousand people were left homeless. Plainly an outraged God had lost patience with his creation.

