The King of Infinite Space (10 page)
Read The King of Infinite Space Online
Authors: David Berlinski

The oil of compromise having been spread, the question, of course, remains. Which
does
comes first, geometry or arithmeticâfirst in the sense of being more fundamental, as bread is more fundamental than butter, and thus first in the sense that geometry may be derived from arithmetic, or arithmetic from geometry?
T
HE NATURAL NUMBERS
: 1, 2, 3, . . . Although the number 1 is smaller than all the rest, there is no number greater than any of the others. If there were such a number
n
, the number
n
+ 1 would be greater still. Does it follow that the natural numbers are infinite? The great Gauss offered a warning. “I protest,” Gauss remarks, “against the use of infinite magnitude as something completed, which is never permissible in mathematics. Infinity is merely a way of speaking.” The proper way to speak is to speak guardedly. The natural numbers are
potentially
infinite. The mathematician ascends from 1 to 2, from 2 to 3, and from
n
to
n
+ 1. But unless counting can go on
forever
, this analysis can hardly do justice to the natural numbers; and if it can go on forever,
why not admit the infinite once and for all and be done with it? Georg Cantor, the creator of set theory, argued in the late nineteenth century that the set of natural numbers comprises something infinite all at once, a great thing, complete in its luxuriance. What Cantor could not say is just how the human mind gains access to the infinite if not by climbing the staircase of the numbers, one step at a time. The natural numbers comprise an infinite set. Point to Cantor. Access to the infinite is incremental. Point to Gauss.
This is not Euclid's way.
I
N
B
OOKS
V, VII, and X of the
Elements
, Euclid talks about the numbers. “A unit,” he says, “is that by virtue of which each of the things that exist is called one.” A number is a “multitude composed of units.” Ancient commentators, writing before and after Euclid, suggested that a unit was the least or smallest answer to the question
how many?
The answer: just
one
. They were well aware, of course, that whatever
one
might be, it, too, could be divided, but this, they argued, would only return the mathematician to whatever multiplicities the number one was supposed to resolve in favor of the least of them.
Although Book VII of the
Elements
addresses the numbers explicitly, the book is logically subordinate to Book V. The numbers of Book VII are, in fact, the magnitudes of Book V. Book X of the
Elements
is in an act of double
deference subordinate to both. A rare lapse in organization is present throughout. Book V introduces Euclid's theory of magnitudes. It is widely considered one of Euclid's masterpieces, although whether by Euclid or whether a masterpiece are other questions. Historians of Greek mathematics now suggest that Euclid's theory is due largely to the Greek mathematician Eudoxus of Cnidus. Having anticipated the calculus with his method of exhaustion, Eudoxus also appears to have anticipated the real numbers with his theory of proportions. In his treatise
Elementary Geometry from an Advanced Standpoint
, the mathematician Edwin Moise argued that with respect to the real numbers, modern mathematicians had no need to create what Eudoxus had known all along.
With a unit fixedâa unit
chosen
âEuclid gains access to a geometrical simulacrum of the natural numbers and to the rational numbers or fractions, such as ½ or â
. The number 7 corresponds to 7 units laid tail to head, and the number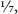 to the ratio of 1 unit to 7 of them.
to the ratio of 1 unit to 7 of them.
In the progression of the
Elements
, a magnitude represents a new idea, but the easy familiarity with which Euclid handles it suggests that he thought of magnitudes as natural aspects of his systemâfriends of the family. Euclid never quite says what a magnitude
is
, but the general idea is of extent, an occupation of space, an expanse. Whatever the expanse encompassed by a unit, it corresponds in the plane to
a straight line fixed between two points. This is how Euclid illustrates every one of his arithmetic ideas. It follows that the natural numbers, since they are without end, must correspond to the indefinite production of a straight line.
“It seems that the aging Plato,” René Thom remarked (with some indifference to the English language), “considered this type of generativity to be of the type [of] discrete generativity [that is characteristic] of the sequence of the natural integers.” The very old Plato may have murmured a word into the very young Euclid's ear; if not, his words were still within hearing distance.
A striking simile is at work in the
Elements
, one that is today anachronistic. Euclid had found the source of arithmetical generation in a geometrical object. The shadows play on the Euclidean plane. Beyond, there is the play of real things in the real world. Whence the simile. The Euclidean line moves in Euclidean space as a physical object moves in physical space. The idea occurred to many Greek mathematicians. It is the basis for the Greek scheme of geometrical algebra. As it works its way through Euclid's system, it introduces a degree of contrivance into Euclid's thoughts. The Euclidean line flows through the points that it touches, but it can be divided into discrete segments only by means of the geometer's retrospective artifice. From the outset, the Euclidean idea of number conflicts with the simile by which it is explained. In the end, what may seem
nothing more than a conceptual conflict grew until it threatened the integrity of the Euclidean system itself.
I
T IS NOT
disrespectfulâis it?âto say that geometrical algebra has in Euclid's hands all of the elegance of bears chained and taught to dance. In his proof of the Pythagorean theorem, Euclid ignores the algebraic equation in which the facts are so easily expressedâ
a
2
+
b
2
=
h
2
âand occupies himself with the construction of those rather oafish squares, seeing in their area the secret to the theorem's meaning. It is a clumsy business. The first proposition of Book II of the
Elements
affirms that the area of a given rectangle is equal to the sum of its subrectangles. This is in algebraic terms, the distributive law
a
(
b
+
c
+
d
) =
ab
+
ac
+
ad
, where
a
,
b
,
c
, and
d
are numbers. The rectangles are illustrations; they get in the way. Euclid takes geometrical algebra as far as he can go, but by the time he gets to where he is going, the tide must already have begun to turn. And while it took a long time to flow out, in the end it flew out, until mathematicians universally acknowledged the imperatives of analytic geometry, the countercurrent.
Writing in the seventeenth century, René Descartes created analytic geometry in a work titled
La Géométrie
. Descartes was not quite sure what he was doing. His great work he left almost as an afterthought. In analytic geometry, the Euclidean plane is made accessible, and so it is opened up,
by means of a coordinate system. A point is chosen arbitrarily, the origin. Since all points are in the end the same, it hardly matters
which
point is chosen. Whatever the point, it corresponds to the number zero. Thereafter, the point is bisected by two straight and perpendicular lines, the coordinate axes of the system. The positive natural numbers run from the origin out to infinity, the negative numbers run out the other way, back-street boys to the end, and precisely the same scheme is repeated for the vertical axis, making four line segments starting at zero and proceeding inexorably to the edge of the blackboard and the space beyond.
Any point in the plane may now be identified by a pair of numbers (
Figure VIII.1
). Hidden previously in the sameness of space, a point acquires a vivid arithmetical identity. It is
the
point corresponding to two numbers, where before it was some drab or other, anonymous. Once points have acquired their numerical identity, the mathematician can deploy the magnificent machinery of algebraic analysis to endow Euclidean geometry with a second and incomparably more vivid form of life.
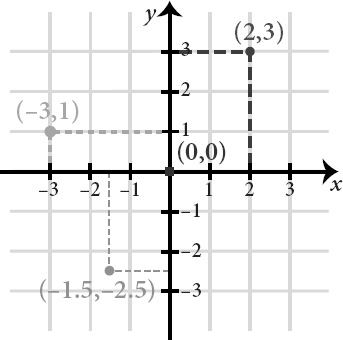
F
IGURE
VIII.1.
Euclidean coordinate system
A
RITHMETIC IS THE
place where the numbers are found, and algebra, the place where they are treated in their most general aspects. The points and straight lines of Euclidean geometryâmake of them what you will. They are undefined. Now that a geometrical point has been identified with a pair of numbers, a straight line can be defined by the equation
Ax
+
By
+
C
= 0, where
A
,
B
, and
C
are numerical parameters, fixed place markers, and
x
and
y
variables denoting points resident on the line.
Did Euclid have circles to command? He did. A circle whose center is at the point (
a
,
b
), and whose radius is
R
, is perfectly and completely described by the formula (
xâa
)
2
+ (
yâb
)
2
=
R
2
. The identity of the circle has been dominated by a numerical regime: its center is a pair of numbers; its radius, another number, and its circumference, an endless succession of numbers.
Analytic geometry has the power to depict a great many familiar geometrical shapes, such as the parabola, the ellipse,
and the hyperbola. There is also the
cardioid
, its penciled heart emerging from the billet-doux of (
x
2
+
y
2
+
ax
)
2
=
a
2
(
x
2
+ y
2
) (
Figure VIII.2
).
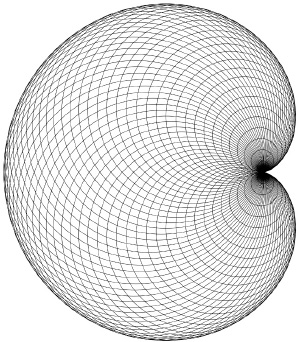
F
IGURE
VIII.2.
The cardioid
There are curves that look like a woman's smile, or the valley between hills, or the exuberant petals of some tropical flower.
There is an abundance.
I
N A LITTLE
book titled
The Coordinate Method
, a troika of Russian mathematicians (I. M. Gelfand, E. G. Glagoleva, and A. A. Kirillov) offers this account of analytic geometry: “By introducing coordinates, we establish a correspondence
between numbers and points of a straight line.” They then add: “In doing so, we exploit the following remarkable
fact
: There is a unique number corresponding to each point of the line and a unique point of the line corresponding to each number” (emphasis added). The remarkable fact to which they appeal is often described as the Cantor-Dedekind axiom, although how a fact could be an axiom, they do not say.
It hardly matters. There is no such fact, and neither is there any such axiom. There are some numbers that no accessible magnitude can express. In Book X of the
Elements
, Euclid offers a proof that this is so, one based on an earlier proof attributed to the Pythagorean school. He fails only to notice that what he has done constitutes an act of immolation.
