The King of Infinite Space (13 page)

Omar Khayyám, the author of the
Rubiyat
and a mathematician of distinction, made no effort to prove the parallel postulate. He was among the mathematical swappers. And he found nothing of interest:

T
URNING HIS HAND
to geometry after the rigors of his Jesuitical education, the seventeenth-century Italian mathematician Girolomo Saccheri published a treatise in 1733 optimistically titled
Euclides ab omni naevo vindicatus
(Euclid vindicated of every flaw). Very properly, he dismissed efforts to derive Euclid's parallel postulate directly from Euclid's other axioms. His Jesuit education allowed him to recognize that a dead end was dead. He turned the other way, assuming the parallel postulate false in order to derive that long fabled, fatal contradiction from his assumption. Saccheri was able to demonstrate many interesting propositions. He came very close to discovering non-Euclidean geometry; his Italian admirers, such as Beltrami, gave him as much credit for failing as they would have given a French mathematician for succeeding. Saccheri was shrewd, able, and penetrating. The contradiction that he anticipated, he never found.

It did not occur to him that it was not there. It did not occur to
anyone
.

There things stood until Gauss began to wonder, in the last years of the eighteenth century, whether the very attempt to derive Euclid's parallel postulate from Euclid's other axioms, or from anything at all, might not have been doomed, not simply difficult. No derivation had been achieved, Gauss reasoned, because none was possible. He was yet an adolescent, a young man of sixteen or seventeen. Remarkable ideas came to him often. Gauss declined to publish his thoughts later in his life, preferring, when others had published theirs, to remark that he had known it all along.

And often he had.

I
T IS POSSIBLE
, of course, to place Euclid's parallel postulate in protective custody, the little lunatic locked in a padded cell, so that the theorems that result are derived entirely from the first four of Euclid's assumptions. The system is called neutral geometry. It is hardly a description engendering excitement. Still, Euclid had demonstrated his first twenty-eight propositions by means of the axioms of neutral geometry; if nothing else, neutral geometry does the obvious. But it is the parallel postulate that is all mad glitter and glow and it does the rest.

The nineteenth-century mathematicians who had come to suspect the parallel postulate could choose whether to embrace it as an axiom or discard it as an impediment. Euclid had embraced his own. Bolyai and Lobachevsky rejected
what Euclid had embraced, arguing for an unembarrassed denial of the parallel postulate. The possibilities that emerged were unsettling. Over the course of two thousand years, Euclid's
Elements
had come to seem irrefragable. It had loomed as a monument. Now the monument seemed defaced, or if not defaced, then in some way damaged.

In the world beyond mathematics, non-Euclidean geometry represented a revolution in thought, and nineteenth-century thought was sympathetic to revolutions. It reveled in them. The details of non-Euclidean geometry were of interest only to mathematicians, of course, but its very existence provoked a certain anxiety among philosophers. “In addition to Euclidean geometry,” Bertrand Russell remarked in recalling his own experiences, “there were various non- Euclidean varieties, and . . . no one knew which was right.” A crack had opened in the crust of mathematics. Russell thought he saw something dreadful underneath. “If mathematics was doubtful, how much more doubtful ethics must be,” he wrote. “If nothing was known, it could not be known how a virtuous life should be lived.”

It is not surprising that Russell should recall that such inferences troubled his adolescence. Euclidean geometry had offered him a fixed point of certainty. Now it was gone. He felt adrift. All around him, similar inferences had gathered force. They are by no means anachronistic: they have retained their force. The impression is today widespread
that if it requires anything at all, science requires an unsentimental rejection of common sense, a recusal of principles that for thousands of years have served the human race. “My own suspicion,” the evolutionary biologist J. B. S. Haldane once remarked, “is that the Universe is not only queerer than we suppose, but queerer than we can suppose.”

What is either common sense or common human experience when set against such exorbitant queerness?

Mathematicians had for centuries struggled to prove Euclid's parallel postulate. They were right to sense its importance. They were wrong in thinking that they could prove it. In the nineteenth century, they gave up trying. The advent of non-Euclidean geometry signaled the first in a series of percussive shocks. If the new geometries were strange, theories to come would be stranger still. The claims of common sense and common experience were assessed and then rejected:

“Thou art weighed in the balances and thou art found wanting.”

O
DDLY ENOUGH
,
THE
possibilities for the development of non-Euclidean geometries should have been evident well before the nineteenth century. The captains of English, Spanish, and Portuguese ships crossing the great oceans knew perfectly well that a straight line was not necessarily the shortest distance between two points. It might have been
a clue, one that is obvious today from airplane flight. On the surface of the earth, the shortest distance between two points is the arc of a great curve. Flying from sunshine to sunshine, North American passengers often find themselves staring at the snows of some hyperborean horror in between one beach and another. Geometers call the arc of flight a
geodesic
, a useful term that has come to mean the shortest distance between any two points, no matter the underlying space.

The Euclidean plane is a surface of old, and so is the earth's surface, the first familiar from textbooks, the second from life. A spherical surface envelops a sphere, two dimensions wrapped around three. When the sphere is sliced by a plane passing through its center, the plane traces a circle on its interior surface. Between any two points, the circle describes a geodesic.

The surface of the earth is a model of spherical geometry. The Euclidean blackboard is flat, but the surface of the earth is curved—and curved in the same way at every point. It is
positively
curved, a designation that unaccountably suggests a geometrical accomplishment on the order of overeating. In spherical geometry, straight lines are arcs and there are no parallel lines at all. Wandering geodesics intersect one another as they circumnavigate the globe. Lines of latitude
are
parallel, but save for the equator, they are not geodesics. The interior angles of a triangle add up to more than 180 degrees. Euclidean figures bulge as if bursting.

If Euclid is demoted on the surface of a sphere, he cannot be altogether denied. Geodesics on the surface of a sphere rest, after all, on its
surface
. The interior of a sphere remains a part of the general Euclidean background. This veil of indifference dropped, Euclidean straight lines return to prominence. The shortest distance between two sunny beaches is a straight line drilled through the earth from point to point.

The drill is a reminder. Having been cast away, Euclid has a tendency to return to any exercise in non-Euclidean geometry as an enveloping space, a contrasting structure, an astonishingly durable ghost. That ghost—is he lingering for any good reason? An ant may determine the non-Euclidean character of a sphere without
any
Euclidean contrast at her disposal. She may well conclude from purely local clues that the surface of a sphere is curved.

Clever ant.

But while the ant is looking at the surface of the sphere, who is looking at the ant, and from which perspective?

Enter ghost.

G
AUSS HAD GRASPED
the principles of non-Euclidean geometry; he had entertained his provocative thoughts in the silence of his study. It was left to the Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Ivanovich Lobachevsky to do the rest.

No story in the history of mathematics is more romantic. Bolyai's father, Farkas, had been an amateur mathematician; he was often in correspondence with Gauss. Euclid's parallel postulate obsessed him. Failure to establish the parallel postulate he regarded as “an eternal cloud on virgin truth.” The proofs that he sent eagerly to Gauss, Gauss promptly returned, the errors marked. Bolyai's son, János, was a prodigy and a polyglot, the master of nine difficult languages, a mathematician of distinction, a man of many gifts. High- strung and independent, he was consumed by duels, dances, and debts; he spent years in military service. And like his father, he was obsessed by the parallel postulate.

His father saw his son advancing toward the sinister, dark defile that had for so long obsessed him. He endeavored to warn him by means of letters that mingled the plan-gency and hysteria of a train's whistle: “Do not in any case have anything to do with the parallels. I know every twist and turn in this business and I have myself wandered in its fathomless night, which has extinguished every light and joy in my life. I beg you in the name of God. Leave the parallels in peace.”
²

There is the rattle of thunder in all the old Hungarian clouds, a flash of lightening, claptraps accumulating, father and son receding:

M
UCH FURTHER TO
the east, a Russian mathematician, Nikolai Ivanovitch Lobachevsky, was entering the same dark defile and finding it altogether to his taste. Like Bolyai, Lobachevsky was a man of intellectual powers that had been celebrated from his youth. He was original, determined, disciplined, and hardworking. When officials at the University of Kazan discovered that he was prepared to do well any task assigned him, they assigned him every task and quickly took it for granted that he would do them well. They were not mistaken. Knowing little about architecture, Lobachevsky designed a stately and imposing university building. He became the administrative center of mathematical life, reading scholarship applications, searching out other mathematicians,
placating and pleasing the faculty, and skillfully managing the bureaucracy by which the university lived, its endless accountants, survey takers, patronage peddlers, censors. He took charge of the university library. Until his tenure, it had been little used and poorly managed, the mice scampering through its shelves. He bound the old books and ordered new journals; he cleaned the place up.

L
OBACHEVSKY
'
S REJECTION OF
the parallel postulate, which he published in
The Kazan Messenger
in 1829, could not have been more severe. Instead of the Euclidean plane of old, there is the hyperbolic plane of new. Both planes are planes in that they are two-dimensional surfaces. There the similarity ends. Were the hyperbolic plane like the Euclidean plane, there would be no point in denying Euclid's parallel postulate. In that way, lies madness.

Lobachevsky's illustrations of the hyperbolic plane were contrived to fit into a small region of the Euclidean plane, but beyond the margins of the illustrations, the hyperbolic plane departs from flatness, turning itself over like an inside-out orange peel. The illustrations nonetheless convey what is unusual and strange. There is a straight line R, a point
B
marked on the line, a point
P
lying beyond R; there are straight lines
x
and
y
that pass through
P
; and there is an angle θ (
Figure IX.1
).

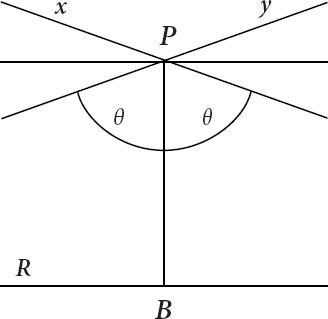
F
IGURE
IX.1.
The hyperbolic plane

If θ is less than ninety degrees, straight lines passing through
P
will sooner or later intersect line R. If θ equals 90 degrees, a reversion to Euclid. The reversion marks the limits of the familiar.

But if θ is
greater
than 90 degrees? First, those straight lines are straight. Second, they are parallel to line R. And, third, there is
more than one
of them.

The theorems that follow are an imposition on common sense. The interior angles of a hyperbolic triangle sum to
less
than 180 degrees: A + B + C < π. Similar triangles are congruent. Lines that are parallel to a given line need not be parallel to one another. The circumference of a circle whose radius is R is
greater
than 2πR.