Thinking, Fast and Slow (50 page)
Read Thinking, Fast and Slow Online
Authors: Daniel Kahneman

Imaginability plays an important role in the evaluation of probabilities in real-life situations. The risk involved in an adventurous expedition, for example, is evaluated by imagining contingencies with which the expedition is not equipped to cope. If many such difficulties are vividly portrayed, the expedition can be made to appear exceedingly dangerous, although th
e ease with which disasters are imagined need not reflect their actual likelihood. Conversely, the risk involved in an undertaking may be grossly underestimated if some possible dangers are either difficult to conceive of, or simply do not come to mind.
Illusory correlation
. Chapman and Chapman
17
have described an interesting bias in the judgment of the frequency with which two events co-occur. They presented naive judges with information concerning several hypothetical mental patients. The data for each patient consisted of a clinical diagnosis and a drawing of a person made by the patient. Later the judges estimated the frequency with which each diagnosis (such as paranoia or suspiciousness) had been accompanied by various features of the drawing (such as peculiar eyes). The subjects markedly overestimated the frequency of [ frpici co-occurrence of natural associates, such as suspiciousness and peculiar eyes. This effect was labeled illusory correlation. In their erroneous judgments of the data to which they had been exposed, naive subjects “rediscovered” much of the common, but unfounded, clinical lore concerning the interpretation of the draw-a-person test. The illusory correlation effect was extremely resistant to contradictory data. It persisted even when the correlation between symptom and diagnosis was actually negative, and it prevented the judges from detecting relationships that were in fact present.
Availability provides a natural account for the illusory-correlation effect. The judgment of how frequently two events co-occur could be based on the strength of the associative bond between them. When the association is strong, one is likely to conclude that the events have been frequently paired. Consequently, strong associates will be judged to have occurred together frequently. According to this view, the illusory correlation between suspiciousness and peculiar drawing of the eyes, for example, is due to the fact that suspiciousness is more readily associated with the eyes than with any other part of the body.
Lifelong experience has taught us that, in general, instances of large classes are recalled better and faster than instances of less frequent classes; that likely occurrences are easier to imagine than unlikely ones; and that the associative connections between events are strengthened when the events frequently co-occur. As a result, man has at his disposal a procedure (the availability heuristic) for estimating the numerosity of a class, the likelihood of an event, or the frequency of co-occurrences, by the ease with which the relevant mental operations of retrieval, construction, or association can be performed. However, as the preceding examples have demonstrated, this valuable e
stimation procedure results in systematic errors.
Adjustment and Anchoring
In many situations, people make estimates by starting from an initial value that is adjusted to yield the final answer. The initial value, or starting point, may be suggested by the formulation of the problem, or it may be the result of a partial computation. In either case, adjustments are typically insufficient.
18
That is, different starting points yield different estimates, which are biased toward the initial values. We call this phenomenon anchoring.
Insufficient adjustment
. In a demonstration of the anchoring effect, subjects were asked to estimate various quantities, stated in percentages (for example, the percentage of African countries in the United Nations). For each quantity, a number between 0 and 100 was determined by spinning a wheel of fortune in the subjects’ presence. The subjects
were instructed to indicate first whether that number was higher or lower than the value of the quantity, and then to estimate the value of the quantity by moving upward or downward from the given number. Different groups were given different numbers for each quantity, and these arbitrary numbers had a marked effect on estimates. For example, the median estimates of the percentage of African countries in the United Nations were 25 and 45 for groups that received 10 and 65, respectively, as starting points. Payoffs for accuracy did not reduce the anchoring effect.
Anchoring occurs not only when the starting point is given to the subject, but also when the subject bases his estimate on the result of some incomplete computation. A study of intuitive numerical estimation illustrates this effect. Two groups of high school student [choult os estimated, within 5 seconds, a numerical expression that was written on the blackboard. One group estimated the product
8 ×7 ×6 ×5 ×4 ×3 ×2 ×1
while another group estimated the product
1 ×2 ×3 ×4 ×5 ×6 ×7 ×8
To rapidly answer such questions, people may perform a few steps of computation and estimate the product by extrapolation or adjustment. Because adjustments are typically insufficient, this procedure should lead to underestimation. Furthermore, because the result of the first few steps of multiplication (performed from left to right) is higher in the descending sequence than in the ascending sequence, the former expression should be judged larger than the latter. Both predictions were confirmed. The median estimate for the ascending sequence was 512, while the median estimate for the descending sequence was 2,250. The correct answer is 40,320.
Biases in the evaluation of conjunctive and disjunctive events
. In a recent study by Bar-Hillel
19
subjects were given the opportunity to bet on one of two events. Three types of events were used: (i) simple events, such as drawing a red marble from a bag containing 50% red marbles and 50% white marbles; (ii) conjunctive events, such as drawing a red marble seven times in succession, with replacement, from a bag containing 90% red marbles and 10% white marbles; and (iii) disjunctive events, such as drawing a red marble at least once in seven successive tries, with replacement, from a bag containing 10% red marbles and 9% white marbles. In this problem, a significant majority of subjects preferred to bet on the conjunctive event (the probability of which is .48) rather than on the simple event (the probability of which is .50). Subjects also preferred to bet on the simple event rather than on the disjunctive event, which has a probability of .52. Thus, most subjects bet on the less likely event in both comparisons. This pattern of choices illustrates a general finding. Studies of choice among gambles and of judgments of probability indicate that people tend to overestimate the probability of conjunctive events
20
and to underestimate the probability of disjunctive events. These biases are readily explained as effects of anchoring. The stated probability of the elementary event (success at any one stage) provides a natural starting point for the estimation of the probabilities of both conjunctive and disjunctive events. Since adjustment from the starting point is typically insufficient, the final estimates remain too close to the probabilities of the elementary events in both cases. Note that the overall probability of a conjunctive event is lower than the probability of each elementary event, whereas the overall probability of a disjunctive event is h
igher than the probability of each elementary event. As a consequence of anchoring, the overall probability will be overestimated in conjunctive problems and underestimated in disjunctive problems.
Biases in the evaluation of compound events are particularly significant in the context of planning. The successful completion of an undertaking, such as the development of a new product, typically has a conjunctive character: for the undertaking to succeed, each of a series of events must occur. Even when each of these events is very likely, the overall probability of success can be quite low if the number of events is large. The general tendency to overestimate the pr [timrall obability of conjunctive events leads to unwarranted optimism in the evaluation of the likelihood that a plan will succeed or that a project will be completed on time. Conversely, disjunctive structures are typically encountered in the evaluation of risks. A complex system, such as a nuclear reactor or a human body, will malfunction if any of its essential components fails. Even when the likelihood of failure in each component is slight, the probability of an overall failure can be high if many components are involved. Because of anchoring, people will tend to underestimate the probabilities of failure in complex systems. Thus, the direction of the anchoring bias can sometimes be inferred from the structure of the event. The chain-like structure of conjunctions leads to overestimation, the funnel-like structure of disjunctions leads to underestimation.
Anchoring in the assessment of subjective probability distributions
. In decision analysis, experts are often required to express their beliefs about a quantity, such as the value of the Dow Jones average on a particular day, in the form of a probability distribution. Such a distribution is usually constructed by asking the person to select values of the quantity that correspond to specified percentiles of his subjective probability distribution. For example, the judge may be asked to select a number,
X
90
, such that his subjective probability that this number will be higher than the value of the Dow Jones average is .90. That is, he should select the value
X
90
so that he is just willing to accept 9 to 1 odds that the Dow Jones average will not exceed it. A subjective probability distribution for the value of the Dow Jones average can be constructed from several such judgments corresponding to different percentiles.
By collecting subjective probability distributions for many different quantities, it is possible to test the judge for proper calibration. A judge is properly (or externally) calibrated in a set of problems if exactly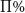 % of the true values of the assessed quantities falls below his stated values of
% of the true values of the assessed quantities falls below his stated values of
X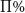 . For example, the true values should fall below
. For example, the true values should fall below
X
01
for 1% of the quantities and above
X
99
for 1% of the quantities. Thus, the true values should fall in the confidence interval between
X
01
and
X
99
on 98% of the problems.
Several investigators
21
have obtained probability distributions for many quantities from a large number of judges. These distributions indicated large and systematic departures from proper calibration. In most studies, the actual values of the assessed quantities are either smaller than
X
0l
or greater than
X
99
for about 30% of the problems. That is, the subjects state overly narrow confidence intervals which reflect more certainty than is justified by their knowledge about the assessed quantities. This bias is common to naive and to sophisticated subjects, and it is not eliminated by introducing proper scoring rules, which provide incentives for external calibration. This effect is attributable, in part at least, to anchoring.
To select
X
90
for the value of the Dow Jones average, for example, it is natural to begin by thinking about one’s best estimate of the Dow Jones and to adjust this value upward. If this adjustment—like most others—is insufficient, then
X
90
will not be sufficiently extreme. A similar a
nchoring [lariciently effect will occur in the selection of
X
10
, which is presumably obtained by adjusting one’s best estimate downward. Consequently, the confidence interval between
X
10
and
X
90
will be too narrow, and the assessed probability distribution will be too tight. In support of this interpretation it can be shown that subjective probabilities are systematically altered by a procedure in which one’s best
estimate does not serve as an anchor.
