Understanding Computation (18 page)

>>dfa_design=simulation.to_dfa_design=> #>>dfa_design.accepts?('aaa')=> false>>dfa_design.accepts?('aab')=> true>>dfa_design.accepts?('bbbabb')=> true
Excellent!
At the beginning of this section, we asked whether the extra features of NFAs let us do
anything that we can’t do with a DFA. It’s clear now that the answer is no, because if any NFA
can be turned into a DFA that does the same job, NFAs can’t possibly have any extra power.
Nondeterminism and free moves are just a convenient repackaging of what a DFA can already do,
like syntactic sugar in a programming language, rather than new capabilities that take us
beyond what’s possible within the constraints of determinism.
It’s theoretically interesting that adding more features to a simple machine didn’t make
it fundamentally any more capable, but it’s also useful in practice, because a DFA is easier
to simulate than an NFA: there’s only a single current state to keep track of, and a DFA is
simple enough to implement directly in hardware, or as machine code that uses program
locations as states and conditional branch instructions as rules. This means that a regular
expression implementation can convert a pattern into first an NFA and then a DFA, resulting in
a very simple machine that can be simulated quickly and
efficiently.
Some DFAs have the
property of being
minimal
, which means there’s no way to
design a DFA with fewer states that will accept the same strings. The NFA-to-DFA conversion
process can sometimes produce nonminimal DFAs that contain redundant states, but there’s an
elegant way to eliminate this redundancy, known
as
Brzozowski’s algorithm
:
Begin with your nonminimal DFA.
Reverse all of the rules. Visually, this means that every arrow in the machine’s
diagram stays in the same place but points backward; in code terms, everyFARule.new(state, character, next_state)is replaced withFARule.new(next_state, character, state). Reversing
the rules usually breaks the determinism constraints, so now you have an NFA.Exchange the roles of start and accept states: the start state
becomes an accept state, and each of the accept states becomes a
start state. (You can’t directly convert all the accept states into
start states because an NFA can only have one start state, but you
can get the same effect by creating a new start state and connecting
it to each of the old accept states with a free move.)Convert this reversed NFA to a DFA in the usual way.
Surprisingly, the resulting DFA is guaranteed to be minimal and contain no redundant
states. The unhappy downside is that it will only accept
reversed
versions of the original DFA’s strings: if our original DFA accepted the strings'ab','aab','aaab', and so on, the minimized DFA will accept strings of the
form'ba','baa', and'baaa'. The trick is to fix this by simply performing
the whole procedure a second time, beginning with the reversed DFA and ending up with a
double-reversed DFA, which is again guaranteed to be minimal but this time accepts the same
strings as the machine we started with.
It’s nice to have an automatic way of eliminating redundancy in a design, but
interestingly, a minimized DFA is also
canonical
: any two DFAs that
accept exactly the same strings will minimize to the same design, so we can check whether
two DFAs are equivalent by minimizing them and comparing the resulting machine designs to
see if they have the same structure.
[
28
]
This in turn gives us an elegant way of checking whether two regular expressions
are equivalent: if we convert two patterns that match the same strings (e.g.,ab(ab)*anda(ba)*b) into
NFAs, convert those NFAs into DFAs, then minimize both DFAs with Brzozowski’s algorithm,
we’ll end up with two identical-looking machines.
[
20
]
This design is general enough to accommodate different kinds
of machines and rules, so we’ll be able to reuse it later in the
book when things get more complicated.
[
21
]
A finite automaton has no record of its own history and no storage aside from its
current state, so two identical machines in the same state are interchangeable for any
purpose.
[
22
]
This NFA actually accepts any string ofacharacters except for the single-character string'a'.
[
23
]
Technically speaking, this process computes a
fixed point
of
the “add more states by following free moves” function.
[
24
]
In this simple case, we could get away with just turning the original start state
into an accept state instead of adding a new one, but in more complex cases (e.g.,(a*b)*), that technique can produce a machine that
accepts other undesirable strings in addition to the empty string.
[
25
]
RE2’s tagline is “an efficient, principled regular
expression library,” which is difficult to argue with.
[
26
]
Although an NFA only has one start state, free moves can make other states
possible before any input has been read.
[
27
]
The worst-case scenario for a simulation of a three-state NFA is “1,” “2,” “3,” “1 or
2,” “1 or 3,” “2 or 3,” “1, 2, or 3” and “none.”
[
28
]
Solving this
graph isomorphism problem
requires a clever
algorithm in itself, but informally, it’s easy enough to look at two machine diagrams
and decide whether they’re “the same.”
In
Chapter 3
, we investigated finite automata, imaginary machines that strip away the complexity of a
real computer and reduce it to its simplest possible form. We explored the behavior of those
machines in detail and saw what they’re useful for; we also discovered that, despite having an
exotic method of execution, nondeterministic finite automata have no more power than their more
conventional deterministic counterparts.
The fact that we
can’t make a finite automaton more capable by adding fancy features like
nondeterminism and free moves suggests that we’re stuck on a plateau, a level of computational
power that’s shared by all these simple machines, and that we can’t break away from that plateau
without making more drastic changes to the way the machines work. So how much power do all these
machines really have? Well, not much. They’re limited to a very specific application—accepting
or rejecting sequences of characters—and even within that small scope, it’s still easy to come
up with languages that no machine can recognize.
For example, think about designing a finite state machine capable of
reading a string of opening and closing brackets and accepting that string
only if the
brackets are
balanced
—that is, if each
closing bracket can be paired up with an opening bracket from earlier in the
string.
[
29
]
The general
strategy for solving this problem is to read characters one at a time while keeping
track of a number that represents the current
nesting level
: reading an
opening bracket increases the nesting level, and reading a closing bracket decreases it.
Whenever the nesting level is zero, we know that the brackets we’ve read so far are
balanced—because the nesting level has gone up and come down by exactly the same amount—and if
we try to decrease the nesting level below zero, then we know we’ve seen too many closing
brackets (e.g.,'())') and that the string must be
unbalanced, no matter what its remaining characters are.
We can make a
respectable start at designing an NFA for this job. Here’s one
with four states:
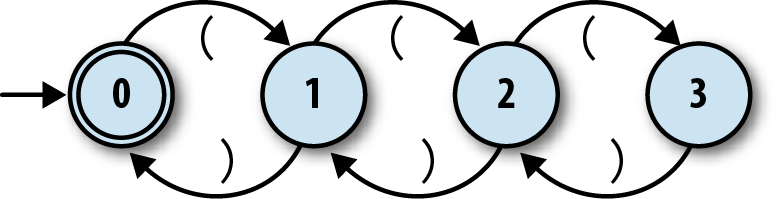
Each
state corresponds to a particular nesting level, and reading
an opening or closing bracket moves the machine into a state for a higher or
lower level respectively, with “no nesting” being the accept state. Since
we’ve already implemented everything we need to simulate this NFA in Ruby,
let’s fire it up:
>>rulebook=NFARulebook.new([FARule.new(0,'(',1),FARule.new(1,')',0),FARule.new(1,'(',2),FARule.new(2,')',1),FARule.new(2,'(',3),FARule.new(3,')',2)])=> #>>nfa_design=NFADesign.new(0,[0],rulebook)=> #
Our NFA design works fine on certain inputs. It can tell that'(()'and'())'aren’t balanced and that'(())'is, and it even has no problem spotting more
elaborate balanced strings like'(()(()()))':
>>nfa_design.accepts?('(()')=> false>>nfa_design.accepts?('())')=> false>>nfa_design.accepts?('(())')=> true>>nfa_design.accepts?('(()(()()))')=> true
But the design has a serious flaw: it’ll fail as soon as the brackets become nested more
than three levels deep. It doesn’t have enough states to keep track of the nesting in a string
like'(((())))', so it rejects that string even though the
brackets are clearly balanced:
>>nfa_design.accepts?('(((())))')=> false
We can fix this temporarily by adding more states. An NFA with five states can recognize'(((())))'and any other balanced string with fewer than
five levels of nesting, and an NFA with ten, a hundred, or a thousand states can recognize any
balanced string whose nesting level stays within that machine’s hard limit. But how can we
design an NFA that can recognize
any
balanced string, to an arbitrary level
of nesting? It turns out that we can’t: a finite automaton must always have a finite number of
states, so for any given machine, there’s always a finite limit to how many levels of nesting it
can support, and we can always break it by asking about a string whose brackets nest one level
deeper than it can handle.
The underlying problem is that a finite automaton has only limited storage in the form of
its fixed collection of states, which means it has no way to keep track of an
arbitrary
amount of information. In the case of the balanced brackets
problem, an NFA can easily count up to some maximum number baked into its design, but it can’t
keep counting indefinitely to accommodate inputs of any possible size.
[
30
]
This doesn’t matter for jobs that are inherently fixed in size, like matching the
literal string'abc', or ones where there’s no need to keep
track of the amount of repetition, like matching the regular expressionab*c, but it does make finite automata unable to handle tasks where an
unpredictable amount of information needs to be stored up during the computation and reused
later.
We’ve seen that
finite automata are intimately related to regular expressions.
Semantics
showed how to turn any regular expression into an
NFA, and in fact, there’s another algorithm for
converting any NFA back into a regular
expression again.
[
31
]
This tells us that regular expressions are equivalent to NFAs and have the same
limitations, so it can’t be possible to use a regular expression to recognize balanced strings
of brackets, or any other language whose definition involves pairs of things that nest to an
arbitrary depth.
Perhaps the best-known example of this weakness is the fact that
regular expressions can’t
distinguish between valid and invalid HTML
. Many HTML elements
require opening and closing tags to appear in pairs, and those pairs can
themselves enclose other elements, so finite automata don’t have enough
power to read a string of HTML while keeping track of which unclosed tags
have been seen and how deeply they’re nested.
In practice, though, real-world “regular expression” libraries often
go beyond what regular expressions are technically capable of. Ruby’sRegexpobjects have many features that
aren’t part of the formal definition of regular expressions, and those
bonus features provide enough extra power to allow more languages to be
recognized.
One ofRegexp’s enhancements is
the ability to label a subexpression with the(?<syntax and then “call” that subexpression elsewhere withname>)\g<. Beingname>
able to refer to its own subexpressions allows aRegexpto call itself recursively, which makes
it possible to match nested pairs to an arbitrary depth.
For example, subexpression calls let us write
aRegexpthat actually
does match balanced strings of brackets, even though NFAs (and therefore,
technically, regular expressions) can’t do it. Here’s what thatRegexplooks like:
balanced=/\A # match beginning of string(?# begin subexpression called "brackets" \( # match a literal opening bracket\g* # match "brackets" subexpression zero or more times \) # match a literal closing bracket) # end subexpression* # repeat the whole pattern zero or more times\z # match end of string/x
The(?subexpression matches a single
pair of opening and closing brackets, but inside that pair, it can match any number of
recursive occurrences of itself, so the whole pattern can correctly identify brackets nested
to any depth:
>>['(()','())','(())','(()(()()))','((((((((((()))))))))))'].grep(balanced)=> ["(())", "(()(()()))", "((((((((((()))))))))))"]
This only works because Ruby’s regular expression engine uses
a
call stack
to keep track of the recursive invocations of(?, something that DFAs and NFAs can’t
do. In the next section, we’ll see how to extend finite automata to give them exactly this
sort of power.
And yes, you could use the same idea to write aRegexpthat matches properly nested HTML tags,
but it’s guaranteed not to be a good use of your time.
It’s clear that there are limitations to these machines’ capabilities.
If nondeterminism isn’t enough to make a finite automaton more capable, what
else can we do to give it more power? The current problems stem from the
machines’ limited storage, so let’s add some extra storage and
see what
happens.
We can solve the storage
problem by extending a finite state machine with some
dedicated scratch space where data can be kept during computation. This
space gives the machine a sort of
external memory
in addition to the limited internal memory provided by its state—and as
we’ll discover, having an external memory makes all the difference to a
machine’s computational power.
A simple way to
add storage to a finite automaton is to give it access to a
stack
, a last-in first-out data structure that characters can be
pushed onto and then popped off again. A stack is a simple and restrictive data
structure—only the top character is accessible at any one time, we have to discard the top
character to find out what’s underneath it, and once we’ve pushed a sequence of characters
onto the stack, we can only pop them off in reverse order—but it does neatly deal with the
problem of limited storage. There’s no built-in limit to the size of a stack, so in
principle, it can grow to hold as much data as necessary.
[
32
]
A finite state machine with a built-in stack is
called a
pushdown automaton
(PDA), and when that
machine’s rules are deterministic, we call it a
deterministic pushdown automaton
(DPDA). Having access to a stack
opens up new possibilities; for example, it’s easy to design a DPDA that recognizes balanced
strings of brackets. Here’s how it works:
Give the machine two states, 1 and 2, with state 1 being the accept state.
Start the machine in state 1 with an empty stack.
When in state 1 and an opening bracket is read, push some character—let’s use
bfor “bracket”—onto the stack and move into state
2.When in state 2 and an opening bracket is read, push the character
bonto the stack.When in state 2 and a closing bracket is read, pop the character
boff the stack.When in state 2 and the stack is empty, move back into state 1.
This DPDA uses the size of the stack to count how many unclosed opening brackets it’s
seen so far. When the stack’s empty it means that every opening bracket has been closed, so
the string must be balanced. Watch how the stack grows and shrinks as the machine reads the
string'(()(()()))':
| State | Accepting? | Stack contents | Remaining input | Action |
| 1 | yes | | (()(()())) | read(, pushb, go to state 2 |
| 2 | no | b | ()(()())) | read(, pushb |
| 2 | no | bb | )(()())) | read), popb |
| 2 | no | b | (()())) | read(, pushb |
| 2 | no | bb | ()())) | read(, pushb |
| 2 | no | bbb | )())) | read), popb |
| 2 | no | bb | ())) | read(, pushb |
| 2 | no | bbb | ))) | read), popb |
| 2 | no | bb | )) | read), popb |
| 2 | no | b | ) | read), popb |
| 2 | no | | | go to state 1 |
| 1 | yes | | | — |
The idea behind
the balanced-brackets DPDA is straightforward, but there
are some fiddly technical details to work out before we can actually
build it. First of all, we have to decide exactly how pushdown automata
rules should work. There are several design issues here:
Does every rule have to modify the stack, or read input, or
change state, or all three?Should there be two different kinds of rule for pushing and
popping?Do we need a special kind of rule for changing state when the
stack is empty?Is it okay to change state without reading from the input,
like a free move in an NFA?If a DPDA can change state spontaneously like that, what does
“deterministic” mean?
We can answer all of these questions by choosing a single rule
style that is flexible enough to support everything we need. We’ll break
down a PDA rule into five parts:
The current state of the machine
The character that must be read from the input (optional)
The next state of the machine
The character that must be popped off the stack
The
sequence
of characters to push onto the stack after the top
character has been popped off
The first three parts are familiar from DFA and NFA rules. If a rule doesn’t want the
machine to change state, it can make the next state the same as the current one; if it
doesn’t want to read any input (i.e., a free move), it can omit the input character, as long
as that doesn’t make the machine nondeterministic (see
Determinism
).
The other two parts—a character to pop and a sequence of characters to push—are specific
to PDAs. The assumption is that a PDA will
always
pop the top character
off the stack, and then push some other characters onto the stack, every time it follows a
rule. Each rule declares which character it wants to pop, and the rule will only apply when
that character is on the top of the stack; if the rule wants that character to stay on the
stack instead of getting popped, it can include it in the sequence of characters that get
pushed back on afterward.
This five-part rule format doesn’t give us a way to write rules that apply when the
stack is empty, but we can work around that by choosing a special character to mark the
bottom of the stack—the dollar sign,$, is a popular
choice—and then checking for that character whenever we want to detect the empty stack. When
using this convention, it’s important that the stack never becomes truly empty, because no
rule can apply when there’s nothing on the top of the stack. The machine should start with
the special bottom symbol already on the stack, and any rule that pops that symbol must push
it back on again afterward.
It’s easy enough to rewrite the balanced-bracket DPDA’s rules in
this format:
When in state 1 and an opening bracket is read, pop the character
$, push the charactersb$, and move into state 2.When in state 2 and an opening bracket is read, pop the character
b, push the charactersbb, and stay in state 2.When in state 2 and a closing bracket is read, pop the character
b, push no characters, and stay in state 2.When in state 2 (without reading any character), pop the character
$, push the character$,
and move into state 1.
We can show these rules on a diagram of the machine. A DPDA
diagram looks a lot like an NFA diagram, except that each arrow needs to
be labelled with the characters that are popped and pushed by that rule
as well as the character that it reads from the input. If we use the
notationa;b/cdto label a rule that
readsafrom the input, popsbfrom the stack, and then pushescdonto the stack, the machine looks like
this:
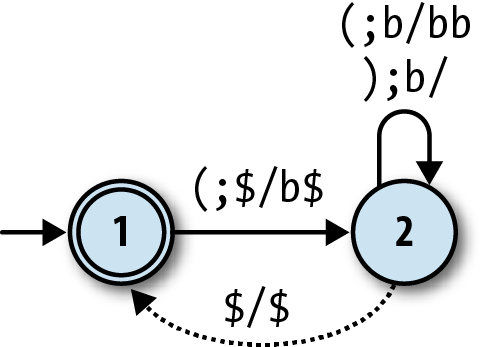
The next hurdle is
to define exactly what it means for a PDA to be deterministic. For DFAs, we had
the “no contradictions” constraint: there should be no states where the machine’s next move
is ambiguous because of conflicting rules. The same idea applies to DPDAs, so for example,
we can only have one rule that applies when the machine’s in state 2, the next input
character is an opening bracket, and there’s abon the
top of the stack. It’s even okay to write a free move rule that doesn’t read any input, as
long as there aren’t any other rules for the same state and top-of-stack character, because
that would create an ambiguity about whether or not a character should be read from the
input.
DFAs also have a “no omissions” constraint—there should be a rule for every possible
situation—but that idea becomes unwieldy for DPDAs because of the large number of possible
combinations of state, input character, and top-of-stack character. It’s conventional to
just ignore this constraint and allow DPDAs to specify only the interesting rules that they
need to get their job done, and assume that a DPDA will go into an implicit
stuck
state
if it gets into a situation where none of its rules apply. This is what
happens to our balanced-brackets DPDA when it reads a string like')'or'())', because there’s no rule for
reading a closing bracket while in state 1.
Now that we’ve dealt
with the technical details, let’s build a Ruby simulation
of a deterministic pushdown automaton so we can interact with it. We
already did most of the hard work when we simulated DFAs and NFAs, so
this’ll just take a bit of fine-tuning.
The most important thing we’re missing is a stack. Here’s one way
of implementing aStackclass:
classStack<Struct.new(:contents)defpush(character)Stack.new([character]+contents)enddefpopStack.new(contents.drop(1))enddeftopcontents.firstenddefinspect"##{top})#{contents.drop(1).join}>"endend
AStackobject stores its
contents in an underlying array and exposes simple#pushand#popoperations to push characters onto the
stack and pop them off, plus a#topoperation to read the character at the top of the stack:
>>stack=Stack.new(['a','b','c','d','e'])=> #>>stack.top=> "a">>stack.pop.pop.top=> "c">>stack.push('x').push('y').top=> "y">>stack.push('x').push('y').pop.top=> "x"
This is a
purely functional
stack. The#pushand#popmethods are nondestructive: they each
return a newStackinstance rather
than modifying the existing one. Creating a new object every time
makes this implementation less efficient than a conventional stack
with destructive#pushand#popoperations (and we could just useArraydirectly if we wanted that)
but also makes it easier to work with, because we don’t need to worry
about the consequences of modifying aStackthat’s being used in more than one
place.
In
Chapter 3
, we saw that we can simulate a deterministic
finite automaton by keeping track of just one piece of information—the DFA’s current
state—and then using the
rulebook to update that information each time a character is read from the
input. But there are
two
important things to know about a pushdown
automaton at each step of its computation: what its current state is, and what the current
contents of its stack are. If we use the word
configuration
to refer
to this combination of a state and a stack, we can talk about a pushdown automaton moving
from one configuration to another as it reads input characters, which is easier than always
having to refer to the state and stack separately. Viewed this way, a DPDA just has a
current configuration, and the rulebook tells us how to turn the current configuration into
the next configuration each time we read a character.
Here’s aPDAConfigurationclass
to hold the configuration of a PDA—a state and a stack—and aPDARuleclass to represent one rule in a PDA’s
rulebook:
[
33
]
classPDAConfiguration<Struct.new(:state,:stack)endclassPDARule<Struct.new(:state,:character,:next_state,:pop_character,:push_characters)defapplies_to?(configuration,character)self.state==configuration.state&&self.pop_character==configuration.stack.top&&self.character==characterendend
A rule only applies when the machine’s state, topmost stack
character, and next input character all have the values it
expects:
>>rule=PDARule.new(1,'(',2,'$',['b','$'])=> #state=1,character="(",next_state=2,pop_character="$",push_characters=["b", "$"]>>>configuration=PDAConfiguration.new(1,Stack.new(['$']))=> #> >>rule.applies_to?(configuration,'(')=> true
For a finite automaton, following a rule just means changing from
one state to another, but a PDA rule updates the stack contents as well
as the state, soPDARule#followneeds
to take the machine’s current configuration as an argument and return
the next one:
classPDARuledeffollow(configuration)PDAConfiguration.new(next_state,next_stack(configuration))enddefnext_stack(configuration)popped_stack=configuration.stack.poppush_characters.reverse.inject(popped_stack){|stack,character|stack.push(character)}endend
If we push several characters onto a stack and then pop them
off, they come out in the opposite order:
>>stack=Stack.new(['$']).push('x').push('y').push('z')=> #>>stack.top=> "z">>stack=stack.pop;stack.top=> "y">>stack=stack.pop;stack.top=> "x"
PDARule#next_stackanticipates this by reversing thepush_charactersarray before pushing its
characters onto the stack. For example, the last character inpush_charactersis the actually the
first
one to be pushed onto the stack, so it’ll
be the last to be popped off again. This is just a convenience so that
we can read a rule’spush_charactersas the sequence of
characters (in “popping order”) that will be on top of the stack after
the rule is applied, without having to worry about the mechanics of
how they get on there.
So, if we have aPDARulethat
applies to aPDAConfiguration, we can
follow it to find out what the next state and stack will be:
>>rule.follow(configuration)=> #>
This gives us enough to implement a rulebook for DPDAs. The
implementation is very similar to theDFARulebookfrom
Simulation
:
classDPDARulebook<Struct.new(:rules)defnext_configuration(configuration,character)rule_for(configuration,character).follow(configuration)enddefrule_for(configuration,character)rules.detect{|rule|rule.applies_to?(configuration,character)}endend
Now we can assemble the rulebook for the balanced-brackets DPDA
and try stepping through a few configurations and input characters by
hand:
>>rulebook=DPDARulebook.new([PDARule.new(1,'(',2,'$',['b','$']),PDARule.new(2,'(',2,'b',['b','b']),PDARule.new(2,')',2,'b',[]),PDARule.new(2,nil,1,'$',['$'])])=> #>>configuration=rulebook.next_configuration(configuration,'(')=> #> >>configuration=rulebook.next_configuration(configuration,'(')=> #> >>configuration=rulebook.next_configuration(configuration,')')=> #>
