Understanding Computation (21 page)

That’s great, but themin the
middle of the input string is a cop-out. Why can’t we design a machine
that just recognizes palindromes—aa,abba,babbaabbab, etc.—without having to put a marker
halfway through?
The machine has to change from state 1 to state 2 as soon as it reaches the halfway point
of the string, and without a marker, it has no way of knowing when to do that. As we’ve seen
before with NFAs, these “how do I know when to…?” problems can be solved by relaxing the
determinism constraints and allowing the machine the freedom to make that vital state change
at any point, so that it’s
possible
for it to accept a palindrome by
following the right rule at the right time.
Unsurprisingly, a pushdown automaton without determinism constraints
is called a
nondeterministic pushdown automaton
.
Here’s one for recognizing palindromes with an even number of
letters:
[
34
]
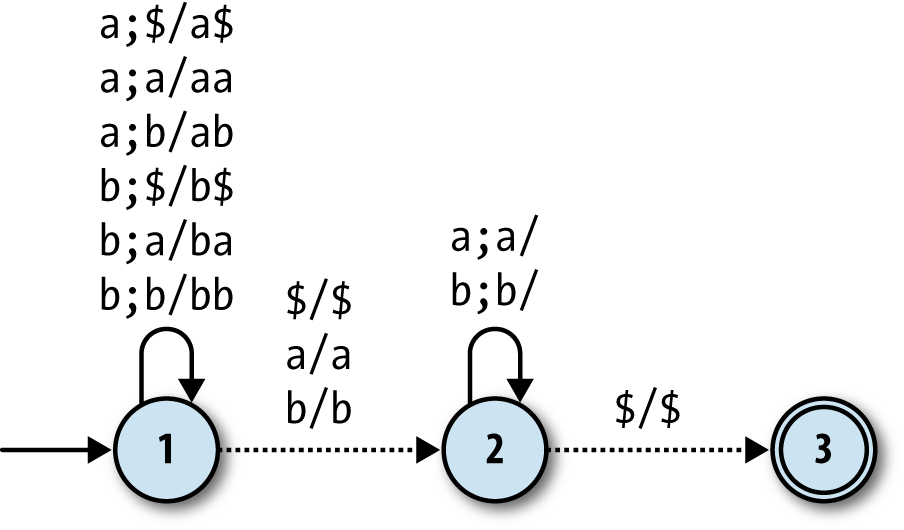
This is identical to the DPDA version except for the rules that lead from state 1 to state
2: in the DPDA, they read anmfrom the input, but here
they’re free moves. This gives the NPDA the opportunity to change state anywhere during the
input string without needing a
marker.
A nondeterministic
machine is more difficult to simulate than a deterministic
one, but we’ve already done the hard work for NFAs in
Nondeterminism
, and we can reuse the same ideas for NPDAs.
We need anNPDARulebookfor holding a
nondeterministic collection ofPDARules, and its implementation is almost
exactly the same asNFARulebook:
require'set'classNPDARulebook<Struct.new(:rules)defnext_configurations(configurations,character)configurations.flat_map{|config|follow_rules_for(config,character)}.to_setenddeffollow_rules_for(configuration,character)rules_for(configuration,character).map{|rule|rule.follow(configuration)}enddefrules_for(configuration,character)rules.select{|rule|rule.applies_to?(configuration,character)}endend
In
Nondeterminism
, we simulated an NFA by keeping track of aSetof possible states; here we’re simulating an NPDA with aSetof possible
configurations
.
Our rulebook needs the usual support for free moves, again
virtually identical toNFARulebook’s
implementation:
classNPDARulebookdeffollow_free_moves(configurations)more_configurations=next_configurations(configurations,nil)ifmore_configurations.subset?(configurations)configurationselsefollow_free_moves(configurations+more_configurations)endendend
And we need anNPDAclass to
wrap up a rulebook alongside theSetof current configurations:
classNPDA<Struct.new(:current_configurations,:accept_states,:rulebook)defaccepting?current_configurations.any?{|config|accept_states.include?(config.state)}enddefread_character(character)self.current_configurations=rulebook.next_configurations(current_configurations,character)enddefread_string(string)string.chars.eachdo|character|read_character(character)endenddefcurrent_configurationsrulebook.follow_free_moves(super)endend
This lets us step through a simulation of all possible
configurations of an NPDA as each character is read:
>>rulebook=NPDARulebook.new([PDARule.new(1,'a',1,'$',['a','$']),PDARule.new(1,'a',1,'a',['a','a']),PDARule.new(1,'a',1,'b',['a','b']),PDARule.new(1,'b',1,'$',['b','$']),PDARule.new(1,'b',1,'a',['b','a']),PDARule.new(1,'b',1,'b',['b','b']),PDARule.new(1,nil,2,'$',['$']),PDARule.new(1,nil,2,'a',['a']),PDARule.new(1,nil,2,'b',['b']),PDARule.new(2,'a',2,'a',[]),PDARule.new(2,'b',2,'b',[]),PDARule.new(2,nil,3,'$',['$'])])=> #>>configuration=PDAConfiguration.new(1,Stack.new(['$']))=> #> >>npda=NPDA.new(Set[configuration],[3],rulebook)=> #>>npda.accepting?=> true>>npda.current_configurations=> ##>, #>, #> }>>>npda.read_string('abb');npda.accepting?=> false>>npda.current_configurations=> ##>, #>, #> }>>>npda.read_character('a');npda.accepting?=> true>>npda.current_configurations=> ##>, #>, #>, #> }>
And finally anNPDADesignclass
for testing strings directly:
classNPDADesign<Struct.new(:start_state,:bottom_character,:accept_states,:rulebook)defaccepts?(string)to_npda.tap{|npda|npda.read_string(string)}.accepting?enddefto_npdastart_stack=Stack.new([bottom_character])start_configuration=PDAConfiguration.new(start_state,start_stack)NPDA.new(Set[start_configuration],accept_states,rulebook)endend
Now we can check that our NPDA actually does recognize
palindromes:
>>npda_design=NPDADesign.new(1,'$',[3],rulebook)=> #>>npda_design.accepts?('abba')=> true>>npda_design.accepts?('babbaabbab')=> true>>npda_design.accepts?('abb')=> false>>npda_design.accepts?('baabaa')=> false
