Understanding Computation (23 page)

This execution trace shows us how the machine ping-pongs between
symbol and token rules: the symbol rules repeatedly expand the symbol on
the top of the stack until it gets replaced by a token, then the token
rules consume the stack (and the input) until they hit a symbol. This
back and forth eventually results in an empty stack as long as the input
string can be generated by the grammar rules.
[
36
]
How does the PDA know which rule to choose at each step of
execution? Well, that’s the power of nondeterminism: our NPDA simulation
tries all possible rules, so as long as there’s
some
way of getting to an empty stack,
we’ll find it.
This parsing
procedure relies on nondeterminism, but in real applications, it’s best to avoid
nondeterminism, because a deterministic PDA is much faster and easier to simulate than a
nondeterministic one. Fortunately, it’s almost always possible to eliminate nondeterminism
by using the input tokens themselves to make decisions about which symbol rule to apply at
each stage—a
technique called
lookahead
—but that makes the translation
from CFG to PDA more complicated.
It’s also not really good enough to only be able to
recognize
valid
programs. As we saw in
Implementing Parsers
, the whole point of parsing a
program is to turn it into a structured representation that we can then do something useful
with. In practice, we can create this representation by instrumenting our PDA simulation to
record the sequence of rules it follows to reach an accept state, which provides enough
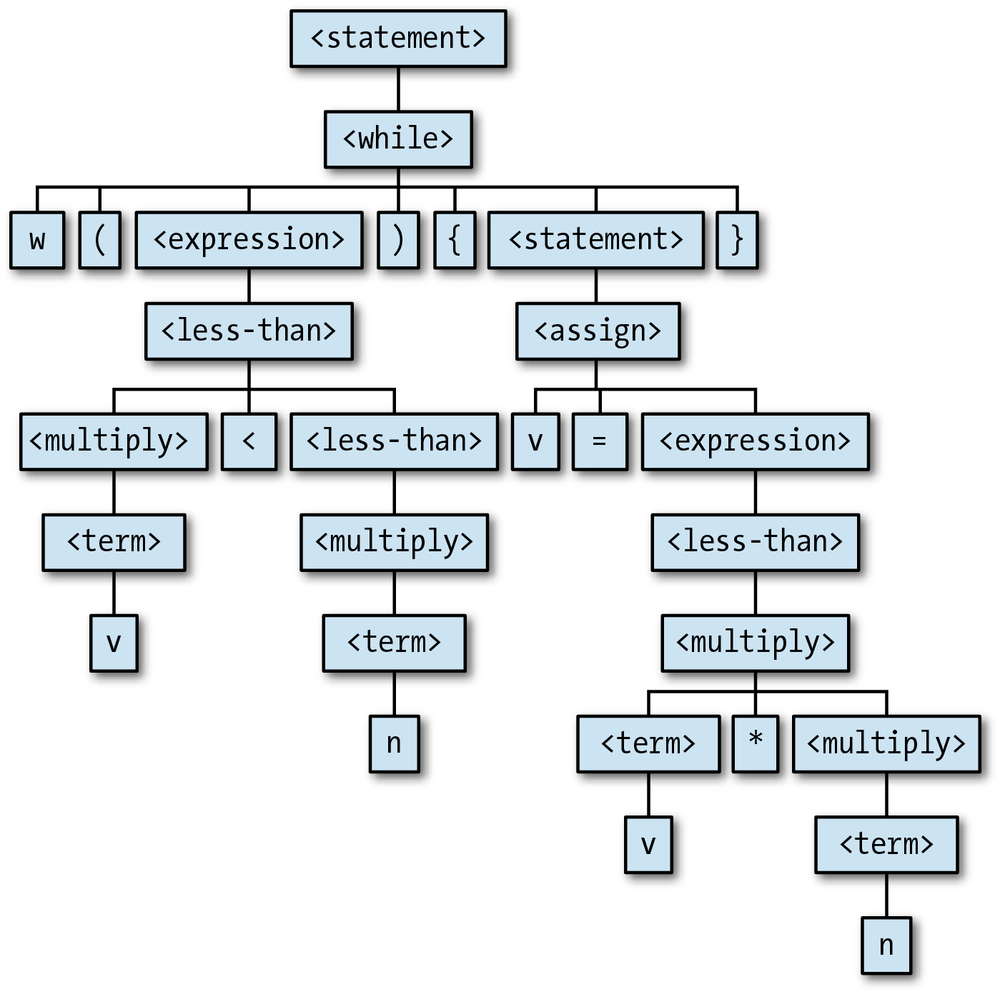
information to construct a parse tree. For example, the above execution trace shows us how
the symbols on the stack get expanded to form the desired sequence of tokens, and that tells
us the shape of the parse tree for the
string'w(v:
In this chapter, we’ve encountered
two new levels of computing power: DPDAs are more powerful than DFAs and NFAs, and
NPDAs are more powerful again. Having access to a stack, it seems, gives pushdown automata a
bit more power and sophistication than finite automata.
The main consequence of having a stack is the ability to recognize
certain languages that finite automata aren’t capable of recognizing, like
palindromes and strings of balanced brackets. The unlimited storage
provided by a stack lets a PDA remember arbitrary amounts of information
during a computation and refer back to it later.
Unlike finite automata, a PDA can loop indefinitely without reading
any input, which is curious even if it’s not particularly useful. A DFA
can only ever change state by consuming a character of input, and although
an NFA can change state spontaneously by following a free move, it can
only do that a finite number of times before it ends up back where it
started. A PDA, on the other hand, can sit in a single state and keep
pushing characters onto its stack forever, never once repeating the same
configuration.
Pushdown automata can also control themselves to a limited extent.
There’s a feedback loop between the rules and the stack—the contents of
the stack affect which rules the machine can follow, and following a rule
will affect the stack contents—which allows a PDA to store away
information on the stack that will influence its future execution. Finite
automata rely upon a similar feedback loop between their rules and current
state, but the feedback is less powerful because the current state is
completely forgotten when it changes, whereas pushing characters onto a
stack preserves the old contents for later use.
Okay, so PDAs are a bit more powerful, but what are their limitations? Even if we’re only
interested in the kinds of pattern-matching applications we’ve already seen, pushdown automata
are still seriously limited by the way a stack works. There’s no random access to stack
contents below the topmost character, so if a machine wants to read a character that’s buried
halfway down the stack, it has to pop everything above it. Once characters have been popped,
they’re gone forever; we designed a PDA to recognize strings with equal numbers ofas andbs, but we can’t adapt
it to recognize strings with equal numbers of
three
different types of
character ('abc','aabbcc','aaabbbccc', …) because the
information about the number ofas gets destroyed by the
process of counting thebs.
Aside from the
number
of times that pushed characters can be used,
the last-in-first-out nature of a stack causes a problem with the
order
in which information is stored and retrieved. PDAs can recognize palindromes, but they can’t
recognize doubled-up strings like'abab'and'baaabaaa', because once information has been pushed onto a stack,
it can only be consumed in reverse order.
If we move away from the specific problem of recognizing strings and
try to treat these machines as a model of general-purpose computers, we
can see that DFAs, NFAs, and PDAs are still a long way from being properly
useful. For starters, none of them has a decent output mechanism: they can
communicate success by going into an accept state, but can’t output even a
single character (much less a whole string of characters) to indicate a
more detailed result. This inability to send information back out into the
world means that they can’t implement even a simple algorithm like adding
two numbers together. And like finite automata, an individual PDA has a
fixed program; there isn’t an obvious way to build a PDA that can somehow
read a program from its input and run it.
All of these weaknesses mean that we need a better model of
computation to really investigate what computers are capable of, and
that’s exactly what the
next
chapter
is about.
[
29
]
This isn’t quite the same as accepting strings that merely contain equal numbers of
opening and closing brackets. The strings'()'and')('each contain a single opening and closing bracket,
but only'()'is balanced.
[
30
]
This doesn’t mean that an input string can ever actually be infinite, just that we can
make it as finitely large as we like.
[
31
]
Briefly, this algorithm works by converting an NFA into a
generalized
nondeterministic finite automaton
(GNFA), a finite state machine where each
rule is labeled with a regular expression instead of a single character, and then
repeatedly merging the states and rules of the GNFA until there are only two states and
one rule left. The regular expression that labels that final rule always matches the same
strings as the original NFA.
[
32
]
Of course, any real-world implementation of a stack is always going to be limited by
the size of a computer’s RAM, or the free space on its hard drive, or the number of
atoms in the universe, but for the purposes of our thought experiment, we’ll assume that
none of those constraints exist.
[
33
]
These class names begin withPDA, rather thanDPDA, because their implementations don’t
make any assumptions about determinism, so they’d work just as well
for simulating a nondeterministic PDA.
[
34
]
The “even number of letters” restriction keeps the machine
simple: a palindrome of length2ncan be accepted
by pushingncharacters onto the stack and then
poppingncharacters off. To recognize
any
palindrome requires a few more rules going
from state 1 to state 2.
[
35
]
The grammar is “context free” in the sense that its rules don’t say anything about
the context in which each piece of syntax may appear; an assignment statement
always
consists of a variable name, equals sign, and expression,
regardless of what other tokens surround it. Not all imaginable languages can be
described by this kind of grammar, but almost all programming languages can.
[
36
]
This algorithm is called
LL parsing
. The first L stands for
“left-to-right,” because the input string is read in that direction, and the second L
stands for “left derivation,” because it’s always the leftmost (i.e., uppermost) symbol
on the stack that gets expanded.
In
Chapter 3
and
Chapter 4
, we
investigated the capabilities of simple models of computation. We’ve seen how to recognize
strings of increasing complexity, how to match regular expressions, and how to parse programming
languages, all using basic machines with very little complexity.
But we’ve also seen that these machines—finite automata and pushdown automata—come with
serious limitations that undermine their usefulness as realistic models of computation. How much
more powerful do our toy systems need to get before they’re able to escape these limitations and
do everything that a normal computer can do? How much more complexity is required to model the
behavior of RAM, or a hard drive, or a proper output mechanism? What does it take to design a
machine that can actually
run programs
instead of always executing a single
hardcoded task?
In the 1930s, Alan Turing
was working on essentially this problem. At that time, the word “computer” meant a
person, usually a woman, whose job was to perform long calculations by repeating a series of
laborious mathematical operations by hand. Turing was looking for a way to understand and
characterize the operation of a human computer so that the same tasks could be performed
entirely by machines. In this chapter, we’ll look at Turing’s revolutionary ideas about how to
design the simplest possible “automatic machine” that captures the full power and complexity of
manual computation.
In
Chapter 4
, we
were able to increase the computational power of a finite automaton by giving it a
stack to use as
external memory. Compared to the finite internal memory provided by a machine’s
states, the real advantage of a stack is that it can grow dynamically to accommodate any
amount of information, allowing a pushdown automaton to handle problems where an arbitrary
amount of data needs to be stored.
However, this particular form of external memory imposes
inconvenient limitations on how data can be used after it’s been stored.
By replacing the stack with a more flexible storage mechanism, we can
remove those limitations and achieve another increase in power.
Computing is normally done by writing certain symbols on paper.
We may suppose this paper is divided into squares like a child’s
arithmetic book. In elementary arithmetic the two-dimensional
character of the paper is sometimes used. But such a use is always
avoidable, and I think that it will be agreed that the two-dimensional
character of paper is no essential of computation. I assume then that
the computation is carried out on one-dimensional paper, i.e. on a
tape divided into squares.
Turing’s
solution was to equip a
machine with a blank tape of unlimited length—effectively
a one-dimensional array that can grow at both ends as needed—and allow
it to read and write characters anywhere on the tape. A single tape
serves as both storage and input: it can be prefilled with a string of
characters to be treated as input, and the machine can read those
characters during execution and overwrite them if necessary.
A finite state machine with access to an infinitely long tape is
called a
Turing machine
(TM). That name usually
refers to a machine with deterministic rules, but we can also call it a
deterministic Turing machine
(DTM) to be
completely unambiguous.
We already know that a pushdown automaton can only access a single fixed location in its
external storage—the top of the stack—but that seems too restrictive for a Turing machine.
The whole point of providing a tape is to allow arbitrary amounts of data to be stored
anywhere on it and read off again in any order, so how do we design a machine that can
interact with the entire length of its tape?
One option is make the tape addressable by random access, labeling
each square with a unique numerical address like computer RAM, so that
the machine can immediately read or write any location. But that’s more
complicated than strictly necessary, and requires working out details
like how to assign addresses to all the squares of an infinite tape and
how the machine should specify the address of the square it wants to
access.
Instead, a conventional Turing machine uses a simpler arrangement: a
tape
head
that points at a specific position on the tape and can only read or write
the character at that position. The tape head can move left or right by a single square
after each step of computation, which means that a Turing machine has to move its head
laboriously back and forth over the tape in order to reach distant locations. The use of a
slow-moving head doesn’t affect the machine’s ability to access any of the data on the tape,
only the amount of time it takes to do it, so it’s a worthwhile trade-off for the sake of
keeping things simple.
Having access to a tape allows us to solve new kinds of problems beyond simply accepting
or rejecting strings. For example, we can design a DTM for incrementing a binary number
in-place on the tape. To do this, we need to know how to increment a single
digit
of a binary number, but fortunately, that’s easy: if the digit
is a zero, replace it with a one; if the digit is a one, replace it with a zero, then
increment the digit immediately to its left (“carry the one”) using the same technique. The
Turing machine just has to use this procedure to increment the binary number’s rightmost
digit and then return the tape head to its starting position:
Give the machine three states, 1, 2 and 3, with state 3 being the accept
state.Start the machine in state 1 with the tape head positioned over the rightmost digit
of a binary number.When in state 1 and a zero (or blank) is read, overwrite it with a one, move the
head right, and go into state 2.When in state 1 and a one is read, overwrite it with a zero and move the head
left.When in state 2 and a zero or one is read, move the head right.
When in state 2 and a blank is read, move the head left and go into state 3.
This machine is in state 1 when it’s trying to increment a digit, state 2 when it’s
moving back to its starting position, and state 3 when it has finished. Below is a trace of
its execution when the initial tape contains the string'1011'; the character currently underneath the tape head is shown surrounded by
brackets, and the underscores represent the blank squares on either side of the input
string.
| State | Accepting? | Tape contents | Action |
| 1 | no | _101(1)__ | write0, moveleft |
| 1 | no | __10(1)0_ | write0, moveleft |
| 1 | no | ___1(0)00 | write1, move right,go to state 2 |
| 2 | no | __11(0)0_ | move right |
| 2 | no | _110(0)__ | move right |
| 2 | no | 1100(_)__ | move left, go to state 3 |
| 3 | yes | _110(0)__ | — |
Moving the tape head back to its initial position isn’t strictly necessary—if we made
state 2 an accept state, the machine would halt immediately once it had successfully
replaced a zero with a one, and the tape would still contain the correct result—but it’s a
desirable feature, because it leaves the head in a position where the machine can be run
again by simply changing its state back to 1. By running the machine several times, we can
repeatedly increment the number stored on the tape. This functionality could be reused as
part of a larger machine for, say, adding or multiplying two binary numbers.
Let us imagine the operations performed by the computer to be
split up into “simple operations” that are so elementary that it is
not easy to imagine them further divided. […] The operation actually
performed is determined […] by the state of mind of the computer and
the observed symbols. In particular, they determine the state of mind
of the computer after the operation is carried out.We may now construct a machine to do the work of this
computer.—
Alan Turing,
On Computable Numbers, with an Application to the
Entscheidungsproblem
There are
several “simple operations” we might want a Turing machine
to perform in each step of computation: read the character at the tape
head’s current position, write a new character at that position, move
the head left or right, or change state. Instead of having different
kinds of rule for all these actions, we can keep things simple by
designing a single format of rule that is flexible enough for every
situation, just as we did for pushdown automata.
This unified rule format has five parts:
The current state of the machine
The character that must appear at the tape head’s current position
The next state of the machine
The character to write at the tape head’s current position
The direction (left or right) in which to move the head after writing to the
tape
Here we’re making the assumption that a Turing machine will change state and write a
character to the tape every time it follows a rule. As usual for a state machine, we can
always make the “next state” the same as the current one if we want a rule that doesn’t
actually change state; similarly, if we want a rule that doesn’t change the tape contents,
we can just use one that writes the same character that it reads.
We’re also assuming that the tape head always moves at every step. This makes it
impossible to write a single rule that updates the state or the tape contents without
moving the head, but we can get the same effect by writing one rule that makes the desired
change and another rule that moves the head back to its original position
afterward.
The Turing machine for incrementing a binary number has six rules
when they’re written in this style:
When in state 1 and a zero is read, write a one, move right, and go into state
2.When in state 1 and a one is read, write a zero, move left, and stay in state
1.When in state 1 and a blank is read, write a one, move right, and go into state
2.When in state 2 and a zero is read, write a zero, move right, and stay in state
2.When in state 2 and a one is read, write a one, move right, and stay in state
2.When in state 2 and a blank is read, write a blank, move left, and go into state
3.
We can show this machine’s states and rules on a diagram similar
to the ones we’ve already been using for finite and pushdown
automata:
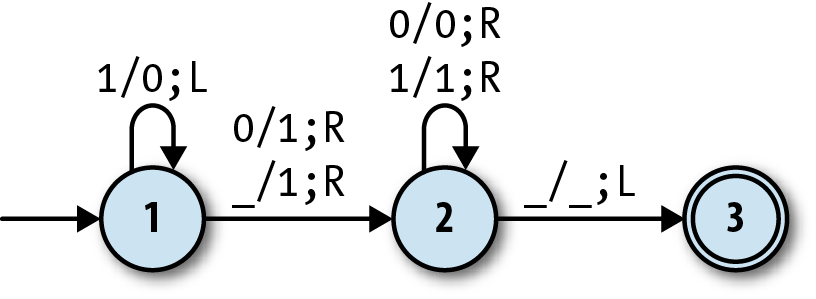
In fact, this is just like a DFA diagram except for the labels on
the arrows. A label of the forma/b;Lindicates a rule that reads characterafrom the tape, writes characterb, and then moves the tape head one square to
the left; a rule labelleda/b;Rdoes
almost the same, but moves the head to the right instead of the
left.
Let’s see how to use a Turing machine to solve a string-recognition problem that
pushdown automata can’t handle: identifying inputs that consist of one or moreacharacters followed by the same number ofbs andcs (e.g.,'aaabbbccc'). The Turing machine that solves this problem has 6
states and 16 rules:
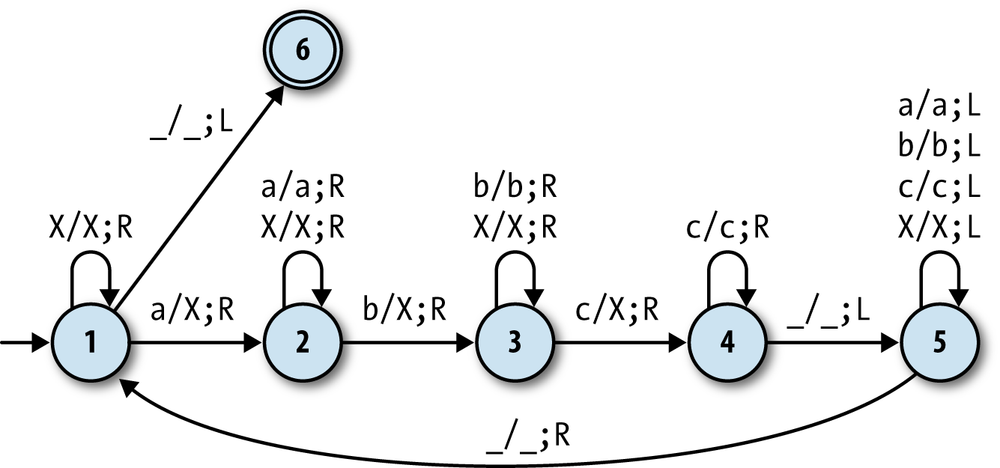
It works roughly like this:
Scan across the input string by repeatedly moving the tape
head to the right until anais
found, then cross it out by replacing it with anX(state 1).Scan right looking for a
b,
then cross it out (state 2).Scan right looking for a
c,
then cross it out (state 3).Scan right looking for the end of the input string (state 4),
then scan left looking for the beginning (state 5).Repeat these steps until all characters have been crossed
out.
If the input string consists of one or moreacharacters followed by the same number ofbs andcs, the machine will make repeated passes across the whole
string, crossing out one of each character on every pass, and then enter an accept state
when the entire string has been crossed out. Here’s a trace of its execution when the input
is'aabbcc':
| State | Accepting? | Tape contents | Action |
| 1 | no | ______(a)abbcc_ | writeX, move right,go to state 2 |
| 2 | no | _____X(a)bbcc__ | move right |
| 2 | no | ____Xa(b)bcc___ | writeX, move right,go to state 3 |
| 3 | no | ___XaX(b)cc____ | move right |
| 3 | no | __XaXb(c)c_____ | writeX, move right,go to state 4 |
| 4 | no | _XaXbX(c)______ | move right |
| 4 | no | XaXbXc(_)______ | move left, go to state 5 |
| 5 | no | _XaXbX(c)______ | move left |
| 5 | no | __XaXb(X)c_____ | move left |
| 5 | no | ___XaX(b)Xc____ | move left |
| 5 | no | ____Xa(X)bXc___ | move left |
| 5 | no | _____X(a)XbXc__ | move left |
| 5 | no | ______(X)aXbXc_ | move left |
| 5 | no | ______(_)XaXbXc | move right, go to state 1 |
| 1 | no | ______(X)aXbXc_ | move right |
| 1 | no | _____X(a)XbXc__ | writeX, move right,go to state 2 |
| 2 | no | ____XX(X)bXc___ | move right |
| 2 | no | ___XXX(b)Xc____ | writeX, move right,go to state 3 |
| 3 | no | __XXXX(X)c_____ | move right |
| 3 | no | _XXXXX(c)______ | writeX, move right,go to state 4 |
| 4 | no | XXXXXX(_)______ | move left, go to state 5 |
| 5 | no | _XXXXX(X)______ | move left |
| 5 | no | __XXXX(X)X_____ | move left |
| 5 | no | ___XXX(X)XX____ | move left |
| 5 | no | ____XX(X)XXX___ | move left |
| 5 | no | _____X(X)XXXX__ | move left |
| 5 | no | ______(X)XXXXX_ | move left |
| 5 | no | ______(_)XXXXXX | move right, go to state 1 |
| 1 | no | ______(X)XXXXX_ | move right |
| 1 | no | _____X(X)XXXX__ | move right |
| 1 | no | ____XX(X)XXX___ | move right |
| 1 | no | ___XXX(X)XX____ | move right |
| 1 | no | __XXXX(X)X_____ | move right |
| 1 | no | _XXXXX(X)______ | move right |
| 1 | no | XXXXXX(_)______ | move left, go to state 6 |
| 6 | yes | _XXXXX(X)______ | — |
This machine works because of the exact choice of rules during the scanning stages. For
example, while the machine is in state 3—scanning right and looking for ac—it only has rules for moving the head pastbs andXs. If it hits some
other character (e.g., an unexpecteda), then it has no
rule to follow, in which case it’ll go into an implicit stuck state and stop executing,
thereby rejecting that input.
We’re keeping things simple by assuming that the input can only ever contain the
charactersa,b, andc, but this machine won’t work properly if that’s not
true; for example, it will accept the string'XaXXbXXXc'even though it should be rejected. To correctly handle that sort
of input, we’d need to add more states and rules that scan over the whole string to check
that it doesn’t contain any unexpected characters before the machine starts crossing
anything off.
