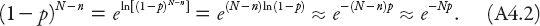X and the City: Modeling Aspects of Urban Life (78 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Of course, there are potentially an infinite number of distance metrics and corresponding “circles.” The metric (or formula) for the distance of a point (
x, y
) from the origin in Euclidean geometry is of course well known: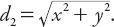 This is readily generalized for other positive integers
This is readily generalized for other positive integers
n
such that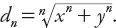 The case for taxicab geometry corresponds to
The case for taxicab geometry corresponds to
n
= 1, for which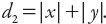 As
As
n
increases in value, the “circles” become more and more bulbous, as seen in
Figure A3.1
for several values of
n
, and in the limit as
n
→ ∞, the metric is defined to be
d
∞
= max{|
x
|,|
y
|}. As can be seen from the figure, the unit circle for the
d
∞
metric is a square with sides parallel to the coordinate axes.
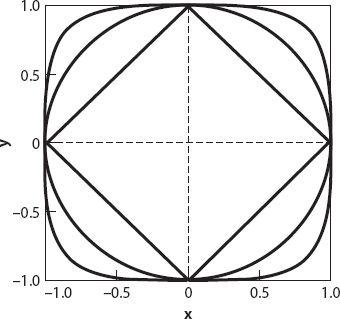
Figure A3.1. Taxicab “circles”
d
1
,
d
2
,
d
4
, and
d
∞
.
Exercise 1:
Mark the points
A
= (−2, −1) and
B
= (2, 2) on a piece of graph paper. Then sketch the locus of all points P such that
d
T
(
P
,
A
) +
d
T
(
P
,
B
) = 9. By analogy with the corresponding figure in Euclidean geometry provide a name for this figure.
Exercise 2:
Mark the points
A
= (−3, −1) and
B
= (2, 2) on a piece of graph paper. Then sketch the locus of all points
P
such that |
d
T
(
P
,
A
) −
d
T
(
P
,
B
)| = 3. Again, by analogy with the corresponding figure in Euclidean geometry provide a name for this figure.
THE POISSON DISTRIBUTION
Applications of the Poisson distribution are many and varied. A large class of natural and social phenomena have been successfully modeled using it [45]. Before deriving the formula for this distribution let’s consider some examples. A classic one concerns a Russian statistician, Ladislaus Bortkiewicz, who used the Poisson distribution to estimate the number of soldiers killed by mule-kicks to the head in the Prussian army. He assembled data on the 14 cavalry corps over a period of 20 years, and in so doing he was able to verify that the distribution of mule-kick deaths fit a Poisson distribution! Another example is the number of armadillos killed by traffic on a length of an Arizona highway; this is also “Poisson distributed.” Other examples are the number of emergency room cases cases arriving at a hospital during a one-hour period, and the number of bomb hits in one-acre areas of metropolitan London during World War II [
45
]. More pedestrian examples include the number of times I check my email in the morning, the number of cars that pass a particular “eatery” in a two-hour period (perhaps the “
Road-Kill Café
” in a certain Arizona town?).
This is not of course to imply that everything can or should be modeled as a Poisson process, however; there are certain restrictions that must be satisfied before the phenomenon of interest can be thus described. The ER cases arriving on a Sunday morning would probably not have the same distribution as those on a Saturday evening, for example. Also, if there were an explosion or tornado, the arrivals would be associated with a common cause, and this could render the Poisson distribution inappropriate. If the area of London were extended too far into the surrounding countryside, the intensity of the bomb damage would be much less severe. The armadillos are presumed to cross the highway at random locations, not to be traveling as a herd, or in convoy, or crossing the road at a particular spot (as Canada geese seem to do, especially when I am in a hurry).
Perhaps the simplest context in which to place the mathematical discussion is found by asking the following question. What is the probability of getting exactly
n
tails in
N
tosses of a (possibly unfair) coin, where
n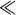 N
N
? This means that there will be
N
−
n
heads, of course, and if the probability of getting a tail is
p
, then that of getting a head is 1 −
p
. Of course, if the coin is fair, then
p
= 1/2. The probability of
n
tails is therefore the number of ways one can have
n
tails in
N
tosses multiplied by the probabilities associated with each toss. The result is
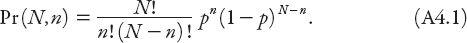
This is known as the binomial probability distribution. To obtain the Poisson distribution as a limiting case of this distribution we suppose getting a tail is a very rare event, that is,
p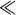 1; this corresponds to a very unfair coin! We can (eventually) simplify expression (A4.1). First, we note that for
1; this corresponds to a very unfair coin! We can (eventually) simplify expression (A4.1). First, we note that for
p 1, ln(1 −
1, ln(1 −
p
) ≈
p
, so that