A Player's Guide to Chords and Harmony (9 page)

STACKING INTERVALS

Already in this book you've seen a number of references to stacking intervals - placing one on top of another. The concept is simple, but a clear explanation won't hurt. When two intervals are stacked, the top note of the lower interval is the same as the bottom note of the upper interval. A few examples of stacked intervals are shown in Figure 2-8.

Figure 2-8. Two intervals can be stacked by using the upper note of the first interval as the lower note of the second interval.

As an exercise, you might want to choose a relatively large interval, such as a 5th or 6th, and work out which combinations of smaller intervals can be stacked to produce the larger interval. I've done this with the minor 6th in Figure 2-9. It's easy to do: Simply play the large interval on the keyboard, play any note between the two notes of the interval, and observe the intervals that this inner note forms with the outer two notes. In this case you're splitting an interval rather than stacking two intervals, but the results are the same.

Figure 2-9. Any interval larger than a minor 2nd can be analyzed as two stacked intervals. Here are the primary ways of producing a minor 6th by stacking intervals. (Options such as C-D#-A6, which contain doubly diminished or doubly augmented intervals, have been omitted.)

INVERTED INTERVALS

Generally, it's convenient to talk about intervals by stating the lower note first. When I refer to the interval C-G, for instance, you can safely assume that the C is below the G. But what about the interval G-C? Although the C is an octave higher than before, G-C contains the same two notes as C-G. But as Figure 2-10 makes clear, C-G is a perfect 5th, while G-C is a perfect 4th.

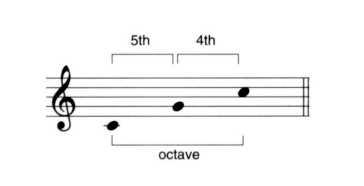
Figure 2-10. The interval C-G is not the same as the interval G-C.

These two intervals have a special relationship: The perfect 4th is called an inversion of the perfect 5th, and vice-versa. Another way to say this is that if we invert a perfect 5th by moving the lower note up an octave, we get a perfect 4th. We'll return to the subject of inversions in Chapter Three. In general, moving the bottom note of a chord or interval up by an octave (or, if necessary, two octaves) so that it's at the top produces an inversion. Likewise, moving the top note down by one or more octaves so that it's at the bottom inverts the chord or interval.

Any pair of intervals that, when stacked, produce a perfect octave are inversions of one another. When two intervals have this relationship, we can also say they're complementary or reciprocal with respect to one another. The most important pairs of reciprocal intervals are shown in Figure 2-11. As you study this figure, you'll notice that inverting a minor interval always produces a major interval, and vice-versa. Inverting an augmented interval produces a diminished interval, and vice-versa. Inverting a perfect interval produces another perfect interval.

The pairing of reciprocal intervals is important because inverting an interval leaves its harmonic identity and harmonic function intact. In other words, it sounds pretty much the same as it did before. You can verify this at the keyboard. Play the interval C-E, preferably by striking both notes at the same time. Then raise the C by an octave and play E-C in the same manner. Notice how similar the two intervals sound. In many situations, you can invert an interval in this way without changing the harmonic meaning of the passage. The sound will be slightly different, but the harmonic function of the chord that contains the interval will most often be exactly the same. (Figure 6-11 in Chapter Six provides a couple of examples of chords to which this rule doesn't apply.)

Figure 2-11. When two intervals can be stacked to form a perfect octave, we say that each interval is the inversion of the other

SOUND COLORS

Each interval has a distinctive sound. And because music can express emotions, it's possible to describe the sounds of intervals in words. While there's not a complete consensus among listeners, many people would subscribe to some or all of the following descriptions:

In classical music theory, intervals are also classified as consonant or dissonant. A dissonant interval is one that is harsh-sounding or unsettled. A consonant interval is felt to be solid and stable. The classification of intervals as consonant or dissonant has changed over the centuries, however. In the Medieval and Renaissance periods, it was felt that the only consonant intervals were the unison, perfect 5th, and octave. Major and minor 3rds and 6ths were felt to be dissonant. Music from this period is full of 3rds and 6ths, but the final cadence (the end of the piece) typically ends with a chord consisting only of octaves and perfect 5ths, because composers felt that this ending was necessary in order to resolve the dissonances into consonances.

In the Baroque and Classical periods (roughly 1600-1820), listeners became comfortable accepting the major 3rd as a consonance, but the minor 3rd was still felt to be somewhat dissonant. As a result, pieces written in minor keys often ended in a major key, so that the 3rd of the final chord would be major, not minor. By the Romantic period (1820-1920), ending a piece with a minor chord had become more acceptable.

Due to harmonic developments in the 20th century, including both jazz and atonal classical music, the old distinction between consonant and dissonant intervals has largely evaporated. The only intervals that are still felt as dissonant by most listeners are the minor 2nd, the minor 9th, and, to a lesser extent, the major 2nd. The tritone, which was so disturbing to Renaissance musicians that they called it diabolus in musica (the Devil in music) is a consonant interval in jazz: Many jazz songs use a dominant 7th chord, which includes the tritone as the 3rd and 7th of the chord, as the tonic. And the major 7th is the characteristic interval in a major 7th chord, which is used as the tonic in just about all sweet-sounding jazz ballads. (For a full explanation of the intervals in these chords, see Chapter Five.)

In general, musical dissonances resolve into consonances. That is, one or more of the voices in a dissonant chord moves upward or downward, usually by a whole-step or half-step, to create a new chord that is consonant. The dissonant chord adds tension to the music, and the resolution of the dissonance into a consonance provides a release of the tension. It's not the case that all chord-based music includes dissonances, or that all dissonances resolve into consonances, but the resolution of dissonance into consonance is certainly central to the language of harmony.

Since we haven't yet explained what makes a chord dissonant, providing an example at this stage is difficult - but not impossible. Figure 2-12, which you may recognize, shows a dissonant interval (a major 2nd) resolving to a consonant interval (a minor 3rd). The resolution is produced by moving one of the notes of the dissonant interval down by a half-step.

Figure 2-12. The dissonant interval in bar 1 (a major 2nd) resolves to a consonant interval (a minor 3rd) in bar 2.

HOW TO HEAR INTERVALS

Learning to discriminate between the sounds of intervals takes practice. Fortunately, there are some mnemonic aids that will make it a little easier.

First, if you're hearing an interval in which both notes are being sounded at the same time, you may find it helpful to mentally break it up into a melodic interval. Imagine that you're hearing the lower note first, followed by the upper note. While practicing this technique, you may want to sing the two notes out loud. Listen to make sure your first note matches the lower note of the interval, and that your second note matches the upper note. Try singing the two notes in the other order, with the upper note first. Be careful not to transpose either of the notes up or down an octave, as this would invert the interval. Depending on your vocal range and where the interval is played, you might have to transpose them both up or down. If so, be careful to transpose them both by the same number of octaves.

To figure out what interval you're hearing, you may also find it useful to refer mentally to well-known melodies from pop and classical music. Due to copyright restrictions, it's not possible for us to publish even short excerpts from certain of the tunes listed on the next page. If you can't find them in sheet music form, doubtless a musically knowledgeable friend will be able to play any of the melodies that you don't already know, so that you can hear and become familiar with the intervals. Some of the tunes listed are in the public domain, which means we could publish them here, but a sketchy set of examples in which some of the more useful melodies are omitted would look pretty silly.