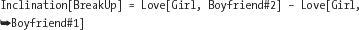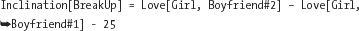Chris Crawford on Interactive Storytelling (25 page)

Least loyalty

No loyalty

Clearly, this list constitutes a verbal description of varying degrees of loyalty. Hence, you could easily assign numbers to it:

You could readily extend this list by adding more terms:

You could extend this list and achieve better precision if you didn’t stumble over imprecise—and, therefore, overlapping—terms such as “insignificant,” “strong,” and “great.” But these are limitations of the vocabulary; how do you know they’re intrinsic to the idea of loyalty? I agree that specifying somebody’s loyalty as 2,364,198.7349 is ridiculous; you couldn’t possibly insist that 2,364,198.7349 is correct and 2,364,198.7348 is wrong. Perhaps specifying loyalty with an integer scale of 0 to 100 is too ambitious; perhaps you should specify it on an integer scale of 0 to 10. The
principle
of quantification is not at issue—only the degree of precision is debatable.

Quantification is not dehumanizing, nor does it trivialize the complexity of the human condition. Finding the right value for a variable is analogous to finding the right word for a sentence. It’s just a matter of zeroing in on the precise content you want. The only difference is that the process is numerical rather than verbal. Quantification uses a different vocabulary, but it says the same things. The benefit is that this vocabulary can be used with a computer.

Despite all these arguments, some readers will still choke at the notion of quantifying human qualities. If all my reasoning fails to move you, is it perhaps because of a profound emotional aversion to all things mathematical? If so, I ask you to confront your feelings and determine whether you can set them aside in pursuit of the grand and glorious goal of realizing interactive storytelling. If you cannot, then this field of endeavor is not for you; you will always be unhappy struggling without the proper tools. Go, follow your muse elsewhere.

Now explore the palette of mathematical colors available to the artist. What do you have to work with?

The four fundamental arithmetic operators (addition, subtraction, multiplication, and division) provide the starting point. The easiest way to understand
them is as extensions of logical operations you’re already acquainted with. Start with addition. When you add two variables together, the sum will be large if the first number is large
or
the second number is large. Another way to think of it is to imagine the sum as a criterion for action. It sits inside a formula like this:

Heroism = Courage + Selflessness


IF (Heroism > 50) THEN


    DoTheRightThing


ELSE


    SitThereSniveling


In this case, the Actor in question will pass the test if EITHER his
Courage
OR his
Selflessness
is high. High
Courage
can compensate for low
Selflessness
, and vice versa.

Subtraction is really just addition backward; many situations that require subtraction could be handled by inverting the meaning on one term and using addition, as in this example:

Heroism = Courage - Selfishness


IF (Heroism > 50) THEN


    DoTheRightThing


ELSE


    SitThereSniveling


If you have set up a personality model to record Selfishness instead of Selflessness, you would use subtraction here. If you think about it, almost any kind of variable can be presented in a left-handed version and a right-handed version. Here are some examples:

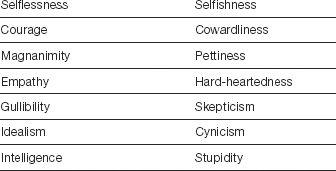
And so on. In some situations, you need to use subtraction instead of addition, but from a larger viewpoint, the two variables are just mirror images of each other.

The use of multiplication is just a bit more difficult to understand. Multiplication operates like an extension of the logical AND operator; you multiply two numbers together when BOTH the first number AND the second number are crucial to the outcome. For example, suppose an Actor has just been wronged by another Actor and is contemplating taking revenge. Suppose further that the two relevant variables in this case are Anger and Malevolence. The Actor’s inclination to take revenge is the product, not the sum, of his Anger and Malevolence because they don’t compensate for each other. All the anger in the world doesn’t cause a fundamentally benevolent person to seek revenge, and all the malevolence in the world doesn’t cause a happy person to seek revenge. That’s why multiplication, not addition, is called for in this case.

As with subtraction, division is just multiplication backward. In cases in which you would multiply by
Selflessness
, you would divide by
Selfishness
. However, division can blow up in your face. This happens when you divide by a value that turns out to be zero. This situation is bad; no computer in the world can handle division by zero, so your algorithm is bound to fail. You need to refrain from using division unless you are absolutely certain the denominator can never be zero. Sometimes you can guarantee this by simply adding a small constant to the denominator, like so:

Courage / (Selflessness + 5)


You might ask why I chose the value 5. That brings me to a whole new subject: weighting factors.

Rare is the case when the values of variables can be used directly; most of the time you must adjust them so that one variable plays a more important role. This adjustment requires the use of
weighting factors
.

The simplest kind of weighting factor is the additive weighting factor. For example, suppose that a female Actor must choose between two men, one of whom she already has a relationship with. Her inclination to leave Boyfriend #1 for Boyfriend #2 would be based on the difference in the degree to which she loves each:

For example, if the girl feels 46 Love for Boyfriend#1 and 52 Love for Boyfriend#2, the formula becomes:

Inclination[BreakUp] = 52 – 46


This formula yields a +6 Inclination to break up. Tough luck, Boyfriend#1!

But this formula has a flaw: We all have a natural resistance to change and tend to stick with what we already have. So the equation should be altered by making it a little harder to break up. You could accomplish this with the following change: