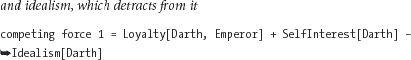Chris Crawford on Interactive Storytelling (23 page)

Having established the basic principle that mathematical formulas are simply a kind of syllogism, you can then make those formulas more complex. For example, a more accurate formula for a man’s weight might be something like this:

   All men’s weight is equal to 3 times their waist measurement plus their height.


Or to put it in the spare terminology of mathematics:

   Weight = 3 × Waist + Height


This equation is a little more accurate. It’s still not really true, but only in the absolute sense of getting exactly the right number for every man. This equation might get within 20 pounds of correctly predicting the weight of 70 percent of all men. That’s pretty good. You could probably make it better if you made the formula even more complex:

   Weight = 2 × Waist
1.5
+ 0.75 × Height – 12.1 × ShoeSize


Perhaps this equation would get within 10 pounds of correctly predicting the weight of 80 percent of all men. The perfect equation—the one that correctly predicts with zero error the weight of all men—is impossible to figure out. Perhaps it could be found with enough effort, but it would probably involve thousands of variables put together in the most intricate fashion and be dozens of pages long. For all practical purposes, perfection is impossible.

Perfection is seldom necessary, however. A chair designer needs to know the approximate relationship between the size and the weight of most people, but there’s no need for exact numbers; getting within 20 pounds is good enough. An interactive storyteller need not achieve perfection of mathematical description; getting close enough for dramatic fidelity is all that’s required.

One of the oldest figurative metaphors is Homer’s “rosy-fingered dawn.” It’s a powerful metaphor because it compares the rays of predawn sunlight and the fingers of the hand, suggesting an animation of a natural process. Poets are in the business of creating metaphors. So are most other artists, in at least some sense. The same thing applies to the mathematical modeling required for interactive storytelling. Indeed, this mathematical modeling is the essence of its artistic content—NOT the images, NOT the sounds, NOT the dialogue, NOT even the plot development. Sure, you can have artistic images in an interactive storytelling product, and you can stuff in a symphony or two, mix in a dash of poetry, and so forth, but that’s not interactive storytelling. You could create a movie consisting of little more than pictures of great paintings, but would it be a good movie? You could create a movie of a great poet reading poems, but would it be a good movie? You could create a movie showing an orchestra playing a Beethoven symphony, but would it be a good movie? Taking good art in one medium and simply transferring it to another medium doesn’t make the end result good art. Indeed, a true artist strives to express content most parallel to the grain of the medium.

This point is immensely important, but sadly, one that many people find difficult to accept. Part of their resistance arises from the passionate attachment that any artist feels for his or her art and its medium. Moviemakers love the cinema; poets adore poetry; writers worship literature. My claim that these magnificent art forms have no primary place in interactive storytelling sounds like a principal
telling a parent that her child isn’t good enough to attend his school. The same outraged rejection is the inevitable reaction to my claim.

But, hold, friend. I write these words not to belittle your child but to help you find the ideal place for your efforts. In past times, sons were forced to take up their father’s trade regardless of their own proclivities. This interactive storytelling medium might not be the best place for your talents or inclinations; if so, don’t fight it. Follow your muse.

And don’t try to prostitute your muse into a role for which she’s ill suited. In the earliest years of cinema, some gifted thespians attempted to force Melponene and Thalia into this new and alien medium. They simply set up the camera in the middle of the audience seating and acted out a play on the stage. These travesties earned the approbation of the better people, but nobody actually enjoyed them; they were inferior versions of the real thing. They were seen as rather like canned fruit: a feeble substitute for the real thing, but adequate for distribution to remote areas lacking access to the genuine article. They were also financial flops, buried by the success of vulgar, sensationalist collections of what were nothing more than carnival sideshows. As a consequence, thespians came to disdain the cinema as a simian medium. It took D.W. Griffith, a failed actor with no emotional attachments to the theater, to approach the cinema without preconceptions. No worshipper of Melponene and Thalia, he conjured up his own muse and succeeded where so many talented thespians had failed.

Therefore, friend, if you have already set your path on the well-trod way up the mountain peaks of other media, I wish you well but urge you not to drag the medium of interactive storytelling along with you. That is another mountain peak, along a very different path. Worse, the path to that mountain peak is unexplored and unmarked; you’ll need a machete as much as good hiking boots. Progress up this path will be slower than what you can accomplish in other media. You’ll not get there faster by taking the easier path.

If you can jettison your emotional attachments to other media (including games!) and approach interactive storytelling with the naiveté of a child, then you can accomplish something. If you try to force it to fit into your preconceptions, you will fail.

These things said, I shall now explain how to create metaphors using mathematical modeling.

I’ll start with a simple example: that overwrought moment in
The Return of the Jedi
when Darth Vader, watching the evil Emperor torture his son, Luke Skywalker, suddenly changes his mind, sides with Luke, and tosses the Emperor down a convenient deep shaft. As the Emperor blasts Luke with his nasty Evil-Electricity bolts, Darth looks at Luke, then at the Emperor, then at Luke, then at the Emperor—this goes on for what seems an eternity. Obviously, he is making a decision. In the film, the decision (and the difficulty of making it) is communicated through the long back-and-forth sequence. But in interactive storytelling, you must determine
how
this decision is made. What forces are at work in Darth’s mind?

Obviously, this decision represents a battle between two competing forces: his loyalty to the Emperor and his natural love for his son. But there are secondary forces as well: self-interest, which adds to his loyalty to the Emperor, and idealism, which detracts from it. There’s also the empathy that any person feels for those who suffer. These various factors do battle in Darth Vader’s mind to decide whether Darth should turn against the Emperor.

You can translate the ideas in the preceding paragraph into mathematical terms, line by line, sentence by sentence:

this decision represents a battle between two competing forces

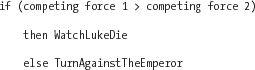
      IF (competing force 1 > competing force 2)


This formula is the mathematical representation of a simple yes-or-no decision. It doesn’t specify what happens in each of the two conditions; it merely establishes the decision’s basic form. If the strength of competing force 1 is greater than the strength of competing force 2, then the result is “yes.” We’ll figure out what “yes” means later.

his loyalty to the Emperor

      Competing force 1 = Loyalty[Darth, Emperor]


This formula simply represents the idea of loyalty with a mathematical variable that’s read as “Loyalty of Darth for the Emperor.” You specify the two Actors,
Darth and Emperor, because you could just as well worry about Loyalty of Darth for Luke or any other pairing of Actors.

Here’s the next term from my descriptive paragraph:

his natural love for his son

      competing force 2 = Love[Darth, Luke]


But there are secondary forces as well

This means you have to adjust the earlier formulas with additional factors, such as:

self-interest, which adds to his loyalty to the Emperor


competing force 1 = Loyalty[Darth, Emperor] + SelfInterest[Darth]

This new term is read as “Self-Interest of Darth” because it refers to Darth’s own self-interest. Again, you might want to use Luke’s Self-Interest somewhere else, so you might as well maintain the variable separately for each Actor.

This formula subtracts (“detracts”) Darth’s Idealism from his Loyalty to the Emperor. Onward:

There’s also the empathy that any person feels for those who suffer

competing force 2 = Love[Darth, Luke] + Empathy[Darth]


Next:

These various factors do battle in Darth Vader’s mind to decide whether Darth should turn against the Emperor.

Here
WatchLukeDie
is the verb for doing nothing, and
TurnAgainstTheEmperor
is the verb that leads to Darth shot-putting the Emperor.

Now assemble the whole thing in one fragment of pseudocode (
pseudocode
is a programmer’s term for code that’s not written in any particular programming language, but is so plain and simple in structure that anyone who knows how to program could understand it):

This little snippet might look like a gross simplification of human behavior, and indeed it is. It’s not about human behavior, but about drama. It is an artistic simplification. One of the most important realizations in mathematical modeling is that there’s no such thing as the “correct” model, only models that emphasize different facets of reality with more or less resolution and accuracy. The trick is to let go of a narrow-minded insistence on “correctness”; embrace the realization that the more you learn, the less you know; and regard reality with the playful attitude that every thought in your mind is merely a puppet-like rendition of the infinite complexity of reality. Humbly accept your work as sketches, not photographs. Don’t bemoan your failure to achieve photographic perfection in your paintings—revel in the cleanness of line, the clarity of image you can produce.