Gödel, Escher, Bach: An Eternal Golden Braid (27 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

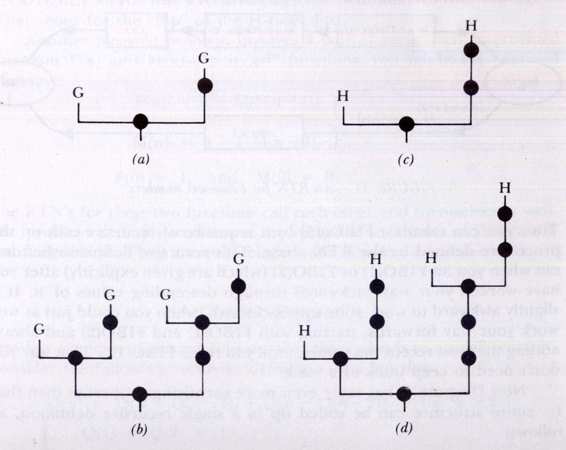
Diagram G and Recursive Sequences
Infinite geometrical structures can be defined in just this way-that is by expanding node after node. For example, let us define an infinite diagram called "Diagram G". To do so, we shall use an implicit representation. In two nodes, we shall write merely the letter `G', which, however, will stand for an entire copy of Diagram G. In Figure 29a, Diagram G is portrayed implicitly. Now if we wish to see Diagram G more explicitly, we expand each of the two G's-that is, we
replace them by the same diagram
, only reduced in scale (see Fig. 29b). This "second-order" version of Diagram gives us an inkling of what the final, impossible-to-realize Diagram G really looks like. In Figure 30 is shown a larger portion of Diagram G, where all the nodes have been numbered from the bottom up, and from left to right. Two extra nodes-numbers -- 1 and 2--- have been inserted at the bottom
This infinite tree has some very curious mathematical properties Running up its right-hand edge is the famous sequence of
Fibonacci numbers
.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, discovered around the year 1202 by Leonardo of Pisa, son of Bonaccio, ergo "Filius Bonacci", or "Fibonacci" for short. These numbers are best FIGURE 29. (a) Diagram G, unexpanded.
(c) Diagram H, unexpanded
(b) Diagram G, expanded once.
(d) Diagram H, expanded once
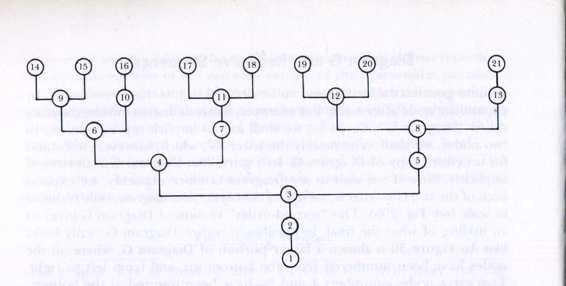
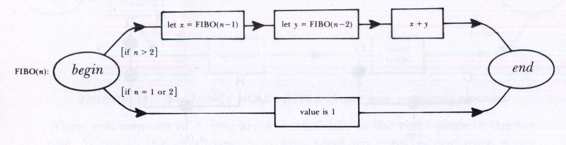
FIGURE 30. Diagram G, further expanded and with numbered nodes.
defined recursively by the pair of formulas
FIBO
(n) =
FIBO
(n- 1) +
FIBO
(n-2)
for n > 2
FIBO
(l) =
FIBO
(2) = 1
Notice how new Fibonacci numbers are defined in terms of previous Fibonacci numbers.
We could represent this pair of formulas in an
RTN
(see Fig. 31).
FIGURE 31. An
RTN
for Fibonacci numbers.
Thus you can calculate
FIBO
(15) by a sequence of recursive calls on the procedure defined by the
RTN
above. This recursive definition bottoms out when you hit
FIBO
(1) or
FIBO
(2) (which are given explicitly) after you have worked your way backwards through descending values of n. It is slightly awkward to work your way backwards, when you could just as well work your way forwards, starting with
FIBO
(l) and
FIBO
(2) and always adding the most recent two values, until you reach
FIBO
(15). That way you don't need to keep track of a stack.
Now Diagram G has some even more surprising properties than this. Its entire structure can be coded up in a single recursive definition, as follows:
G
(n) = n -
G
(
G
(n- 1)) for n > 0
G
(O) = 0
How does this function
G
(n) code for the tree-structure? Quite simply you construct a tree by placing
G
(n) below n, for all values of n, you recreate Diagram
G
. In fact, that is how I discovered Diagram
G
in the place. I was investigating the
function
G
, and in trying to calculate its values quickly, I conceived of displaying the values I already knew in a tree. T surprise, the tree turned out to have this extremely orderly recursive geometrical description.
What is more wonderful is that if you make the analogous tree function H(n) defined with one more nesting than
G—
H
(n) = n -
H(H(H
(n - 1)))
for n > 0
H
(0) = 0
--then the associated "Diagram
H
" is defined implicitly as shown in Figure 29c. The right-hand trunk contains one more node; that is the difference. The first recursive expansion of Diagram
H
is shown in Figure 29d. And so it goes, for any degree of nesting. There is a beautiful regularity to the recursive geometrical structures, which corresponds precisely to the recursive algebraic definitions.
A problem for curious readers is: suppose you flip Diagram
G
around as if in a mirror, and label the nodes of the new tree so they increase left to right. Can you find a recursive
algebraic
definition for this "flip-tree. What about for the "flip" of the
H
-tree?
Etc.?
Another pleasing problem involves a pair of recursively intertwined functions
F
(n) and
M
(n) -- "married" functions, you might say -- defined this way:
F
(n) = n -
M
(
F
(n- 1))
For
n
> 0
M(n) = n -
F
(
M
(n- 1))
F
(0) = 1, and
M
(0) = 0
The
RTN
's for these two functions call each other and themselves as well. The problem is simply to discover the recursive structures of Diagram
F
; and Diagram
M
.
They are quite elegant and simple.
A Chaotic Sequence
One last example of recursion in number theory leads to a small my Consider the following recursive definition of a function:
Q
(n) =
Q
(n -
Q
(n- 1)) +
Q
(n -
Q
(n-2)) for n > 2
Q
(1) =
Q
(2) = 1.
It is reminiscent of the Fibonacci definition in that each new value is a sum of two previous values-but not of the
immediately
previous two values. Instead, the two immediately previous values tell how far to count back to obtain the numbers to be added to make the new value! The first 17
Q
-numbers run as follows: 1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 6, 8, 8, 8, 10, 9, 10, . . . .
.. . 5 + 6 = 11 how far to move to the left New term
To obtain the next one, move leftwards (from the three dots) respectively 10 and 9 terms; you will hit a 5 and a 6, shown by the arrows. Their sum-1 l-yields the new value:
Q(
18).
This is the strange process by which the list of known
Q
-numbers is used to extend itself.
The resulting sequence is, to put it mildly, erratic. The further out you go, the less sense it seems to make. This is one of those very peculiar cases where what seems to be a somewhat natural definition leads to extremely puzzling behavior: chaos produced in a very orderly manner. One is naturally led to wonder whether the apparent chaos conceals some subtle regularity. Of course, by definition, there is regularity, but what is of interest is whether there is another way of characterizing this sequence-and with luck, a nonrecursive way.
Two Striking Recursive Graphs
The marvels of recursion in mathematics are innumerable, and it is not my purpose to present them all. However, there are a couple of particularly striking examples from my own experience which I feel are worth presenting. They are both graphs. One came up in the course of some number-theoretical investigations. The other came up in the course of my Ph.D. thesis work, in solid state physics. What is truly fascinating is that the graphs are closely related.
The first one (Fig. 32) is a graph of a function which I call
INT
(x). It is plotted here for x between 0 and 1. For x between any other pair of integers n and n + 1, you just find
INT
(x-n), then add n back. The structure of the plot is quite jumpy, as you can see. It consists of an infinite number of curved pieces, which get smaller and smaller towards the corners-and incidentally, less and less curved. Now if you look closely at each such piece, you will find that it is actually a copy of the full graph, merely curved! The implications are wild. One of them is that the graph of
INT
consists of nothing but copies of itself, nested down infinitely deeply. If you pick up any piece of the graph, no matter how small, you are holding a complete copy of the whole graph-in fact, infinitely many copies of it!
The fact that INT consists of nothing but copies of itself might make you think it is too ephemeral to exist. Its definition sounds too circular.
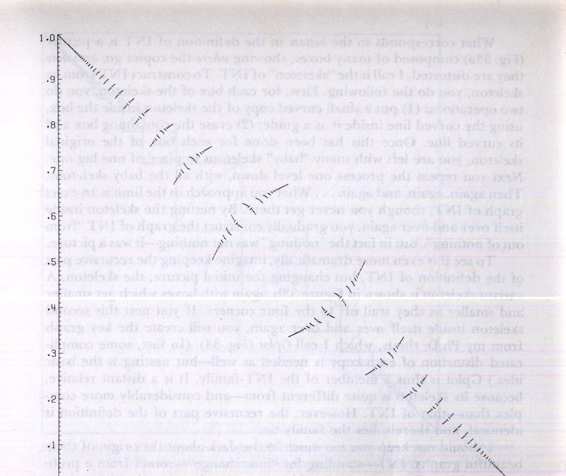
FIGURE 32. Graph of the function INT(x). There is a jump discontinuity at every rat
value of x.
How does it ever get off the ground? That is a very interesting matter. main thing to notice is that, to describe INT to someone who hasn't see it will not suffice merely to say,
"It consists of copies of itself." The o half of the story-the nonrecursive half-tells
where
those copies lie in the square, and
how
they have been deformed, relative to the full graph. Only the combination of these two aspects of INT will specify structure of INT. It is exactly as in the definition of Fibonacci number where you need two lines-one to define the
recursion
, the other to de the
bottom
(i.e., the values at the beginning). To be very concrete, if make one of the bottom values 3 instead of 1, you will produce a completely different sequence, known as the Lucas sequence:
1, 3, 4 , 7, 11, 18, 29, 47, 76, 123, .. .
the "bottom"
29 + 47 = 76
same recursive rule
as for the Fibonacci numbers
What corresponds to the
bottom
in the definition of INT is a picture (Fig. 33a) composed of many boxes, showing
where
the copies go, and
how
they are distorted. I call it the "skeleton" of
INT
. To construct
INT
from its skeleton, you do the following. First, for each box of the skeleton, you do two operations: (1) put a small curved copy of the skeleton inside the box, using the curved line inside it as a guide; (2) erase the containing box and its curved line. Once this has been done for each box of the original skeleton, you are left with many "baby" skeletons in place of one big one. Next you repeat the process one level down, with all the baby skeletons. Then again, again, and again ... What you approach in the limit is an exact graph of
INT
, though you never get there. By nesting the skeleton inside itself over and over again, you gradually construct the graph of
INT
"from out of nothing". But in fact the "nothing" was not nothing-it was a picture.
