Harnessed: How Language and Music Mimicked Nature and Transformed Ape to Man (28 page)

Another characteristic difference between rising and falling Doppler pitches from movers is that when a mover passes by, going straight, the pitch doesn’t just fall slowly with “inertia,” but
continues
to fall over an
extended portion
of the pitch range. The train that has reached your position has, for example, dropped from its maximum pitch to its baseline pitch, and will then drop through the lower half of the pitch range as it goes past and away. These kinds of long Doppler pitch runs, then, are more commonly downward than upward for movers in the physical world. Are long pitch runs for
melodies
more commonly downward than upward? Sean Barnett measured runs among the 10,000 classical themes. In particular, he recorded runs spanning the bottom or top half of the theme’s tessitura. Setting a low bar for what counts as a run—two or more notes approximately filling (more than 80 percent) the upper or lower half of the tessitura—51.86 percent of the 212,542 runs were downward. A two-note run is not very runlike, and our expectation is that if we create a more stringent standard for what counts as a run, then we should find an even greater asymmetry between up and down, with an even greater share of runs being down. Indeed, when Sean required a run to have five or more notes in the same direction, 54.22 percent of the 11,119 runs that qualified were in the downward direction.

Consider now yet another ecological regularity in this vein. Let’s ask ourselves: are these falling-pitch runs due to straight-moving movers more likely to occur when movers are near or far? When a mover is far away, in order for that mover to implement a long downward run, the mover must continue straight for a great many steps without turning. It is quite likely that the mover will turn somewhere over the course of that long walk. But if the mover is close by, the mover need only move straight for a relatively small number of steps to engender a substantial downward pitch run. Big downward Doppler pitch runs are therefore disproportionately probable when near. Do we find this in music? As we discussed in Chapter 4, distance from the listener is encoded in music by loudness, and so our expectation here is that louder segments of music (i.e., passages depicting a more proximal mover) are more likely to have good-sized downward pitch runs. RPI graduate student Romann Weber measured runs spanning at least half the tessitura from Denes Agay’s
The Classical Period
, and calculated the probability that such pitch runs are downward as a function of loudness. As can be seen in Figure 50, the probability of a large downward pitch run rises with loudness, consistent with the ecological expectation.

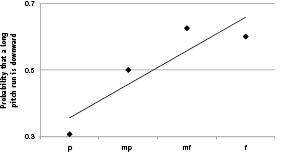
Figure 50
. Pitch runs spanning at least half the tessitura width among a sample of 37 pieces from Denes Agay’s
An Anthology of Piano Music, Vol. II: The Classical Period
. Forty such runs were found, the loudness during the run measured, and the relative probability that the run is up or down computed. Louder segments of music have a greater probability of long downward runs, consistent with expectations from human movement.

Newton’s First Law is found in music where it should be found if melodic pitch is about Doppler shifts. Melodic pitch acts like a mover’s direction, and thus has
no
pitch momentum, just as inertia predicts. But as we looked more closely, we realized that there are fundamental asymmetries between upward and downward Doppler pitch changes, asymmetries also found in melody. Melody does show pitch momentum in the special case of small downward changes in pitch, as expected from the dynamics of movers. And melody generally drifts downward gradually, as expected from the fact that all straight-moving movers have slowly falling pitch (unless moving directly toward or away from the listener). And melody takes larger jumps upward than downward in pitch, also something expected from movers orienting their bouts of behavior toward you. Melody also favors longer runs downward than upward, something we also expected from the sounds of movers. And finally, like closer movers, louder segments of music tend to have disproportionately more large downward pitch runs.

The Encore sections thus far have mostly concerned rhythm and melody. Loudness did come up in Encores 4, 6, and 7. The next and last Encore section is about loudness, providing further evidence that loudness in music behaves like loudness due to the proximity of the mover.

8
Medium Encounters

In the Chapter 4 section titled “Slow Loudness, Fast Pitch,” we saw that loudness varies slowly, consistent with the time scales required for movers to vary their distance from you, the listener. We must be more careful, though. If a mover were a “close talker,” tending to move about uncomfortably close to you, then even small changes in distance could lead to large changes in loudness, due to the inverse square law for loudness and distance. But in real life, more than close encounters, we tend to have medium encounters: the movers we typically listen to tend to be in the several- to ten-meter range, not in the centimeter range, and not in the tens or hundreds of meters range. At “medium” distances, large loudness modulations don’t occur over just one or several steps. They require more steps, plausibly in the range of the approximately 10 beats we found for the average loudness duration in Chapter 4.

Not only are our experiences of movers usually at a “medium” distance, but it seems reasonable to expect that individual bouts of behavior tend to occur at an average “medium” distance. Recall our generic encounters from the section titled “Musical Encounters” in Chapter 4: the “center of mass” of the A-B-C-D cycle of movement would be representative of the average distance of a generic encounter. We see, then, that loudnesses of movers will tend to have a
typical
value. We therefore expect any piece of music to have a baseline loudness level it spends a disproportionate amount of time at, spending less time at loudness levels farther away from this average. Unlike Doppler pitches, which have a distribution that is fairly broad and flat, the distribution of mover loudnesses tends to be more peaked. Is music like this? Does music spend most of its time at an average loudness level, relatively rarely venture out of that loudness zone, and more rarely still pursue greater loudness deviations from the average? Music is
indeed
roughly like this. Music tends to use
mezzo forte
as this baseline, with lesser and greater loudness levels happening progressively more rarely. RPI students Caitlin Morris and Eric Jordan measured the average percentage of a song spent at each of its loudness levels, and the results are shown in Figure 51. One can see that there is a strong “mountain” shape to the plot: pieces tend to spend more time at intermediate loudness levels than at loudness levels deviating far from the central values. (Although our data were broadly consistent with our expectation, there was a slight downward divot at
mezzo forte
relative to
piano
and
forte
, with the greatest percentage of time spent in
piano
.)

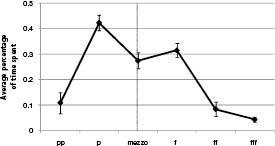
Figure 51
. For each song, the total percentage of time spent at each loudness level was determined. These distributions were then averaged together across 43 pieces in Denes Agay’s
An Anthology of Piano Music, Vol. II: The Classical Period
.

We can say more. Consider the obvious fact that there is less real estate—less space—near you than far from you. This asymmetry means that a mover has more chances to be farther than average from you than to be nearer than average to you. There should not only be, then, a roughly mountain shape to Figure 51, but the below-average levels of loudness should be more common than the above-average levels of loudness. The mountain should have a higher level at lower-than-average levels of loudness. The distribution we just plotted in Figure 51
has
, in fact, this expected asymmetry.

We can say something further still. Not only should movers spend a greater proportion of their time relatively far away than relatively nearby, but when they
do
get near, and thus relatively loud, this should be more transient. Why? Because the mover will more quickly leave the near region, for the simple reason that “the near” is an inherently smaller piece of land than “the far.” This is indeed the case, as shown in Figure 52, also obtained by Caitlin Morris and Eric Jordan

Figure 52
. For each song, the average duration of each loudness level was computed, and then these per-song average normalized so that the sum across the levels equaled one. Then, these were averaged across 43 pieces measured in Denes Agay’s
An Anthology of Piano Music, Vol. II: The Classical Period
. One can see the asymmetry. As predicted from the spatial asymmetries of near and far, music should tend to have longer durations at lower-than-average loudness levels compared to higher-than-average loudness levels.

We see, then, that loudnesses distribute themselves as expected if they are about proximity. Encounters have a typical distance; more cumulative time is spent farther than nearer; and nearer segments of encounters tend to be short-lived relative to farther segments.

Appendix

Word Events

Language data

Data about word structure was acquired from 18 languages: [Indo-European] (1) English, (2) German, (3) Spanish, (4) Bengali, (5) Bosnian; [Altaic] (6) Turkish; [American] (7) Inukitut, (8) Taino, (9) Yucatec Maya; (African) (10) Lango, (11) Somali, (12) Wolof, (13) Zulu, (14) Haya; [Austronesian] (15) Fijian, (16) Malagasy; [Dravidian] (17) Tamil; [East Asian] (18) Japanese. In each case we acquired a sample of common words (an average of 937 (sterr = 134) words per language); our analysis confined itself to those words having three or fewer non-sonorants (an average of 775 (sterr = 103) words per language). In many cases, data were obtained from transliterated dictionaries, and the phonological interpretation of the transliteration (for which we cared only about whether phonemes were plosives, fricatives or sonorants) obtained from a variety of sources (some included in Table 1). Each word in the sample was measured by converting each plosive to a ‘b’, each fricative to an ‘s’, and any adjacent sequence of sonorants to an ‘a’. Sonorants included vowels, as well as sonorant consonants (like y, w, l, r, m, n, and ng). Also, words beginning with a vowel typically begin with a glottal consonant, which was treated as a plosive, and coded as starting with a ‘b’ before the ‘a’ of the vowel. Affricates (like “ch” and “j”) were coded as ‘bs’. Table 2 shows the counts for each structure type within each sampled language. For words beginning with a sonorant, only those having two or fewer non-sonorants were included; this is because, as discussed in the main text, these sonorant-start words are predicted as cases where a ring was initiated with an inaudible hit. As a test of the methodology for determining word structure type from words, a naïve observer was asked to code the 863 words with three or fewer non-sonorants for our sample of German; when plotted against the frequency counts of the structure types as coded by the first author, the best-fit equation on a log-log plot was y = 0.95x
0.92
, or nearly the identity (
y
=
x
), with a correlation R
2
= 0.88.

Table 1
. Languages from which samples of word structure types were acquired. Citations are given to the word list, and to at least one source for phonological information used in categorizing orthographic elements as plosives, fricatives, or sonorants.

Video data

Our hypothesis is that it is the physical events among macroscopic solid objects that principally drives the competencies of our auditory system, and thus coders were trained to measure sequences of hits and slides in the physical events found in videos. To avoid any potential auditory bias to hear speech-like patterns among natural event sounds, measurements were made visually (i.e., with the video’s audio muted). Measurements were made from several categories of video, each chosen because of the likelihood of finding “typical” kinds of solid-object physical events. Categories were as shown below, followed by links to the videos (and their lengths).

• Cooking (23 minutes)
  
• http://www.youtube.com/watch?v=6s__hRrQZ3E
  (9:29)
  
• http://www.youtube.com/watch?v=Y36zINLldyQ
  (3:49)
  
• http://www.youtube.com/watch?v=Enytl9Epfcs&feature=related
  (9:50)
  
• Assembly instructions (17 minutes)
  
• http://www.youtube.com/watch?v=fOofJFyu9s8
  (1:37)
  
• http://www.youtube.com/watch?v=Y-oPmSCIQPw
  (0:48)
  
• http://www.youtube.com/watch?v=Z_8otugkqxM
  (2:31)
  
• http://www.youtube.com/watch?v=hsd7vne65nA
  (4:55)
  
• http://www.youtube.com/watch?v=Dd8Y5prcCos
  (7:39)
  
• Children playing with toys (7 minutes)
  
• http://www.youtube.com/watch?v=yRPoBXZcx_o
  (1:56)
  
• http://www.youtube.com/watch?v=_1-TbrU8W0M
  (1:17)
  
• http://www.youtube.com/watch?v=4gYMerbfYpM
  (1:10)
  
• http://www.youtube.com/watch?v=O28i03T82EE&NR=1
  (0:46)
  
• http://www.youtube.com/watch?v=BSbV4U62Mg0&feature=related
  (1:45)
  
• Acrobatics (8 minutes)
  
• http://www.youtube.com/watch?v=RKoKtHzrTEw
  (2:22)
  
• http://www.youtube.com/watch?v=KXpbCQ6kIVQ&feature=related
  (1:59)
  
• http://www.youtube.com/watch?v=VY9g7koP8yQ
  (3:41)
  
• Family gatherings (11 minutes)
  
• http://www.youtube.com/watch?v=H11dO6tr3v4
  (2:44)
  
• http://www.youtube.com/watch?v=m_q6QRD4hLU
  (8:17)
  

These amount to 67 minutes of video in total. The average (across the three viewers) total number of events with three or fewer physical interactions (i.e., hits or slides) among these videos was 504.7. The correlations between the relative frequency distributions for the three viewers were R2 = 0.51, R2 = 0.63, R2 = 0.48. These three coders also measured from the same videos a second time, this time with the sound present; the average distribution for vision only was highly correlated with the average distribution for audition-and-vision (R2 = 0.857). Also, as part of the training for coding, a “ground truth” auditory file was created by the first author with sample physical event types, and the two coders measured, via audition only, the distribution, and had correlations of R2 = 0.63 and R2 = 0.64 with the ground truth source.