Secrets of Antigravity Propulsion (25 page)

The lower trace in figure 6.9 depicts a typical shock current pulse detected by the reference antenna that is displayed as a positive voltage rise, its voltage maximum being indicated by an arrow.
The upper trace in figure 6.9 shows the corresponding superluminal surface wave shock pulse detected by the second monopole antenna pickup positioned 189.5 centimeters from the ground-current-sensing reference antenna.
Its first negative potential peak is also marked with an arrow, the surface wave’s polarity being the inverse of the detected ground plane current impulse.
The time interval between the two arrows indicates the time-of-flight of the superluminal surface wave.
The timing of a given marker was accurate to approximately 125 picoseconds.
The temporal width of the shock’s lead wave cycle varied very little as it moved outward, the wave cycle having a duration of about 1.77 ± 0.09 nanoseconds.
Figure 6.10 shows the time-of-flight of the pulses as measured at various distances from the dome electrode’s ground.
The measurements are marked as black circles and a suggested model fit is represented by the small black diamonds.
The 61-centimeter data point was given a zero time lapse since the oscilloscope measurements indicated that the pulse spanned this near-electrode distance virtually instantaneously.
Figure 6.11 shows the speed estimated for the shock at various distances from the impulse generator’s ground point based on the time-of-flight model fit performed in figure 6.10.
This shows that at 80 centimeters from the ground-current-sensing reference antenna, the shock had a superluminal speed of approximately 2.32 times the speed of light, its speed progressively dropping toward the rest frame light speed (
c
) with increasing travel distance.
The model shown assumes that ether velocity (
v
) varies with distance (d) as:
v
= kc/(d – 61)
1.1±0.1
, in which k equals 33.6 centimeters and a distance 61 centimeters from the ground reference point is chosen as the model’s zero point.
Superluminal velocity (
c
') is then given as:
c
' =
c + v
.
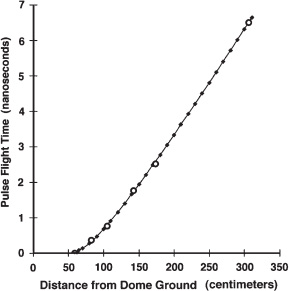
Figure 6.10.
Graph showing shock front pulse time-of-flight as a function of
distance from the emitting impulse generator ground.
Black circles indicate
actual data points.
Small black diamonds plot the best fit to these data points
based on the velocity-distance model plotted in figure 6.11.
(Data taken by
Obolensky and processed by LaViolette; © 2007, P.
LaViolette)
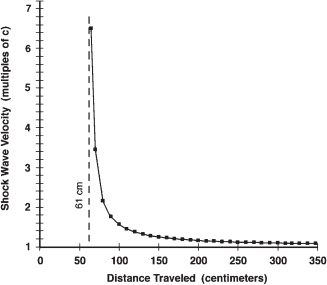
Figure 6.11.
Graph showing superluminal shock front velocity plotted as a function of distance from the emitting dome’s ground-current-sensing reference antenna.
Gray squares indicate the model that makes the best fit to the six time-of-flight data points plotted in figure 6.10.
With increasing travel distance, shock velocity declines toward c as subquantum kinetics predicts.
(Data taken by Obolensky and processed by LaViolette; © 2007, P.
LaViolette)
The data strongly support the subquantum kinetics prediction that the superluminal speed of such a wave should decrease with increasing distance when radiated from a magnifying transmitter dome.
Furthermore, they show that superluminal speed is a characteristic of shock discharges regardless of whether the discharges are emitted from a superconducting electrode of the sort used in the experiment by Podkletnov and Modanese.
Finally, these results lend support to the unpublished findings of Podkletnov and Modanese that their gravity wave impulse had traveled at a high superluminal speed.
In other words, taking the work of Tesla and that of Podkletnov and Modanese in context, we see that superluminal shock front propagation speeds are the norm rather than the exception.
Superluminal propagation speeds have also been observed in atomic bomb tests.
Scientists working for the military have known since the early bomb tests in the late 1940s that the electromagnetic pulse shock wave from a nuclear explosion propagates outward at superluminal velocities when measured near the explosion epicenter.
The enormous energy released in the explosion accelerates the fireball’s free electrons radially outward at a relativistic velocity, generating a radially propagating shock pulse that, like a shock discharge from Obolensky’s magnifying transmitter, moves outward at superluminal speeds.
Subquantum kinetics attributes this breaking of the “light barrier” to the creation of a tremendous radial ether wind generated by the electric gradient of the advancing shock.
For an isotropic explosion, the velocity of this ether wind would decline approximately as the inverse of the distance traveled, and similarly, the velocity of the electromagnetic pulse shock would be expected to follow this decline in an asymptotic approach to the velocity of light.
At such a time when the data are declassified, it would be worth checking to see if the subquantum kinetics velocity decline prediction was born out.
Clearly, the results of Obolensky’s magnifying transmitter experiment violate the fundamental premise of special relativity that energy cannot be transmitted faster than the speed of light.
Beyond 1 meter from the dome’s ground-current connection, the shock front travel distance exceeded the shock front’s wavelength.
Moreover, by the time the pulse had reached the 3-meter mark, its flight distance exceeded five pulse wavelengths.
Hence, the superluminal speeds observed cannot be explained away as an allowable violation arising from quantum entanglement of the photon quantum, nor can they be ascribed to a change in shape of the shock wave profile.
Thus, Einstein’s theory is certainly disproved and the subquantum kinetics ether theory is vindicated.
*19
6.3 • INTERSTELLAR SPACE TRAVEL
By itself, the electrogravitic impulse effect could serve as an excellent drive for use in interstellar space travel.
One could imagine a spacecraft outfitted with a large-aperture Podkletnov gravity beam projector that would be powered by a set of very high-power Marx capacitor banks operating at potentials of up to 2 million volts and conveying its discharge to a superconducting electrode seventy times larger in diameter than the superconducting disc Podkletnov fabricated for his beam generator, that is, 7 meters in diameter instead of 10 centimeters.
The beam generator would be mounted at the rear of the ship and would direct its gravity pulses forward toward the ship’s bow.
Suppose that, like Podkletnov’s laboratory apparatus, the ship’s gravity beam generator were to produce impulse accelerations of greater than 500,000 g over the brief 100-nanosecond pulse interval.
Also suppose that the ship’s capacitor banks have sufficient time to recharge to deliver these pulses once per second, a rate sixty times greater than Podkletnov’s apparatus was able to achieve.
Averaging this gravity impulse over the 1-second interval between successive pulses, we find that this would be the same as if the ship experienced a continuous acceleration of about 0.05 g, or 5 percent of the Earth’s accelerating force.
However, to run such a propulsion unit would require an enormous amount of power, 6,000 megawatts, which is 300,000 times more than the 20 kilowatts that Podkletnov and Modanese were using.
Such power could be supplied by a set of large-sized nuclear power plants, similar to those operated by some electric utilities.
Or it might be provided by an onboard “free energy” generator such as the gravity wave power generator described in the next section or by a Searl effect generator such as that described in chapter 10.
The beam would need to be designed to produce a very uniform acceleration across the surface of its electrode so as to minimize the development of gravitational sheer forces.
If the craft’s occupants were seated in the path of such a beam, they would feel no acceleration since every atom of their bodies, and the entire ship as well, would be uniformly accelerated by the gravitic pulses.
The aperture of the beam would need to be made slightly larger than the craft so as to avoid the rapid drop-off in the accelerating force at the periphery of the beam.
There would be no fear of meteor collisions because the beam’s forward-directed gravitic pulses would clear out a path ahead of the ship that would be free of interstellar debris.
By negatively charging the ship’s bow, a repulsive gravitic field could be built up there that could deflect any meteor that happened to make a last-minute entry into the ship’s flight path.
With an acceleration of 0.05 g, the journey to even the nearest star would take far too long to be practical for manned interstellar space flight.
Such an endeavor would require engines capable of delivering gravitational accelerating forces on the order of 10 g.
If the Podkletnov-Modanese beam generator was used, a pulse repetition rate two hundred times greater would be needed, or about one pulse every 5 milliseconds.
However, the power demand would rise to the enormous figure of 1,200 gigawatts, which is three times the average rate of power consumption of the United States or six times the thrust power produced by the first stage of a Saturn V rocket.
Let us for the moment overlook the practicality of generating such a large amount of power on board a spaceship.
Propelled by 10 g of acceleration, a ship would be able to accelerate to 2.8 percent of the speed of light in just one day.
By one week, it would be up to 20 percent of the speed of light, and after one month it would be traveling at about 85 percent of the speed of light.
Once up to this subthreshold light speed, having consumed three times the annual power consumption of the state of California, the crew could shut off the beam propulsion system and coast for the remainder of the journey.
The time to reach Alpha Centauri, the nearest star system, lying 4.37 light-years away, would be just five years and two months.
Upon nearing the Alpha Centauri system, the spacecraft would rotate itself 180 degrees and then would once again turn on its gravity propulsion beam to decelerate.
Navigation could easily be done by using the “galactic GPS system,” the network of pulsar beacons that is deployed throughout the galaxy.
(See my book
Decoding the Message of the Pulsars
for more about the use of pulsars for interstellar flight navigation.)
Gravity beam technology, in its current state of development, is impractical from the standpoint of energy efficiency.
A spacecraft having a mass of 700 tons, accelerated at 10 g with an energy consumption of 1,200 gigawatts, would have a thrust-to-power ratio of about 5 × 10
-3
newtons per kilowatt, or about fifty times less than that of the NASA Lewis Research Center ion engine.
Perhaps a hundredfold-higher efficiency might be secured if the craft’s superconducting discs were powered by improved Marx capacitor banks of the sort Podkletnov used in generating the 10-million-volt concrete-smashing pulses.
However, this would still not be much of an improvement over the efficiency of an ion engine.
If used alone, the gravity beam technology would be more practical if the beam generator and its power supply were to be located at a stationary spaceport facility with the beam being directed toward a specific destination to which one wished to travel.
The spaceship would then simply need to be navigated to keep it positioned within the beam.
One advantage of the gravity beam technology would be its ability to propel the ether forward to a very high velocity within the confines of its beam, thereby creating an ether-frame dragging effect that would allow a ship to approach or even exceed the speed of light without harmful consequences to its passengers.
As we have seen in the previous section, it is possible to transmit shock waves at superluminal speeds, presumably because of their ability to surf the forward-moving ether wind.
So, we may conclude that it should also be possible to accelerate a ship to superluminal speeds.
Unlike special relativity, subquantum kinetics allows the possibility that both matter and energy waves could be made to propagate at superluminal velocities.
The gravity beam would not only propel the ship forward, but it would also push forward the ether within its superluminal tunnel.
In standard physics terms, the gravity beam, in effect, would be accelerating the ship’s local rest frame to superluminal velocities.
As noted earlier, the Podkletnov gravity beam generator has been observed to produce gravity shocks that travel at enormous superluminal speeds.
Based on this, we may conclude that it is technically possible to accelerate a “beam ship” to similar speeds, allowing it to travel toward its destination at hundreds or even thousands of times the speed of light.
Perhaps interstellar space travel could be made practical if Brown’s electrokinetic thrusters, considered in chapter 3, were used in conjunction with the gravity impulse beam drive, thereby tremendously reducing the energy requirements.
The power requirements for a trip to Alpha Centauri might then be brought down to around 50 megawatts, comparable to the output of a nuclear submarine reactor.
The initial phase of acceleration would be accomplished mainly through the operation of the electrokinetic thrusters.
During this time, the gravity beam drive would be operated in a low power mode to conserve energy.
Its main purpose would be to propel the ether forward so that the ship would not be exposed to an opposing ether wind.
Then, after accelerating for several weeks up to a sublight speed of say 85 percent of the speed of light, the gravity impulse engine would be brought up to maximum impulse power, allowing the ship to accelerate through its ether wind tunnel to a superluminal speed of 200 c.
The remaining journey to the Alpha Centauri environs would then take only one week.
If there ever were a
Star Trek–style
impulse engine, this would be it, except instead of saying “Warp 5, Scotty,” the captain might say “Grad 5, Scotty,” consistent with the ether gradient concept of subquantum kinetics.
*20
For longer interstellar journeys, a spaceship might accelerate to speeds exceeding 3,000
c
, equivalent to Warp 11.
Then a journey to our nearest satellite galaxy, the Magellanic Cloud, which lies 180,000 light-years away, would take only sixty years.
Is superluminal space travel possible?
The answer is a resounding YES!
It is no longer science fiction.
It can be done using off-the-shelf technology coupled with a minimal amount of R&D.
Commit $500 million and one hundred engineers and technicians to the project, and an interstellar drive unit could be built within, say, ten years’ time.
