Simply Complexity (27 page)
Authors: Neil Johnson

This is where Mike Spagat and Jorge Restrepo enter the picture. Together with their collaborators in Bogota, Colombia – in particular, Oscar Becerra, Nicolas Suarez, Juan Camilo Bohorquez, Roberto Zarama and Elvira Maria Restrepo – they built and analyzed a huge, detailed dataset for the twenty-plus-year war in Colombia. Then they did the same for the war in Iraq, building on the database of the Iraq Body Count team. If they had wanted to, the researchers could have just added together all the casualties in each war, and then added these two datapoints – one for Colombia and one for Iraq – to Richardson’s curve in
figure 9.2
. However, they instead did something far more interesting and unique.
What Mike Spagat, Jorge Restrepo and the rest of the team did was to pursue the following line of thinking: wars follow a power-law, and wars are a human activity. But given that a war is generally made up of lots of smaller battles or clashes, like “wars within wars”,
would we also see a similar pattern emerging within a single war? In other words, can a single war be seen as a set of wars-within-wars?
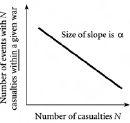
Figure 9.3
Wars within a war. Pattern of casualties from the events within a given war, such as Iraq or Colombia. The graph shows a log-log plot of the number of events with
N
casualties within a given war, against the number of casualties
N
.
This is exactly what they found. Despite the very different origins, motivations, locations and durations of the wars in Iraq and Colombia, they found similar power-law patterns in the casualty figures for the events within each war. This result is sketched in
figure 9.3
. Their finding is remarkable not only because of the different conditions of the wars, and their very different locations, but also their different durations. The Iraq war is basically being fought in deserts and cities and, at the time of writing, has only been going on for a few years. By contrast, the guerilla war in Colombia is mainly fought in mountainous jungle regions, and has been ongoing for more than twenty years against a fairly unique back-drop of drug-trafficking and Mafia activity.
What Mike and Jorge’s findings suggest is that the way in which such modern wars unfold as time goes by has less to do with geography or ideology and much more to do with the dayto-day mechanics of human insurgency – in other words, it has to do with the
way
in which groups of human beings fight each other. And this is
exactly
the same kind of common feature that we found in financial markets in
chapter 6
. Despite their very different locations, operating rules and ages, two markets can have very similar values of their fractal parameter
a
(which is analogous to the size of the power-law slope α in the present context). The reason? It is all down to human nature. When left to their own devices, without any “invisible hand” or central controller, human groups interact in such a way as to produce markets with similar characteristics, and wars with similar characteristics. This is because a collection of humans who are competing for some limited resource is an excellent example of a Complex System – and Complex Systems show certain levels of universality. And wars, like markets and traffic, are all just examples of Complex Systems.
They then took their analysis further, looking at how the war is evolving in time. In other words, they chopped up the length of the war since its beginning into little sections and found that the data in each piece also followed a power-law. They then deduced the slope of the power-law for each piece. Their result is sketched
in
figure 9.4
. Remarkably, the size of the power-law slope in each war has crept toward 2.5 which is exactly the same as the coefficient for global terrorism in non-G7 countries. This suggests that both these wars and global non-G7 terrorism currently show the same underlying patterns and hence character. This in turn suggests that the insurgent forces underlying these modern wars and terrorism, are now effectively identical in terms of how they are operating. You might think this is good news since resolving one of the conflicts could then give a clue about how to resolve the rest. On a more pessimistic note one could of course say that we won’t resolve any of them without resolving all the rest. In some sense, it is all part of one big ongoing war.

Figure 9.4
The future of wars? The two modern, but very different, wars in Iraq and Colombia seem to have evolved in such a way that they currently have the same form. And this form in turn matches the pattern of terrorist attacks in non-G7 countries.
But what is so special about an α value of 2.5? In other words, why does the value 2.5 emerge for things as supposedly unconnected as Iraq, Colombia and non-G7 terrorism? The answer lies in the human activity of forming groups.
The mathematical model developed by Mike Spagat and his team puts forward the idea that any modern insurgent force – whether in
Iraq, Colombia, or a terrorist organization – operates as a network of fairly self-contained units which evolve in time. They call these units “attack units”. Each attack unit has a particular “attack strength” which indicates the average number of casualties which will arise in an event in which this attack unit is involved. As the war unfolds in time, these attack units either join forces with other attack units or break up. In the real war, joining forces or breaking up would probably involve a decision process – hence one would ideally invoke a decision-making model similar to the bar-attendance and “which route?” problems of
chapter 4
. In other words, we have said that a war is a collection of people competing for limited resources – so a model of whether to choose option 1 (i.e. combine with another attack unit) or option 0 (i.e. break up) might make sense. However, such a combination of models would be difficult to analyze mathematically. Instead, Mike and Jorge found that they could use a much simpler description of insurgent decision-making, and yet still explain the observed data. In particular, the researchers assumed that the attack units effectively use a coin to make decisions about whether to combine or
break up. In particular, Mike and Jorge assumed that attack units join together with a given probability 1-
p
, and break apart with a probability
p
. They then allowed this process, whereby attack units break up or combine, to carry on indefinitely. To their surprise they found that the insurgent force reached a kind of status quo in which the distribution in the number of attack units with a given attack strength followed a power-law. Since each attack unit will produce an average number of casualties equal to its attack strength in any given event, this distribution also represents the distribution of the number of events with a given number of casualties. So this agrees nicely with the real casualty data – but the surprises don’t stop there. Remarkably, the value of the power-law slope which emerges from the model is 2.5, which is the same value of α as that obtained for the real wars and non-G7 terrorism in
figure 9.4
. This is an incredible finding.
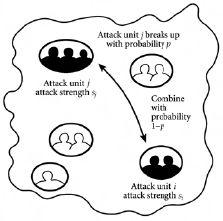
Figure 9.5
Breaking up and getting together: a model which reproduces the power-law pattern observed in the modern ongoing wars in Iraq, Colombia and global terrorism in non-G7 countries.
Why should a power-law arise from such a model? We already discussed how the real war is a Complex System – but what about the model? We saw in
chapter 3
that feedback is needed to produce a power-law – so where is that feedback coming from in Mike and Jorge’s model? It turns out that it arises as follows. The precise distribution of attack units that are available for breaking up or combining at a given moment in the war will depend on what has been happening to the soup of attack units leading up to this moment – and this, by definition, means that there is feedback from the past. As a result of this feedback the distribution of attack units, and hence casualties, will neither be completely disordered nor completely ordered. Instead, it gives us something which is complex in exactly the same way that the slightly sober drunkard’s walk in
chapter 3
was complex. That example gave us a complex walk which was neither completely disordered, like a true drunkard, nor completely ordered like a sober walker – it is a fractal. Here we have the equivalent – but in terms of group-formation, in a space containing insurgents.
The upshot of all this is that Mike and Jorge’s findings offer a novel “Complex Systems” interpretation of the evolution of modern wars and terrorism. In particular, their results in
figure 9.4
suggest that the Iraq war began as a conventional confrontation between large armies, but continuous pressure applied to the
Iraqis by coalition forces broke up the insurgency into a collection of attack units. In Colombia, on the other hand, the same end result has been arrived at in the opposite way. In particular, the guerrillas in the early 1990s were unable to join up into high-impact units – hence the attack units were all very small. But since then they have gradually been acquiring comparable capabilities, and now have a distribution of attack units which is as wide as that of the insurgents in Iraq. Furthermore, the fact that both Iraq and Colombia currently have the same power-law slope as non-G7 terrorism suggests that the attack unit structures in all three arenas are currently the same.
This is all quite remarkable. Nobody would disagree that wars are terrible human tragedies, charged with emotions and irrationality. And yet it looks like they can be interpreted – and even understood – using Complexity Science.
But all this rests on the quality of the data. So what if someone has artificially inflated or deflated the casualty numbers for Iraq or Colombia? After all, there is likely to be a great temptation to do so depending on which side is reporting the numbers. Well, it is a particular feature of Mike and Jorge’s work that their analysis tends to avoid such problems. It turns out that the slope of a power-law is insensitive to the total number of casualties. Any systematic multiplication of the raw numbers by some constant factor has no affect on the slope and hence the value of α. This is because a power-law looks at the
pattern
of events and hence casualties, as opposed to simply monitoring the aggregate number. For this reason, Mike and Jorge have done something which is far more subtle and insightful than merely tracking how the total number of casualties changes over the lifetime of any given war.
Let’s think about this for a moment. Imagine someone has given you the total number of casualties in two insurgent wars, and that these numbers are similar. It doesn’t actually tell you very much since these numbers might be explained by the fact that the countries involved were of a similar size, or by the fact that the insurgent armies involved had a similar total size. The far more important question is whether the
way
in which the two insurgent groups are waging war is similar. This is what one would like to detect – and this is precisely what the power-law
analysis of Mike Spagat and Jorge Restrepo has detected. In short, they have used a Complex Systems focus to uncover a common hidden character in modern wars – and that is something very significant. Furthermore, with the help of Ben Burnett and Alex Dixon, they are now extending their mathematical model to describe the co-existence of several different “species” of insurgent groups – in other words, a true ecology of conflict.
