The Cerebellum: Brain for an Implicit Self (20 page)

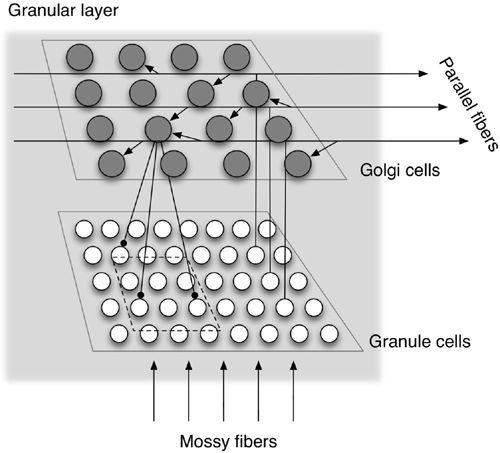
Figure 22. Ensemble patterns of granule cell discharge change continuously.

Shown are some results from a simulation study using the circuit shown in
Figure 21
. The temporal profile of activity is presented for 100 granule cells lined up along the ordinate. Each cell underwent random transitions between periods of active firing (solid lines) and rest (breaks in lines) during 1,000 time steps after mossy fiber stimulation. Because the various granule cells had different temporal active-inactive transition patterns, the ensemble pattern of active cells changed over time, and the same pattern did not appear more than once throughout the simulation period. Hence, there is a one-to-one correspondence between the ensemble pattern of active granule cells and a given time step within the simulated period. (From
Yamazaki and Tanaka, 2005
.)

In the resting state, climbing fibers discharge irregularly at a low rate (~1 Hz). When the inferior olive (IO) receives a stimulus, the rate of climbing fiber discharges increases or decreases transiently. This can be detected in peristimulus histograms after many repeated bouts of stimulation. IO neurons seem to recode the high-frequency information carried by their synaptic inputs in the resting state into stochastic, low-rate discharge (Schweighofer et al., 2004;
Kitazawa and Wolpert, 2005
). This keeps the probability low of conjunctive LTD occurring in Purkinje cells, that is, so that no learning occurs. When climbing fibers discharge at a higher rate locked to the stimulus pattern, conjunctive LTD is induced in those of the parallel fiber synapses that are undergoing correlated activation. The mechanism that switches between the resting and learning states appears to be based on gap-junction-mediated electrical synapses between IO neurons (
Chapter 6
, “
Pre- and Post-Cerebellar Cortex Neurons
”). Activity in these electrical synapses determines whether climbing fiber activity is rhythmic, random, or synchronous (
Kitazawa and Wolpert, 2005
).

An accessory circuit, composed of GABA-containing neurons located in the cerebellar nuclei, also regulates the activity of IO neurons. These GABA-containing neurons may modulate electrical synapses in
in vivo
neurons by the release of GABA, which has been shown to increase nonjunctional membrane conductance by shunting between the neurons. A computer simulation study showed that this inhibition of climbing fibers by cerebellar output combines with LTD/LTP to self-regulate spontaneous climbing fiber activity to an equilibrium level at which LTP and LTD are in balance and the expected net change in parallel fiber-Purkinje cell synaptic weights is at zero. This may be a unique network mechanism for regulating the modes of activation of
in vivo
neurons, and thereby regulate learning in cerebellar circuits (
Kenyon et al., 1998a
,
b
).

Another accessory circuit is the excitatory projection to the IO from certain midbrain neurons located from the rostral pole of the red nucleus to the caudomedial border of the thalamus. These neurons are located primarily in the parvocellular red nucleus, the nucleus of Cajal, the nucleus of Darkschewitsch, and the caudomedial extremity of the subparafascicular nucleus (
Saint-Cyr and Courville, 2004
). This accessory circuit may supply positive feedback to
in vivo
IO neurons, thereby antagonizing inhibition mediated by cerebellar nuclei.

These inhibitory and excitatory inputs to IO neurons (
Figure 23
) seem to modify the
in vivo
network that generates climbing fiber signals and hence regulates LTD-based learning. Heslow and Ivarsson (1996) demonstrated that cerebellar output during performance of a conditioned response inhibited the
in vivo
IO. Thus, studies of eye-blink conditioning have provided an opportunity to define the roles of the nucleo-olivary inhibitory projection, as explained in
Chapter 11
.

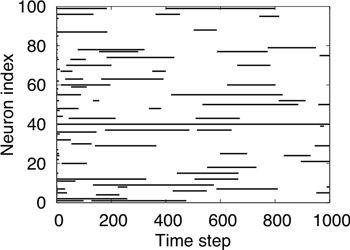
Figure 23. A microcircuit in the inferior olive.

Three IO neurons and their gap junction couplings are illustrated. “Half” junctions extending toward the outer edges indicate that the gap junction couplings include additional IO neurons that are not depicted in the drawing. Also illustrated are an excitatory and an inhibitory afferent. Some of the latter terminate precisely on the sites of gap junctions. Symbols: + in a circle, excitatory synapse; - in a circle, inhibitory synapse. (From
Bengtsson and Jörntell, 2009a
.)

Albus (
1971
) developed a simple perceptron model of the cerebellum based on the principle of a pattern-classification device (
Figure 6
). Later, he elaborated the model mathematically and proposed a cerebellar model articulation controller (CMAC) for application to engineering problems (
Albus, 1975
). He suggested that the mossy fiber to granule cell to Golgi cell input network performed an expansion recoding that enhanced the cerebellum’s pattern-discrimination capacity and the learning speed of Purkinje cells. Parallel fiber synapses of the dendritic spines of Purkinje cells, basket cells, and stellate cells were all postulated to have their own variable responses to climbing fiber activity. This variability was assumed to be the mechanism of pattern storage. Albus (
1971
) speculated further that in order for the learning process to be stable, pattern storage had to be accomplished principally by weakening synaptic weights rather than by strengthening them. This viewpoint was supported later by the finding of conjunctive LTD in the cerebellum.

In more general terms, a Purkinje cell in an adaptive filter model acquires a filtering function on the basis of multiple pairs of input signals (via parallel fibers) and corresponding desired output signals (via a climbing fiber). Adaptive filter models are advantageous in being able to accommodate temporally varying signals. This is not possible when using a simple perceptron model. Whereas a simple perceptron model is suitable for discrimination of spatial patterns of mossy fiber inputs, an adaptive filter model is better for recognition of the temporal patterns of these inputs. Indeed, an adaptive filter model has been shown to be effective for simulating adaptation in the VOR (
Fujita, 1982b
;
Dean et al., 2010
). As emphasized by Irry and Keele (
1989
), the cerebellum has a unique capability of timing to contribute to skills in general. This capability could arise from the adaptive filter network of the cerebellum.

A liquid state machine model has been proposed for describing computations in biological networks of neurons, particularly for adaptive computational systems (
Maass et al., 2002
). It provides a method for employing randomly connected circuits in meaningful computations. It also provides a theoretical context for heterogeneous, rather than stereotypical, local gates or processors to increase the computational power of a circuit. It is also a method for multiplexing different computations (on a common input) within the same circuit. Yamazaki and Tanaka (
2007
) applied such a model to the cerebellum. In
Figure 24
, external contextual information is fed to a network called a “reservoir,” in which a number of neuronal units are randomly connected to constitute a random recurrent network. The number of reservoir neurons is assumed to be much larger than that of afferent inputs so that the spatiotemporal activity pattern of reservoir neurons encodes afferent input signals in much higher dimensions. (“Dimension” refers to the number of parameters used to define the state of the network.) Then, the signals mapped in the reservoir and external error signals are fed to neuronal units called “readouts.” These readout neurons extract time-varying information using the error and produce the final output. It designates the functional role of the granular layer as a reservoir and the Purkinje cells as the generator’s readout neurons. It bears emphasis that a liquid state machine possesses a more powerful information processing capability than does a perceptron.

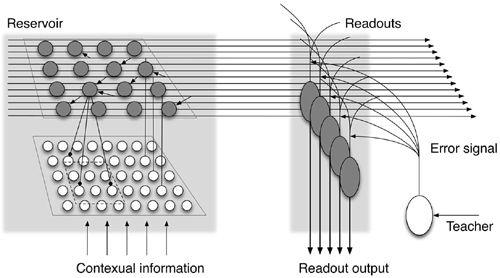
Figure 24. The structure of a liquid state machine model of the cerebellum.

This model shows external contextual information being fed to the recurrent network shown in
Figure 21
and called here a “reservoir.” It features a number of neurons that are connected randomly. In such a reservoir, the activity pattern of afferent input signals is represented by the population activity of reservoir neurons that evolves spatiotemporally. Because the number of reservoir neurons is assumed to be much greater than that of afferent inputs, the reservoir expands the dimension of input signals into a much higher one by means of the population activity of reservoir neurons. Another group of neurons called “readouts” receives the signals mapped in the reservoir (just as do Purkinje cells, and they also receive external error signals from teacher neurons in the IO. The readout circuit undergoes supervised learning by way of these external error signals and projects the desired signals (specified by the error signals) as the final output of the cerebellar cortex in response to the external contextual information. (Model of
Yamazaki and Tanaka, 2007
; courtesy of Tadashi Yamazaki.)

Evidence presented in
Chapters 8
,
10
, and
11
indicates that in addition to the cerebellar cortex, vestibular and cerebellar nuclei also provide memory sites. Why is such a dual memory system required? One prevailing view is that synaptic plasticity in the cerebellar cortex serves for quick and short-lasting adaptation that is needed from time to time, whereas synaptic plasticity in the nuclei sustains the memory required for slow and long-lasting adaptation. Another view is that relatively simple nuclear circuits are capable of retaining the memory of single parameters such as a gain increase or decrease but not the memory required for precise timing. The latter is presumably stored in more sophisticated cortical circuits. A role of nuclear memory in “savings” (the ability to relearn faster than the first time) has been demonstrated in modeling studies (Medina et al., 2001;
Masuda and Amari, 2005
).