The Clockwork Universe (24 page)

Chapter Forty
Talking Dogs and Unsuspected Powers

Leibniz gave the impression that he intended to pursue every
one of nature's secrets himself. “In the century of Kepler, Galileo, Descartes, Pascal, and Newton,” one historian wrote, “the
most versatile genius of all was Gottfried Wilhelm Leibniz.” The grandest topics intrigued him, and so did the humblest. Leibniz invented a new kind of nail, with ridged sides to keep it from working free. He traveled to see a talking dog and reported to the French Academy that it had “an aptitude that was hard to find in another dog.” (The wondrous beast could pronounce the French words for tea, coffee, and chocolate, and some two dozen more.)

He drew up detailed plans for “a museum of everything that could be imagined,” roughly a cross between a science exhibition and a Ripley's Believe It or Not museum. It would feature clowns and fireworks, races between mechanical horses, rope dancers, fire eaters, musical instruments that played by themselves, gambling halls (to bring in money), inventions, an anatomical theater, transfusions, telescopes, demonstrations of how the human voice could shatter a drinking glass or how light reflected from a mirror could ignite a fire.

Leibniz's energy and curiosity never flagged, but he could scarcely keep up with all the ideas careening around his head. “I have so much that is new in mathematics, so many thoughts in philosophy, so numerous literary observations of other kinds, which I do not wish to lose, that I am often at a loss what to do first,” he lamented.

Many of these ventures consumed years, partly because they were so ambitious, partly because Leibniz tackled everything at once. He continued to work on his calculating machine, for example, and on devising a symbolic language that would allow disputes in ethics and philosophy to be solved like problems in algebra. “If controversies were to arise, there would be no more need of disputing between two philosophers than between two accountants. For it would suffice to take their pencils in their hands, to sit down to their slates, and to say to each other (with a friend as witness, if they liked): ‘Let us calculate.' ”

Leibniz wrote endlessly, at high speed, often while bumping along the road in a coach. Today a diligent team of editors is laboring to turn well over one hundred thousand manuscript pages into a Collected Works, but they do not expect to complete the project in their lifetimes. Volume 4, to choose an example at random, comes under the heading of “Philosophical Writings,” and consists of three “books.” Each book contains over a thousand pages. The editors envision sixty such volumes.

Thinkers who take on the whole world, as Leibniz did, are out of fashion today. Even in his own era, he was a hard man to get the measure of. Astonishingly brilliant, jaw-droppingly vain, charming, overbearing, a visionary one minute and a self-deluded dreamer the next, he was plainly a lot of work. Not everyone was inclined to make the effort. Still, in Bertrand Russell's words, “Leibniz was one of the supreme intellects of all time.” If anything, his reputation among scientists and mathematicians has grown through the centuries, as ideas of his that once seemed simply baffling have come into focus.

More than three hundred years ago, for instance, Leibniz envisioned the digital computer. He had discovered the binary language of 0s and 1s now familiar to every computer programmer,
⁴⁶
and, more remarkably, he had imagined how this two-letter alphabet could be used to write instructions for an all-purpose reasoning machine.

The computer that Leibniz had in mind relied not on electrical signals—this was almost a century before Benjamin Franklin would stand outdoors with a kite in a lightning storm—but on marbles tumbling down chutes in a kind of pinball machine. “A container shall be provided with holes in such a way that they can be opened and closed,” Leibniz wrote. “They are to be open at those places that correspond to a 1 and remain closed at those that correspond to a 0. Through the opened gates small cubes or marbles are to fall into tracks, through the others nothing.”

Leibniz was born in Germany, but he spent his glory years in the glittering Paris of Louis XIV, when the Sun King had just begun building Versailles and emptying the royal treasury. Leibniz arrived in Paris in 1672, at age twenty-six, a dapper young diplomat sporting a long wig. The dark curls and silk stockings were standard fare, but the torrent of words that spilled forth from the new arrival dazed his listeners. Leibniz had come to Paris with characteristically bold plans. Germany dreaded an invasion by the French, who had grand territorial ambitions. Leibniz's mission was to convince Louis XIV that an incursion into Germany would do him little good. What he ought to do instead, what would prove a triumph worthy of so illustrious a monarch, was to conquer Egypt.

In four years Leibniz never managed to win an audience with the king. (France, as everyone had feared, spent the next several decades embroiling Europe in one war after another.) Leibniz spent his time productively nonetheless, somehow combining an endless series of visits with one count or duke or bishop after another with the deepest investigations into science and mathematics.

Leibniz's conquest of mathematics came as a surprise. Unlike nearly all the other great figures in the field, he came to it late. Leibniz's academic training had centered on law and diplomacy. In those fields, as well as philosophy and history and a dozen others, he knew everything. But at twenty-six, one historian writes, Leibniz's knowledge of mathematics was “deplorable.”

He would remedy that. In Paris he set to work under the guidance of some leading mathematicians, notably the brilliant Dutch scientist Christiaan Huygens. For the most part, though, he taught himself. He took up classic works, like Euclid, and recent ones, like Pascal and Descartes, and dipped in and out at random like a library patron flipping through the books on the “new arrivals” shelf. Even Newton had found that newfangled doctrines like Descartes' geometry slowed him to a crawl. Not Leibniz. “I read [mathematics] almost as one reads tales of romance,” he boasted.

He read voraciously and competitively. These were difficult, compact works by brilliant men writing for a tiny audience of peers, not textbooks meant for students, and Leibniz measured himself against the top figures in this new field. “It seemed to me,” he wrote shortly after beginning his crash course, “I do not know by what rash confidence in my own ability, that I might become the equal of these if I so desired.” The time had come to stop reading about what other people had done and to make discoveries of his own.

By now it was 1675. Leibniz was thirty but still, at that advanced mathematical age, at the peak of his powers. The riddle that taunted every mathematician was the infinitesimal, the key to understanding motion at a given instant. Nearly a decade before, Newton had solved the mystery and invented what is now called calculus. He had told almost no one, preferring to wrap that secret knowledge around himself like a warm cloak. Now, unaware of what Newton had already done, Leibniz set out after the same prize.

In the course of one astonishing year—a miracle year of his own—he found it. Newton had kept his discovery to himself, because of his hatred of controversy and because the security of his professorship at Cambridge meant he did not have to scramble for recognition. Leibniz did not publish an account of his discovery of calculus for nine years, but his silence is harder to explain. Leibniz never had a safe position like Newton's. Throughout his long career, he was dependent on the whims of his royal patrons, forever trapped in the role of an intellectual court jester. That might have made him
more
eager to publish, anything to make his status less precarious, but it did not.

The reasons for his delay have disappeared into a biographical black hole. Leibniz wrote endlessly on every conceivable topic—his correspondence alone consisted of fifteen thousand letters, many of them more essays than notes—but he remained silent on the question of his long hesitation. Scholars can only fill the void with guesses.

Perhaps he was gun-shy as a result of a fiasco at the very beginning of his mathematical career. On his first trip to England, in 1672, Leibniz had met several prominent mathematicians (but not Newton) and happily rattled on about his discoveries. The bragging was innocent, but Leibniz was such a mathematical novice that he talked himself into trouble. At an elegant dinner party in London, presided over by Robert Boyle, Leibniz claimed as his own a result (involving the sum of a certain infinitely long sequence of fractions) that was in fact well-known. Another guest set him straight. In time the episode blew over. Still, Leibniz may have decided to make sure that he stood on firm ground before he announced far bolder mathematical claims.

Or perhaps he decided that formal publication was beside the point because the audience he needed to reach had already learned of his achievement through informal channels—rumors and letters. Or the task of developing a full-fledged theory, as opposed to a collection of techniques for special cases, may have proved unexpectedly difficult. Or Leibniz may have judged that he needed to make a bigger splash—from an impossible-to-miss invention like the telescope or from some diplomatic coup—than any mathematical discovery could provide.

Eventually, in 1684, Leibniz told the world what he had discovered. By then he and Newton had exchanged friendly but guarded letters discussing mathematics in detail but tiptoeing around the whole subject of calculus. (Rather than tell Leibniz directly what he had found, Newton concealed his most important discoveries in two encrypted messages. One read, “6accdae13eff7i319n4o4qrr4s8t12ux.”) In the published article announcing his discovery of calculus, Leibniz made no mention of Newton or any of his other predecessors.

In the case of Newton, at least, that oversight was all but inevitable, since Leibniz had no way of knowing what Newton had found. A perfect alibi, one might think, but it proved anything but. Leibniz's “oversight” was destined to poison the last decades of his life.

Chapter Forty-One
The World in Close-Up

Newton and Leibniz framed their discoveries in different vocabulary, but both had found the same thing. The challenge confronting both men was finding a way to stop time in its tracks. Their solution, hundreds of years before the birth of photography, was essentially to imagine the movie camera. They pictured the world not as the continuous, flowing panorama we see but as a series of still photos, each one barely different from those before and after it, and all the frames flashing before the eye too quickly to register as static images.

But how could you be sure that, no matter what moment you wanted to scrutinize, there happened to be a sharply focused image on hand? It seemed clear that the briefer the interval between successive still photos, the better. The problem was finding a stopping place—if sixty-four frames a second was good, wouldn't 128 be better? Or 1,000, or 100,000?

Think of Galileo near the top of the Leaning Tower, a bit winded from the long climb. He extends an arm out into space, opens his fingers, and releases the rock he has lugged up all this way. It falls faster and faster—in each successive second, that is, it covers more distance than it did the second before—as the figures in this table show. (As we have seen, it was no easy matter to make such measurements without clocks or cameras, which was why Galileo ended up working with ramps rather than towers.)

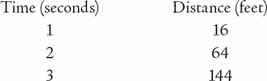
Galileo found that rocks fall according to a precise rule that can be expressed in symbols. Scientists write the rule as
d
= 16
t
²
, where
d
stands for distance and
t
stands for time. In one second, a rock falls a distance of 16 × 1 feet, or 16 feet. In two seconds, it falls a distance of 16 × 4 feet, or 64 feet; in three seconds, 16 × 9 feet, or 144 feet.

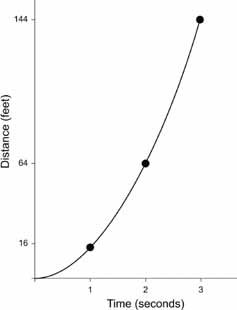
The graph shows how far a rock dropped from a height falls in t seconds. The rock obeys the rule d = 16 t
²
.

The table can be converted to a graph, and, as usual, a picture helps reveal what the numbers only imply. (And a picture, unlike a table, shows the rock's position at
every
moment rather than at a select few.) The horizontal axis depicts time, the vertical axis distance. The drawing shows the distance the rock has fallen at a given time. At the moment that Galileo uncurled his fingers and released the rock (in other words, at
t
= 0), the rock has fallen 0 feet. At 1 second it has fallen 16 feet; in 2 seconds, 64 feet; and so on.

The transition from rock to table to graph is one of increasing abstraction, and early mathematicians had a hard time keeping their bearings. Few things could be more tangible than a rock. When Galileo let it go, anyone who happened to be passing by could see it. The table took that ordinary event—a stone whooshing toward the ground—and transformed it into a list of numbers. The graph represented still another move away from everyday reality. It shows a curve that represents the rock's distance from Galileo's hand, but the curve in the graph only matches the real-life descent of the falling rock in a subtle way. The actual rock dropped in a straight line. The graph shows a curve, a parabola. Worse yet, the rock fell
down
, while the parabola headed
up
. To “see” the rock falling in the way that the graph depicts required a far more laborious and roundabout process than merely looking at a rock.

And yet it was this second way of looking at a rock's fall, this unnatural way, that held the key to nature's secrets. For it was this curve that showed Newton and Leibniz how to seize time in their fists and hold it still. We saw in chapter 36 that in a graph that shows distance measured against time, a straight line corresponds to a steady speed. (The greater the speed, the steeper the slope of that line, because a steeper slope indicates more distance covered in a given amount of time.) But in the graph of a falling rock, we have a curve, not a straight line. How can we talk about the rock's speed? In particular, how can we find its speed at a specific instant, at, for instance, precisely one second into its fall?

We could do it, Newton and Leibniz explained, if we could find the slope of the curve at precisely the one-second point. Which they proceeded to do. The idea was to look at the curve in extraordinary close-up. If you look closely enough, a curve looks like a straight line. (A jogger on a huge circular track would feel as if she were running in a straight line. Only a bird's-eye view would reveal the track's true shape.) And although curves are hard to work with, straight lines are easy.

First they froze time by selecting a single frame from nature's ongoing movie. (Newton and Leibniz worked in parallel, unaware of one another, as we have seen, but they independently hit on the same strategy.) Second, they tunneled into that frame, as if it were a slide under a microscope.

In the case of a falling rock, they began by freezing the picture at the instant
t
= 1 second. They wanted to know the rock's speed at that moment, but the only information they had to work with was a graph depicting time and distance. Even so, they were nearly done.

All they had to do was focus their conceptual microscope. Speed is a measure of distance traveled in a given time.
Sixty miles per hour
.
Three inches per second
. To solve the problem they cared about, they began by solving an easier problem, in the hope that the solution to the easy problem would point to the solution they truly wanted.

The rock's speed at a given instant was hard to find because that speed was constantly changing. But the rock's
average
speed over any particular span of time was easy to find. ( Just divide the distance the rock fell by the length of the time span.) With that in mind, Newton and Leibniz did something clever. They put the actual rock to one side for a moment and concentrated instead on an easier-to-deal-with imaginary rock. The great virtue of this imaginary rock was that, in contrast with a real rock, it fell at a constant speed. What speed to pick?

The answer, Newton and Leibniz decided, was that the imaginary rock should fall at a steady speed that exactly matched the average speed of the actual rock in the interval between
t
= 1 and
t
= 2. This roundabout procedure seems like a detour, but in fact it brought them closer to their goal.

Look at the graph below. The dotted line depicts the imaginary rock, the curve the real rock. At the one-second mark (in other words, at
t
= 1) the imaginary rock and the real one have both fallen 16 feet. At
t
= 2, both the imaginary rock and the real one have fallen 64 feet.

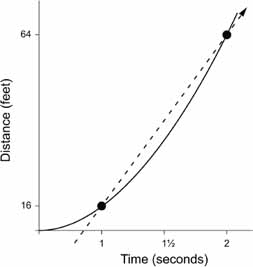
The dotted line represents the fall of an imaginary rock traveling at constant speed. The slope of the dotted line gives the imaginary rock's speed in the one-second interval between t = 1 and t = 2.

The dotted line is straight. That's crucial. Why? Because it means we can talk about its slope, which is a number—a regular, run-of-the-mill number, not an infinitesimal or any other colorful beast. That number is the speed of the imaginary rock. (It is easy to compute. Slope is a measure of steepness, which means that it is a ratio of vertical change to horizontal change. In this case, the vertical change was from 16 feet to 64 feet, and the horizontal change was from 1 second to 2 seconds, so the slope was [64–16] feet
÷
[2–1] seconds, or 48 feet per second.)

Now Newton and Leibniz made their big move. Forty-eight feet per second was the imaginary rock's speed over a one-second span. That gave a fair approximation to what they really wanted to know about, an actual rock's speed at the precise instant
t
= 1.

How could you get a better approximation? By zooming in for a closer look at the graph. And the way to do that was once again to focus your attention at
t
= 1 but this time to look at a shorter time interval than one second. As usual, pictures came to the rescue.

Look at the diagram below. The new, dashed line represents the path of a new imaginary rock.
This
imaginary rock, too, is falling at a constant speed. What speed? Not the same speed as the first imaginary rock. This new imaginary rock is falling at a speed exactly equal to the actual rock's average speed in a newer, shorter time interval, the interval between
t
= 1 and
t
= 1
½
. The point is that the speed of this new imaginary rock gives us a better estimate of the actual rock's speed at the instant
t
= 1.

* * *

The dashed line represents the fall of a new imaginary rock. The slope of the line gives the imaginary rock's speed, which is constant, in the one-half second interval between t = 1 and t = 1 ½.

If we zoomed in on an even shorter interval starting at
t
= 1, we could draw still another straight line. We might, for instance, focus on the interval between
t
= 1 second and
t
= 1
¼
seconds. The new line, too, would have a slope that we could compute. We could repeat the procedure still another time, this time focusing on a yet-shorter interval, say between
t
= 1 second and
t
= 1
⅛
seconds. And so on.

Newton and Leibniz saw that you could continue drawing new
straight lines
forever.
Pictorially, you would be drawing straight lines that passed through two dots on the curve. One dot was
fixed in place at
t
= 1, and the other moved down the curve, like a
bead on a wire, approaching ever nearer to the fixed dot.

Those lines would approach ever nearer to one particular straight line. That “target” line was unique, in a natural way—it was the line that just grazed the curve at a single place, the point corresponding to
t
= 1. The target line—in mathematical jargon the tangent line—was the prize that all the fuss was about. (In the diagram below, the tangent line is the straight line made up of short dashes.) Until this moment, mathematicians had never managed to close their fingers around the notion of instantaneous speed. Now they had it.