The Source Field Investigations (49 page)

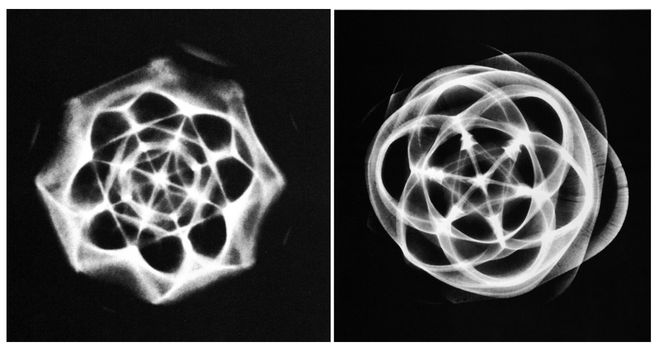
Dr. Hans Jenny found that particles floating in a liquid naturally arranged into different geometric patterns depending on the frequency of vibration he introduced.

By 1996, I had already realized that geometry must be the big secret to understanding energy, matter, the mechanisms responsible for biological life, and even consciousness—although I didn’t find the proof in Jenny’s work until later on. If we want to find out exactly what coherence looks like in a fluid, we look no further than these five basic Platonic solids—the tetrahedron, cube, octahedron, icosahedron and dodecahedron. Mathematicians already know these shapes have more symmetry, as in more coherence, than any others. Simply put, each of them will fit perfectly in a sphere, and each point is equidistant from its neighbors. Each side of the geometry has the same shape, and every internal angle will also be the same.

Physicists were always looking for the missing link that could unify the very large with the very small. Now that there were clear and obvious geometric patterns in the earth, it seemed very likely that if we are truly dealing with a unified field model, the patterns we see on a larger scale would also appear in quantum mechanics. Atoms, rather than being a bunch of seemingly solid particles whirling around a nucleus, could now be reimagined as geometric patterns of flow—within the fluidlike energy of the Source Field. When you increase the frequency of vibration, the geometry becomes more complex. Once we understand how this principle really works, it might also lead to the transmutation of elements—such as the classic alchemist’s dream of turning lead into gold.

Where do we start, then? In Larson’s model, if we’re looking for geometry within the atom, all we have to do is study the nucleus—as he feels the nucleus is the atom: “In
The Case against the Nuclear Atom,
Larson . . . points out that, in fact, the ‘size’ of the nucleus . . . is rather the size of the atom itself.”
³⁵
Larson’s model did not have geometry in it—but Nehru also admits they haven’t worked all the kinks out yet.

The first scientist I found who had a working quantum physics model, based entirely on geometry, was Rod Johnson—who posted intriguing concepts on Richard C. Hoagland’s discussion forum back in 1996. In the ensuing years, I have interviewed him extensively and published the results on my Web site, Divine Cosmos—and unfortunately he passed away in 2010
.
I was stunned at how many mysteries of quantum mechanics he could explain with geometry—including Planck’s Constant, the Fine Structure Constant, the ratio between the weak force and the strong force, the structure of the photon, and others.
³⁷
Without ever knowing about Larson’s model, Johnson independently developed a similar concept. In Johnson’s model, there was indeed a parallel reality that is constantly intersecting with our own in every atom, at the tiniest level. Every atom had one geometry in our reality, and an opposite, inverse geometry in the parallel reality. The two geometries then counter-rotated inside of each other. Each stage of this process carried you through the different elements. Clearly, Johnson had a great model, although he didn’t have enough specifics to resolve the entire Periodic Table yet—but he felt all the answers could be found in James Carter’s theory of circlons.
³⁸

Later on I found Dr. Robert Moon, who could explain everything in the Periodic Table with geometry. He was one of the key scientists involved in the Manhattan Project, which developed the world’s first controlled thermonuclear fission reaction. He was the second scientist ever to build a cyclotron in the 1930s, and significantly improved the first—which had been built by E. O. Lawrence. In the Manhattan Project, Dr. Moon solved critical problems to make the first atomic pile possible, and built the first scanning X-ray microscope after World War II. From 1974 until his death in 1989, he was a key collaborator with Lyndon H. LaRouche, Jr.
³⁹
A variety of articles on his new quantum physics model can be found at LaRouche’s 21st Century Science and Technology Web site.
⁴⁰

In 1986, Dr. Moon finally realized that geometry was the key to understanding quantum physics—and it was a geometry in time as well as in space. That means that when you move through space, or time, you must move through geometry. You can’t just move in a nice, smooth, even curve—you have to pop through one quantity of space, or one quantity of time, before you can go to the next one. The scientific word for this kind of movement is that it would be
quantized
. Dr. Moon outlined his concept that space and time are quantized in a lecture from 1987.

The Platonic solids, of course, are all the same geometries we’ve been discussing here—the tetrahedron, cube, octahedron, icosahedron and dodecahedron. The details are quite technical, but here’s the gist of what Dr. Moon found: The same geometric shapes we see in the expansion of the earth also appear within the nucleus of the atom. Furthermore, in Moon’s model, more than one geometric form can nest within the nucleus at the same time—each one inside the next. This geometry actually determines how many protons our scientists will find in any one atom. The trick is to count the number of points on each of the so-called Platonic solids. There are eight points on a cube, six on an octahedron, twelve on an icosahedron and twenty on a dodecahedron, for a total of forty-six. In Moon’s model, that’s the first half of the naturally occurring elements in the Periodic Table. Moon knew there are a total of ninety-two elements that appear in nature, or two times forty-six—so he believed that every atom with an atomic weight of forty-seven or higher was a combination of two nests of geometry connected side by side, growing increasingly unstable along the way.
⁴²

You may have noticed Dr. Moon did not include the tetrahedron in this grouping. He feels that since the geometric opposite of the tetrahedron is still a tetrahedron, it plays a different role. Indeed, in Rod Johnson’s model as well as Buckminster Fuller’s earlier model, a photon appears as two tetrahedrons back-to-back—and we have the solid data to prove it in Planck’s Constant.
⁴³

Anyway, some very cool things happen when you use Moon’s model. The first completed shell in the nucleus is the cube, with eight protons. This corresponds to oxygen, which is highly stable—and makes up 62.55 percent of all the atoms in the earth’s crust. It is also interesting that oxygen is one of the single most important elements to sustain life. The second completed shell is the octahedron, with fourteen protons—and now you have silicon, which comes in at 21.22 percent. Although we are considered carbon-based life-forms, silicon is also very important for biological life—and seems to be the key ingredient in the spontaneous generation experiments, such as Dr. Ignacio Pacheco’s work with the silicon in beach sand.

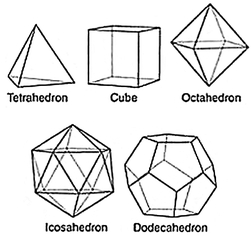
Dr. Robert Moon discovered that the protons of atoms naturally assemble into the Platonic solids, as seen here. Each proton corresponds to a vertex of the geometry.

So, between these first two shells alone—oxygen with a cubical nucleus and silicon with an octahedron-shaped nucleus—you have 84 percent of all the atoms in the earth’s crust. Then, when you move up to complete the next shape, the icosahedron, you now have twenty-six protons. This is the iron atom, which is the best metal we have for creating naturally occurring magnetic fields. This hidden geometric symmetry may very well be responsible for iron’s magnetic properties—by acting as a conduit for the Source Field, as we will discuss. Of all the atoms in the earth’s crust, 1.20 percent are iron, but they add up to 5 percent of the total weight. Then, the dodecahedron fills up at forty-six protons, and you now have palladium—which is an unusually symmetrical atom that was used in all the cold fusion experiments. And in case you think cold fusion was all just a waste of time, don’t forget that Dr. Eugene Mallove resigned from his position as the chief editor of MIT’s technical newsletter when he allegedly discovered they were falsifying their own data on cold fusion—as if to say there was no effect.
⁴⁴

According to a paper by Laurence Hecht, Moon’s model satisfies all sorts of quantum puzzles—including the processes of fission and fusion, the mystery period of fourteen for the rare earth elements, the exact number of elements in each row of the Periodic Table, and Maria Goeppert-Mayer’s Magic Numbers, in which the properties of the nucleus tend to suddenly change at certain numbers that curiously reappear—whether you’re looking at protons, neutrons or the mass number.
⁴⁵
Hecht has continued developing and refining Moon’s model ever since Moon’s death in 1989.
⁴⁶

I was even more impressed when I found out that atoms naturally gather together into these exact same geometric patterns when they are set loose, one at a time, in a given area. These are called microclusters, and they are completely baffling to mainstream scientists. The microcrystals floating in the pineal gland may be similar—albeit larger. A 1989 issue of
Scientific American
revealed that microclusters do not have characteristics like liquids or gases.

I then found the college textbook
Microcluster Physics
by Satoru Sugano and Hiroyasu Koizumi, which revealed even more—including compelling images of the geometry.
⁴⁸

Microclusters can be anywhere between ten to a thousand atoms. The strangest thing about them is that the electrons appear to orbit the center of the cluster, rather than the center of each individual atom. Of course, this weird behavior suggests there are no electrons. Instead, what scientists actually see is geometrically arranged electron clouds, which appear to be where the fluidlike flow of the Source Field enters into the atom. Once some of this stored energy is released from the atom, it turns into a photon—which then looks like a particle. Microclusters are also called “monatomic elements” or “ORMUS elements” in various sources—elegantly summarized in Lawrence Gardner’s
Lost Secrets of the Sacred Ark.
⁴⁹
Microclusters appear to display gravitational anomalies, including levitation, under certain circumstances—as well as superconductivity. Ancient peoples believed that ingesting microcluster gold would awaken their pineal glands—and the Egyptians even stored it in cone-shaped cakes.
⁵⁰

Yet another tantalizing clue that atoms are geometric patterns within a fluidlike energy flow is the phenomenon of quasi-crystals. In this case, you have crystals that look just like the Platonic solids we’ve been discussing, including the dodecahedron—along with other forms. They are created by supercooling certain combinations of molten metals at a very fast speed—apparently capturing the molecules while they are flip-flopping between space-time and time-space, and freezing them into a half-in, half-out crystal pattern. The problem is that these crystals destroy all the known rules of crystal formation—they should not be able to exist, because you cannot build perfect five-sided crystals out of atoms that are made of particles.
⁵¹