X and the City: Modeling Aspects of Urban Life (3 page)

In Greek mythology, Dido was a Phoenician princess, sister of Pygmalion, King of Tyre, and founder of the city of Carthage in northern Africa in 814 B.C. According to tradition, she did this in a rather unusual way. Pygmalion had her husband, Sychaeus, killed, and Dido fled to the northern coast of Africa. According to some, her brother agreed to let her have as much land as she could enclose within the hide of a bull; according to others, she bartered with the locals to accomplish this. She then cut the hide into a series of thin strips, joined them together, and formed a semicircular arc, with the Mediterranean Sea effectively as a diameter, thus enclosing a semicircular area [
4
]. Bravo! As we shall note in
Appendix 1
, given a straight boundary (as assumed in this story), a semicircle will contain the maximum area for a given perimeter, so Dido achieved the best possible result!

I grew up the son of a farm-laborer and had the occasional less-than-pleasant encounter with a certain bull; although he was British he was certainly not a gentleman. Here’s how the mathematics might have gone. Imagine the typical bull torso to be a rectangular box 5 ft long by 4 ft high by 2 ft wide. (Yes, that’s correct, we’ve cut off his legs, head, and tail, but only in our imagination.) The surface area of our bull-box is readily shown to be about 80 sq ft. We’ll round this up to 100 sq ft since we’re only interested in a rough estimate. And anyway, given how shrewd Dido appeared to be, no doubt she would have picked the biggest bull she could find! I don’t know what kind of precision Dido or her servants might have had with the cutting tools available but I’m going to assume that strips could be cut as narrow as one hundredth of a foot (0.12 in, or about 3 mm). This may be an underestimate, but it makes the arithmetic easier without changing the “guesstimate” by much. If the total length of the strips is
L
ft, then we have a simple equation for the area: 0.01
L
≈ 100, or
L
≈ 10
⁴
ft. This length would comprise the semicircular part of the city boundary. For a radius
r
ft,

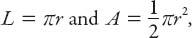
where
A
is the area of the “city.” Hence

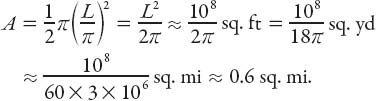
This is about 1.6 km
²
. That’s pretty impressive for a load of bull! If the boundary were circular instead of semicircular, the corresponding area would be half this amount, or about one third of a square mile. In
Appendix 2
we shall generalize this idea to the case in which the boundary is of variable length
l
<
L
.

Let’s return to part of the quotation from John of Patmos (stated at the beginning of this book). He was in exile on the island of Patmos, off the west coast of Turkey, probably around 90–95 A.D. Recall that, according to one translation, “He found out that the city was as wide as it was long and it was as high as it was wide. It was as long as a man could walk in fifty days.” Another translation says that “it was twelve thousand furlongs in each direction, for its length, breadth and height are all equal.” A furlong is 220 yards, there being eight in a mile, so the city was a cube 1,500 miles on a side. Perhaps with windows and doors and open spaces it was like a Menger sponge! (See
Appendix 9
.)

Question:
How far might an adult walk in those days without the benefit of modern transportation?

I want to estimate this one! At 3 mph for 10 hours, 30 miles a day for 50 days is, guess what, 1,500 miles!

Question:
What was the volume of the heavenly city in John’s vision? In cubic miles? In cubic kilometers? In cubic furlongs? Estimate how many people it could accommodate.

An estimation question that can be generalized from the rest of the quotation—the number of leaves on a tree—can be found in
Chapter 5
.

Before we can explore mathematics in the city, we need to get there. The fastest way is to fly, so let’s hop on a plane. If we assume that the descent flight path occurs in the same vertical plane throughout (i.e., no circling before touchdown—which is very rare these days), then the path is quite well represented by a suitably chosen cubic function [
5
], as we will see below. Here are some further conditions we impose prior to setting up a mathematical model for the path:

(i) The horizontal airspeed
dx/dt
=
U
is constant throughout the descent. This is somewhat unrealistic, but we’ll work with it anyway.

 (ii) The descent begins when the plane is at the point (−
L
,
h
), the origin being the beginning of the runway.

(iii) The magnitude of the vertical component of acceleration must not exceed the value
k
, where 0 ≤
k
g
,
g
= 32.2 ft/sec
²
being the acceleration due to gravity.

(iv) The plane is considered for simplicity to be a point mass. The ultimate in cramped seating!

The landing path is modeled by

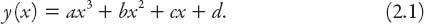
What kind of boundary conditions should be imposed? Well, we would like to have a smooth touchdown, which means that not only do the wheels of the plane touch the runway at landing, they should have no downward component of velocity as they do so.
That’s
the kind of landing that generates applause from the passengers! And at the beginning of the descent we would like to move smoothly down toward the airport, so a similar set of conditions applies, namely, that

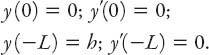
Exercise:
Show that these conditions imply that the equation of the flight path is

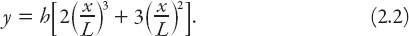
A graph of
Y
=
y/h
vs.
d
=
x/L
is sketched in
Figure 2.1
.

The vertical component of the airplane’s velocity is