X and the City: Modeling Aspects of Urban Life (8 page)

where the distance
d
(
x
,
y
) from a particular mall is calculated using the standard Pythagorean distance formula. The two malls
A
and
B
will be located at the coordinate origin and at (
b
, 0), respectively. We wish to determine the locus of points in the (
x
,
y
)-plane such that
N
₁
=
N
₂
. This will be the (closed) boundary curve inside and outside of which one mall is preferred over the other. Therefore we can write

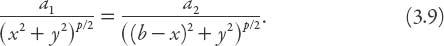
Rearranging this equation by raising both sides to the power 2/
p
we obtain

where the positive parameter
k
= (
a
₁
/
a
₂
)
^2/
p
. In so doing we have effectively transferred the dependence on the distance (via the parameter
p
) to a measure of the “relative attractiveness” of the malls. For given values of
a
_i
, note that
k
increases as
p
decreases toward zero if
a
₁
/
a
₂
> 1, and
k
decreases as
p
decreases toward zero if
a
₁
/
a
₂
> 1, and
k
decreases as
p
decreases toward zero if
a
₁
/
a
₂
< 1. Upon completing the square it follows that for
k
≠ 1

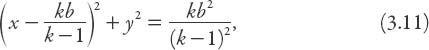
that is, the “boundary of attraction” is a circle of radius
centered at the point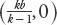
. If 0 <
k
< 1, that is, mall
A
is considered less attractive than mall
B
, the center of the boundary is on the negative
x
-axis. Furthermore, in this case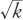
>
k
so that the circle extends into the half-plane and the point closest to mall
B
is
at a distance
from it. If
k
> 1, mall
A
is the more attractive of the two, and the closest point on the boundary to the point
A
is also a distance
from it.
Figure 3.7
illustrates this case for arbitrary
k
> 1; the dotted contours represent circular arcs on which (i)
N
₁
is constant (outside the solid circular boundary) and (ii)
N
₂
is constant (inside the boundary), respectively.

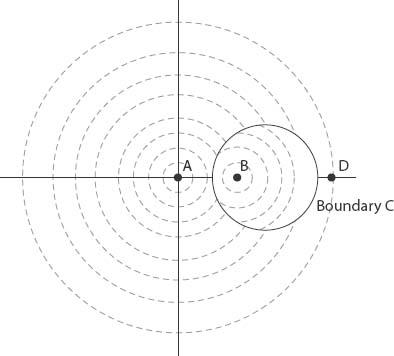
Figure 3.7. Equidistance contours and “attraction” boundary for a circular city.

One obvious and simple change to the model would be to consider elliptical contours of constant
N
_i
; thus for the equation of the boundary curve we might use

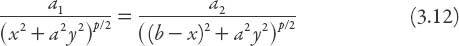
instead of equation (3.9). In this case, if
a
> 1 the loci of constant
N
_i
will be ellipses with semi-major axes along the
x
-axis, and the resulting boundary curve is also an ellipse, not surprisingly, with the equation