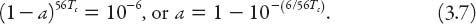X and the City: Modeling Aspects of Urban Life (6 page)

Figure 3.1. Display geometry for the maximum viewing angle. The object (e.g., a painting) lies along the vertical segment
AB
.

This is posed as a standard optimization problem in many calculus books. Consider the object of interest to be of vertical extent
h
(from
A
to
B
) with its base a distance
Y
above the observer’s eye line (the
x
-axis, with the observer at the origin
O
). From
Figure 3.1
it is clear that the angle
AÔB
=
θ
=
α
−
β
is to be maximized. If
A
has coordinates (
x
,
Y
) in general, it follows that

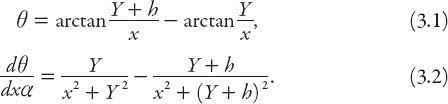
Therefore an extremum occurs when

Y
[
x
²
+ (
Y
+
h
)
²
] = (
Y
+
h
)(
x
²
+
Y
²
), i.e., when
x
= (
Y
²
+
Yh
)
^1/2
≡
X
.

We know this corresponds to a maximum angle, so we leave it to the reader to verify that
θ
″(
X
) < 0. For the Statue of Liberty, the plinth height
Y
is 47 meters, and the Lady herself is almost as tall:
h
= 46 meters. Therefore if the ground is flat we need to stand at a distance of
X
= (46 × 47 + 47
²
)
^1/2
= 66 meters.

It is interesting to verify that the points
O, A
, and
B
lie on a circle: if this is the case, the center of the circle has coordinates (0,
Y
+
h
/2) by symmetry. Then if the radius of the circle is
r
it follows that

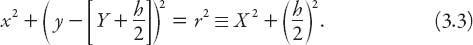
It is readily verified that the points
A
(
X
,
Y
),
B
(
X
,
Y
+
h
), and
O
(0, 0) all satisfy this equation, so the eye level of the observer is tangent to the circle. And another interesting fact is that this maximum angle is attained from any other point on the circle (by a theorem in geometry). Of course, this is only useful to the observer if she can levitate!

This result for the “vertical” circle (
Figure 3.1
) has implications for a “horizontal” circle in connection with the game of rugby—the best position to place the ball for conversion after a try is on the tangent point of the circle (see the book by Eastaway and Wyndham [
8
] for more details; they also mention the optimal viewing of two other statues—Christ the Redeemer in Rio de Janeiro and Nelson’s Column in London).

We have tickets to the symphony. It is well known that the “acoustics” in some concert halls are better than in others—a matter of design. A fundamental question in this regard is—how long does it take for a musical (or other) sound to die out? But this is a rather imprecise question. As a rough rule of thumb, for the “average” (and hence nonexistent) person, weak sound just audible in a quiet room is about a millionth as intense as normal speech or music, so we’ll define the reverberation time
T
in seconds as the time required for a sound to reach 10
⁻⁶
of its original intensity (Vergara 1959). Clearly, the value of
T
depends on many things, particularly the dimensions of the room and how well sound is absorbed by the wall, floor, ceiling, and the number of people present. Suppose that as the sound is scattered (here meaning reflected and absorbed) and the average distance between reflecting surfaces is
L
feet. On encountering such a surface suppose that (on average) a proportion
a
of the intensity is lost. We will call
a
the
absorptivity
coefficient. If the original sound intensity is
I
₀
, then the intensity after
n
reflections is

We’ll assume this to be an exact expression from now on. Then we naturally ask: when does
I
_n
= 10
⁻⁶
I
₀
? In other words, if (1 −
a
)
ⁿ
= 10
⁻⁶
, what is
n
(to the nearest integer)? It is convenient to work with common logarithms here, so

(to the nearest integer). If
c
(ft/s) is the speed of sound in air at room temperature and pressure, then on average over a distance
L
, sound will be reflected approximately
c/L
times per second. This enables us to write the reverberation time
T
as

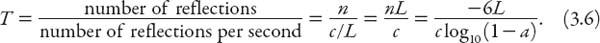
T
is a linear function of
L
as we would expect, but before putting in some “typical” numbers, let’s see how the quantity
N
=
n
/6 =
Tc/6L
= −[log
₁₀
(1 −
a
)]
⁻¹
behaves as a function of the absorptivity
a
.

It can be seen from
Figure 3.2
and equation (3.6) that both
n
and
T
fall off rapidly for absorptivities up to about 20%. In fact, if we use
c
≈ 1120 fps and
L
≈ 20 ft, then
n
≈ 270 and therefore the number of reflections per second is
c/L
≈ 56 s
⁻¹
. This means that
T
≈ 5 s, which is an awfully long time—almost long enough for the audience to leave the symphony hall in disgust! We need to do better than this. This is why soundproof rooms have walls that look like they are made of egg cartons: the value of
a
needs to be much higher than 0.05.

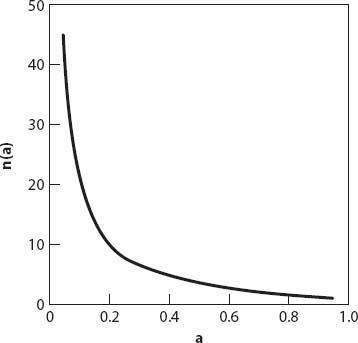
Figure 3.2. The reflection function
n
(
a
).

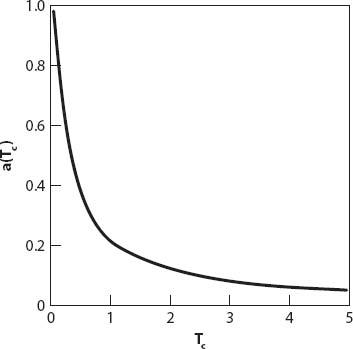
Figure 3.3. Absorptivity as a function of threshold reverberation time
T
_c
.

However, we can invert the problem: suppose that the musicologists and sound engineers have determined that
T
should be no larger than
T
_c
seconds. With the same values of
c
, and
L
, we now require that
n
= 56
T
_c
, so that