X and the City: Modeling Aspects of Urban Life (61 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

The angular dependence of the polarization for unpolarized incident light is conveniently expressed in terms of the quotient
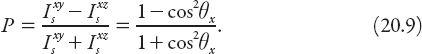
The graph of
P
is shown in
Figure 20.6
(in Cartesian form with
θ
x
in radians), illustrating afresh that (for
ideal
molecular scatterers) the light is 100% polarized at 90° to the incoming radiation and completely unpolarized in the
forward (0°) and backward (180°) directions. (In practice this will not be the case because molecules are not perfect scatterers [
36
].)
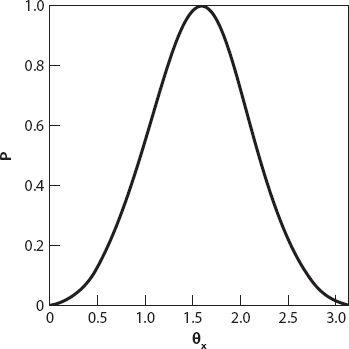
Figure 20.6. Degree of polarization for unpolarized incident light as given by equation (20.9).
We have stated that the results above for Rayleigh scattering apply when the particle size is much less than the wavelength of incident light, that is,
R/λ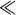 1. But what does the phrase “much less” really mean? There is no universal definition, and as usual, it depends on the context. Several books and articles on the topic of scattering use the inequality
1. But what does the phrase “much less” really mean? There is no universal definition, and as usual, it depends on the context. Several books and articles on the topic of scattering use the inequality
R
<
λ
/20, or even
R
<
λ
/10, and we shall be content with this. Since the wavelength of visible light lies in the range 400–800 nm (0.4
μ
–0.8
μ
), this means that
R
< 0.04
μ
should suffice.
For particles larger than this the processes of reflection, refraction, and diffraction cannot be neglected. It turns out that most of the light is scattered near the forward direction, but for particles whose size is comparable with the wavelengths of light, the situation is quite complex (but very interesting!) both mathematically and physically. The exact solution to this problem for spherical particles is often referred to as the Mie solution, from a 1908 paper by Gustav Mie; Debye also solved the problem independently in 1909, but the solution had already been published in 1863 by Clebsch, and again independently by Lorenz in 1890 and 1898. The rediscovery of existing results is a rather common theme in the history of science and mathematics.
The total amount of light scattered by a spherical particle is quite sensitively dependent on
R
/
λ
as already noted. This dependence can be characterized by a quantity
C
s
, the
scattering area coefficient
. It is defined to be the amount of light that would be intercepted by a particle (not necessarily a sphere) of cross-sectional area
C
s
πR
2
. If, for example, the particles are very small, that is,
R
/
λ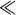 1, the dominating mechanism is Rayleigh scattering, with its dependence on
1, the dominating mechanism is Rayleigh scattering, with its dependence on
R
6
(or
V
2
, see equation (20.8)), then
C
s
will increase as (
R
/
λ
)
4
initially. For scattering by sufficiently large particles,
C
s
approaches two. This is the source of a fascinating paradox,
the extinction paradox
: why is
C
s
not equal to one? The debate involves some very sophisticated mathematical physics that will not be discussed here except to say that it involves interactions between the external and internal radiation fields of the particle. However, it should be pointed out that the paradox has not been entirely resolved if recent literature on the topic is anything to go by!
Figure 20.7
shows a graph of
C
s
vs. 2
πR
/
λ
(the ratio of circumference to wavelength) for a spherical particle with the same density as water. As noted above,
C
s
rises toward its first (and largest) maximum, it does so initially as the power function (2
πR
/
λ
)
4
. This rapid increase in scattering “efficiency” reaches a maximum when
R
/
λ
≈ 6.3/2
π
≈ 1. Recall that the Rayleigh scattering formula was derived assuming
R
/
λ
is small. For large enough particles the electric field within it is no longer approximately uniform, and this detracts from the cumulative effect for smaller ones, leading to a dramatic decline in
C
s
. The subsequent oscillatory behavior is a consequence of the particle size periodically meeting the requirements for destructive and constructive interference of the electric field within it.
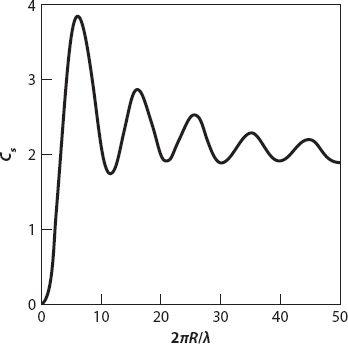
Figure 20.7. Dependence of the coefficient
C
s
on the ratio 2
πR
/
λ
for a spherical particle with refractive index equal to that of water, that is, ≈ 4/3. (The incident light is assumed to be monochromatic for simplicity.) Redrawn from Williamson (1973).
Consider the graph on the left side of the first maximum, say 0 < 2π
R
/
λ
< 4
π
≈ 12.6, and suppose that
R
is
fixed
. Then for longer wavelengths, corresponding to orange or red light, the scattering (as measured by
C
s
) is less than for shorter wavelengths, such as in blue or violet light, for that size particle (because
C
s
increases as
R
/
λ
increases). Now we let
R
be a somewhat larger (but still fixed) value corresponding to the decreasing part of the graph after the first maximum. This time the scattering efficiency is reversed:
C
s
decreases as
λ
decreases. It should be apparent that, given a suitable size distribution of particles—such as those from forest fires or volcanic eruptions—the sun or moon may appear strangely colored—blue moons and even green ones have been reported [
36
].
While the amount of light scattered by a particle is of theoretical interest, the amount scattered by a given mass concentration of particles is of more direct interest in gauging the effects of air pollution. For simplicity, we consider the particles to be of uniform size and density
ρ
. Then the mass of each particle is
m
= 4
πρR
/
3
. If
M
is the particle mass concentration (the mass of pollutant per unit volume, for example,
c
mg/m
3
), then a cylinder of cross-sectional area 1 m
2
will contain
M
/
m
= 3
M
/4
πρR
3
particles for every meter of its length. Multiplying this number by the effective particle cross-sectional area
C
s
πR
2
gives a relative measure of the amount
f
of the incident beam that is scattered, that is,
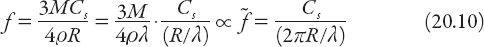
for a given wavelength of light.
Figure 20.8
shows a graph of this ratio denoted by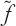 ; valid for any prescribed wavelength, it shows how scattering of light for a given mass concentration is most efficient when the wavelength of light is close to the particle size, that is,
; valid for any prescribed wavelength, it shows how scattering of light for a given mass concentration is most efficient when the wavelength of light is close to the particle size, that is,
λ
≈
R
.
