X and the City: Modeling Aspects of Urban Life (65 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

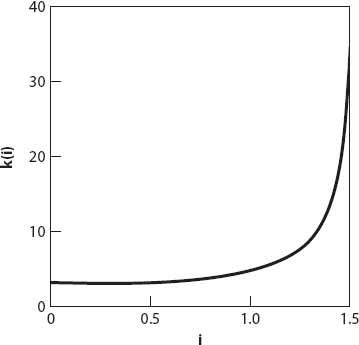
Figure 21.6. The function
k(i)
in equation (21.6).
There are two additional factors that can modify the approximation (21.6), one being due to the divergence of the rays from a light source which is in practice
not
infinitely far away (and neither is the observer!). Suppose that the light source
L
is a distance
R
L
from the glass, the distance of the observer
O
is
R
O
, and the distance between these two points on the glass is
d
. Using simple geometrical optics for a single ray from the light source
L
to the observer’s eye at
O
(via the point
P
on the glass surface) we can show that (
Figure 21.7
)
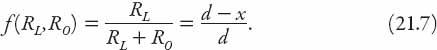
The factor
f
is basically a measure of the angle of incidence for an individual surface-reflected ray as determined by the relative positions of source and observer (and is independent of the earlier geometric argument leading to equation (21.6)). It approaches one as the distance of the light from the glass (relative to the observer) becomes larger. Conversely, as this relative distance becomes smaller,
f
decreases toward zero. The factors
k
and
f
in equations (21.6) and (21.7), respectively, will tend to counteract one another as the angle of incidence approaches 90°.
Another geometric factor (cos ) comes from when the plane of incidence (containing the incident and reflected rays) is at an angle
) comes from when the plane of incidence (containing the incident and reflected rays) is at an angle to the plane containing the wedge angle of the glass (i.e., the plane is rotated by an angle
to the plane containing the wedge angle of the glass (i.e., the plane is rotated by an angle about the normal to the glass pane). This factor will reduce the angular distance between the two images unless
about the normal to the glass pane). This factor will reduce the angular distance between the two images unless = 90°. Taking all these factors into consideration, we have the more general approximation for
= 90°. Taking all these factors into consideration, we have the more general approximation for
δi
, namely
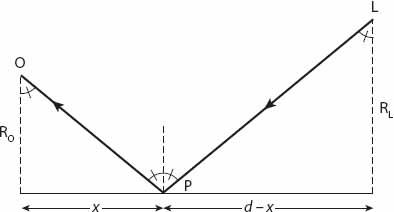
Figure 21.7. The basic observer (
O
)-light source (
L
) geometry, neglecting the effects of wedge refraction for the additional factor f in equation (21.7).
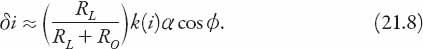
=
r
(
t
) : RAIN “SPARKS”
After it has been raining a while and there are several large puddles on the road, as you walk you may notice that the light’s reflection is surrounded by momentary “sparks” emanating from where the raindrops hit the surface. They appear to point radially outward. In his classic book
Light and Colour in the Open Air
, Marcel Minnaert [
38
] points out that “the explanation is simple.” Let’s see. When a drop hits the surface of the water it generates a set of concentric circular wave patterns (see
Chapter 25
for more details about this). As the wave with center
C
expands (see
Figure 21.8
), a sequence of reflections occurs in an almost continuous fashion along the line
CM
(
C
1
and
C
2
are intermediate points of reflection). As the wave expands outward, so does the point of reflection, giving the appearance of rapidly moving sparks of light.
A related reflection phenomenon occurs when a street lamp is observed through the crown of a tree (
Figure 21.9a
). The light is reflected into the observer’s eyes by twigs and leaves, and the effect is enhanced if the tree is wet after rain, or even frost-covered. As indicated in
Figure 21.9a
, all the branches and twigs in a given plane may contribute reflections to the observer, but those parallel to the line EL will be greatly foreshortened compared with those perpendicular to that line. Those between these orientations will be foreshortened proportionately less. As such, the combined effect will be to create a “halo” effect—a set of approximately concentric circles (or arcs of such circles).
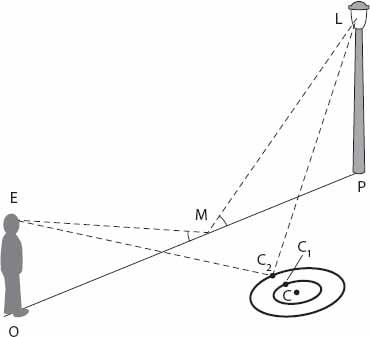
Figure 21.8. “Rain spark” geometry.
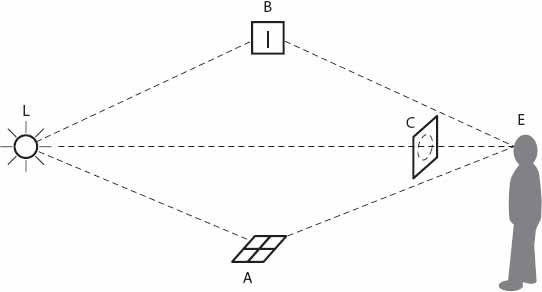
Figure 21.9a. “Rain circle” geometry when a source of light shines through wet leaves and twigs.
