X and the City: Modeling Aspects of Urban Life (72 page)

This can be rearranged as

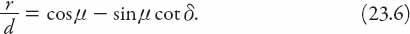
From
Figure 23.8
it is apparent that

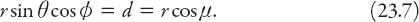
By substituting for
μ
from equation (23.7) into (23.6) we obtain the following expression for the relative distance
R
of the rainbow slice along the beam, where
R
=
r
/
d
:

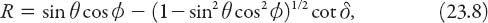
noting again that
δ
≈ 138° for the primary bow. The polar graphs for
R
are qualitatively similar to those for the lighthouse beam in
Figure 23.4
, and will not be reproduced here. Again, “virtual” loops can appear in the plots if the angle
θ
is too large, corresponding the bow disappearing for a small range of the
on the far side of the beam (see Harsch and Walker (1975)). This does not occur for
θ
< 48° approximately, as may be verified by setting
R
= 0 and
= 180° in equation (23.8). The analysis for a secondary rainbow is of course very similar, but also will not be repeated here.

There is an interesting optical illusion associated with a rotating lighthouse beam. The beam appears to change its length in a continuous fashion, attaining its maximum length when passing overhead, and reaching its minimum when the beam is pointing directly away from the observer. To understand why this is so, let’s visit a star party.

Have you ever used a flashlight beam as a pointer to identify particular stars, star groups, or planets to interested bystanders? Perhaps there were none. No matter; you may have noticed that even if the sky is clear, the beam seems to come to an end very abruptly in a particular direction. But why do we see the beam in the first place? The explanation is the same as that for the visibility of sunbeams: dust particles and water droplets in the beam scatter the light, some of which of course enters the eyes of the observer. In
Figure 23.9
, the observer—you—is at the point
O
and the beam of light starts at
L
and extends (while diverging somewhat) to
C
and beyond. From points
A
,
B
,
C
, etc. in the forward direction, light is scattered toward the observer, but no matter how much the beam extends, the observer, displaced from it, will never see it extend beyond the direction
OD
(parallel to the axis of symmetry of the beam). When such a beam is rotating, the apparent length will change in accordance with the angle the beam makes with the observer-source line.

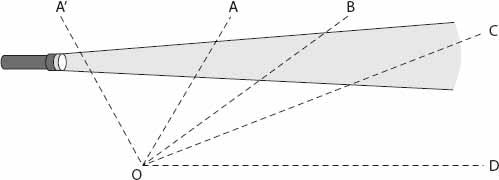
Figure 23.9. Geometry of the flashlight beam. The observer is at
O
. The point L (not shown) is where the beam begins.

But why can we see a lighthouse beam anyway? Or a flashlight beam, for that matter? The answers may seem obvious; it’s all about photons entering our eyes, isn’t it? Well, yes (always) and no! If a flashlight is shone directly into our eyes, we have no choice but to see it, unless we close our eyes. But if it is pointed away from us, we can usually still see it. The closer the direction of sight is to that direction, the wider the beam is, and the more scattering particles there are, and this will to some extent counteract the fact that the beam is more remote from
O
in that direction. However, if you look in the direction
OA
′ and compare the intensity of scattered light with that when you look in the direction
OA
(roughly 90° from
OA
′), you will notice that the former is considerably greater: more light is scattered in the forward direction than in the backward one. The very same phenomenon occur with lighthouse beams—a beam pointing toward the observer is brighter than when it points away from him.

As we noted in more detail in
Chapter 20
, the explanation is that the particles scattering the light are sufficiently large that they scatter asymmetrically: much more light is scattered in the forward direction. This is (in case you had forgotten) essentially why the color of the blue sky can change as a result of changing proportions of dust, ash, salt particles, and water droplets in the atmosphere, and it also accounts for some of the differences between a blue sky in southern Europe, or the tropics, and a blue sky (when it occurs!) in northern England. Basically, small particles (of size ≈ 10
⁻⁸
m) scatter blue and violet light most, and with almost equal intensity in all directions, whereas large particles (of size ≈ 10
⁻⁶
m) scatter all colors more or less equally, but mostly at small scattering angles (i.e., in the forward direction).

Some final comments can be made to wrap things up in this chapter. We have discussed rainbow and halo slices in lighthouse and searchlight beams, but can we really see the rainbow colors in these cases? Generally, it seems unlikely for several reasons, one being that the human eye is less sensitive to color at low light intensities, as evidenced by the contrast between rainbows and halos produced in moonlight as opposed to sunlight. Perhaps a more substantial reason is that modern lighthouses use sodium or mercury-vapor lights (which are “nearly” monochromatic) or incandescent bulbs, though light from the latter can exhibit a reddish tinge sufficiently far from the source—for reasons the reader should be able to infer by now!

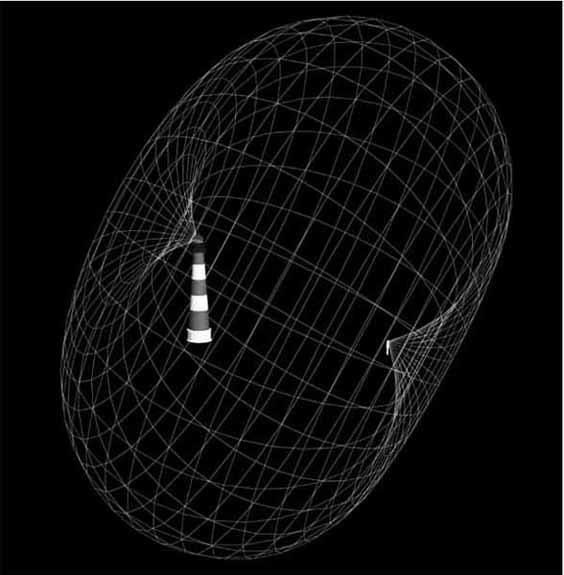
Figure 23.10. “Minnaert cigar” for a lighthouse beam. Compare the surface near the light with the shape of the rainbow arc in
Figure 23.1
. Courtesy of Achim Christopher.

Lighthouse beams are generally quite divergent, unlike the more collimated versions implied by the figures above. How does this affect the conclusions we
have drawn on the basis of some rather interesting trigonometry? Instead of “slices,” the rainbows (or at least, the brighter portions of the beam) will take the shape of part of the (appropriate) curve shown in
Figure 23.5
. This is beautifully illustrated in
Figure 23.2
. The corresponding apple-shaped “Minnaert cigar” that we have discussed in
Chapter 22
is illustrated in
Figure 23.10
.