X and the City: Modeling Aspects of Urban Life (84 page)

In the sun, the corresponding path length is about 1 mm, not 1 foot. This is the average distance light travels before being absorbed, based on estimates of the density and temperature inside the sun. The radius of the sun is about 700,000 km, or 7 × 10
⁵
km, or approximately 10
¹²
mm, rounding up for simplicity to the nearest power of ten. Now watch carefully: there’s nothing up my sleeve. We require this distance, the radius of the sun, to be the value of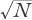
, the distance from the center traveled by our randomly “walking” photon. This means that
N
≈ (10
¹²
)
²
= 10
²⁴
, and 10
²⁴
mm steps is 10
¹⁸
km. Now 1 light year is about 10
¹³
km (check it for yourself!), so
N
≈ 10
⁵
light years, which by definition takes 10
⁵
or 100,000 years! Good gracious me!

Now we formulate the one-dimensional diffusion equation in a very similar fashion. Basically, we wish to be able to describe the “density” of a distribution of “particles” along a straight line (the
x
-direction) as a function of time (
t
).
N
(
x
,
t
) will denote the density of particles (number per unit volume) at location
x
and time
t
. How many particles at time
t
will move across unit area perpendicular to the
x
-direction from
x
to
x
+
δx
? By the time
t
+
τ
(i.e., during the next time step), half of the particles will have moved to the location
x
+
δ
and half of those located at
x
+
δ
will have moved to
x
(see
Figure A10.1
). This means that the net number moving from
x
to
x
+
δx
is [
N
(
x,t
) −
N
(
x
+
δ
,
t
)]/2. The total number of these particles per unit time and per unit area is called the
net flux
. We’ll call this
F
_x
and rearrange it as

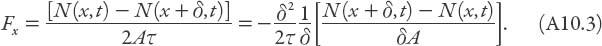
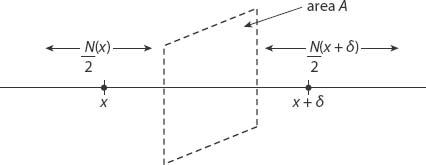
Figure A10.1. Schematic for the flux argument leading to equation (A10.4).

The quantity
δ
²
/2
τ
has dimensions of (distance)
²
/(time), and this will be called the
diffusion coefficient D
. The first quotient in square brackets is the number of particles per unit volume at
x
+
δ
and time
t
. This is just the concentration, denoted by
C
(
x
+
δ
,
t
). Similarly, the second term is
C
(
x
,
t
). This means that we can rewrite the net flux as

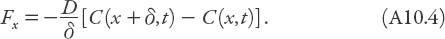
At this point we are in a position to carry out a familiar procedure: taking the limit of this quotient as
δ
→ 0. If this limit exists, we can write

Physically this means that the net flux is proportional to the concentration gradient, and it moves in the opposite direction. We can think of it this by imagining instead that
C
is temperature; the flow of heat will be from the higher temperature region toward the lower one—in a direction opposite to the gradient of the temperature. If on the other hand
C
is the concentration of sugar in my tea, the flow of sugar molecules is toward regions of lower concentration.

Let’s take this one stage farther and consider a little slab of thickness
δ
and area
A
perpendicular to the
x
-axis (see
Figure A10.2
). In a time
τ
, the number of particles entering from the left is
F
_x
(
x
)
Aτ
, while
F
_x
(
x
+
δ
)
Aτ
leave from the right (assuming no particles are created or destroyed). This means that the number of particles per unit volume in the slab must increase at a rate given by the expression

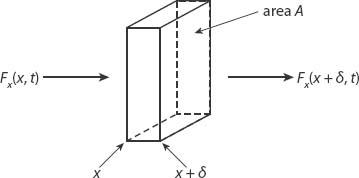
Figure A10.2. Schematic for the flux argument leading to equation (A10.6).

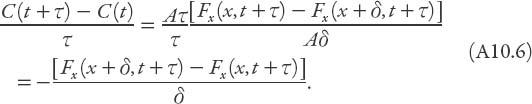
In the limit
τ
→ 0,
δ
→ 0 we obtain

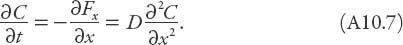
There is another mechanism that must be included in any realistic discussion of pollution: wind. As with the discussion in
Chapter 19
we shall consider the effects of a wind with constant speed
U
in the
x
-direction only (even when a higher-dimensional diffusion equation is used). The rate at which particles enter the slab per unit volume is approximately
UC
(
x
,
t
)
A
, so the wind’s contribution to the right-hand side of the diffusion equation is approximately