X and the City: Modeling Aspects of Urban Life (86 page)

Halos are formed when sunlight is refracted, reflected, or both from ice crystals in the upper atmosphere and enters the eye of a careful observer: be careful, because even the common types are easily missed (but never look directly at the sun, of course). As already noted, they are often produced when a thin uniform layer of cirrus or cirrostratus cloud covers large portions of the sky, especially in the vicinity of the sun. Surprisingly, perhaps, they may occur
at any time of the year, even during high summer, because above an altitude of about 10 km it is always cold enough for ice crystals to form. In particularly cold climes, of course, such crystals can form at ground level (though we are not thinking here of snow crystals). Such halos can arise from
diamond dust
, which is essentially ground-level cloud composed of tiny ice crystals. It can form wherever the temperature is well below freezing. Of course, some types of halo (such as a
circumhorizontal arc
) are very latitude-dependent, and may therefore be seen only rarely in higher latitudes. Very many of the crystals producing halos are hexagonal prisms; some are thin flat plates while others are long columns, and sometimes the latter have bullet-like or pencil-like ends. A significant feature of all these crystals is that while any given type may have a range of sizes, the angles between the faces are the same. Although they do not possess perfect hexagonal symmetry, of course, they are sufficiently close to this that simple geometry based on such idealized forms suffices to describe the many different arcs and halos that are seen. The halos that result from cirrus cloud crystals depend on two major factors: their shape and their orientation as they fall. Their shape is determined to a great extent by their history, that is, the temperature of the regions through which they drift as they are drawn down by gravity and buffeted around by winds and convection currents.

In order to explain the reasons for the various angles, for example, 22°, it is necessary to examine the crystal geometry in more detail. It is clear from
Figure A11.2
that hexagonal ice crystals can be thought of as presenting “prism angles” of 60°, 90°, or 120° to rays entering them in the planes indicated, depending on the orientation of the crystal. There are both similarities and differences with the formation of rainbows in raindrops, and noting that a sphere is (infinitely) more symmetrical than a regular hexagonal plate, a result from optics that is extremely important for such halos is
that the deviation angle for light refracted through a prism is a minimum for symmetric ray paths
.

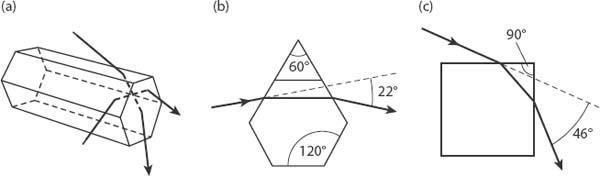
Figure A11.2. Ray paths through hexagonal ice crystal prisms for both the 22° and the rarer 46° halos.

Recall that a rainbow arises when the angle through which a ray is deviated on passing through the raindrop is an extremum. The above result tells us that in the case of prisms, the corresponding extremum—also a minimum, in fact—occurs when the ray path through the crystal is symmetric. A second result from elementary optics defines the magnitude of this minimum deviation angle (
D
_m
)—the location of the halo relative to the line joining the sun and the observer—in terms of the refractive index (of ice here) and the apex angle of the prism.

We can use these results to explain the occurrence of the 22° and the less common 46° halos. As shown in
Figure A11.2
(
b,c
), there are three prism angles in a hexagonal ice crystal prism: 60° (light entering side 1 and exiting side 3); 90° (light entering a top or bottom face and exiting through a side) and 120° (light entering side 1 and being totally internally reflected by side 2). The first two of these create color by dispersion of sunlight; the last contributes nothing directly to a halo, at least of interest to us here. The refractive index of ice for yellow light is
n
≈ 1.31 For an apex angle of 60°,
D
_m
≈ 22°, and for an apex angle of 90°,
D
_m
≈ 46°. As in the case of the rainbow, all possible deviations are present in reality, but it is the “clustering” of deviated rays near the minimum that provides the observed intensity in the halos (but unlike the case of the rainbow, no reflection contributes to their formation in these two cases).

How effective is the Earth at clearing a path through “space matter” in its vicinity? This is of interest, of course, with regard to possible close encounters with asteroids, as discussed in
Chapter 24
. In order to get a handle on this problem, one major task is to determine how effective the Earth is at capturing “errant” asteroids. In order to do so, we will use some elementary physical principles and properties of conic sections.

Because of the gravitational attraction of the Earth (or any other sufficiently massive body), it can in principle “pull in” objects that are not traveling directly toward a head-on collision. This results in a
capture cross section
(CCS) that is at least as large as its
geometric cross section
(GCS). It is clear that this will depend (in particular) on the speed of the object relative to the Earth; something “whizzing by” our planet at high speed is less likely to be captured than a much slower object on the same path.

We can reduce this to a simple “two-body” problem by ignoring, for now, the rest of universe (as I so often do). The approach here is based on the article by Tatum (1997) [
47
]. Essentially, we consider the trajectory of the asteroid to be such that the gravitational attraction of the Earth is the dominant mechanism in this encounter. This is reasonable since the force of attraction of the Earth is ten times that of the sun at a distance of about 52,000 miles, or 13 Earth radii from its center, and about 1700 times that of the moon at this same distance. Under this assumption we can regard the trajectory of the asteroid as a hyperbolic one about a stationary Earth. Of course, both objects are in elliptical orbits around the sun, but in this “geocentric model” a hyperbolic orbit around the Earth is perfectly adequate for a “back of the envelope” calculation such as this.

The notation is as follows (see
Figure A12.1
). The impact parameter
B
(no pun intended) is the closest distance of approach to Earth’s center that the asteroid would have it were on a straight line path, that is, one unaffected by
Earth’s gravitational attraction (or more accurately, by their mutual gravitational attraction). Its initial speed (at “infinity”) is
v
₀
and the equation of its hyperbolic path is

a
being the
x
-intercept and
b
the semi-transverse axis of the conjugate hyperbola.

Exercise:
Using
Figure A12.1
, show that the impact parameter

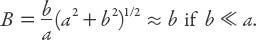
The closest distance of approach on the hyperbolic orbit is called the
perigee distance p
, and if
R
is the radius of the Earth, the asteroid will collide with the Earth if
p
<
R
(the case
p
=
R
corresponds to grazing incidence). The GCS of the Earth is
πR
²
and the potential CCS is defined to be
πB
²
. How do these two areas compare as a function of the initial speed
v
₀
?

First we will need to calculate the potential energy Φ(
) of the asteroid under the action of the Earth’s gravitational field, where
is the position vector of the asteroid relative to the Earth. The gravitational force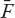
, described by the famous inverse-square law, is directed along the radius vector
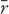joining the two bodies, and for a spherically symmetric force Φ is given by