X and the City: Modeling Aspects of Urban Life (83 page)

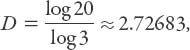
(intruding well into the third dimension). Now for
Cantor dust
: what is that? Take any line segment and remove the middle third; this is the basic iteration. In the limit of an infinity of such iterations for which
a
= 1/3 and
N
= 2, it follows that

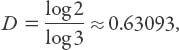
which is obviously less than one. Quite amazing.

Consider the motion of non-interacting “point particles” along the
x
-axis only, starting at time
t
= 0 and
x
= 0 and executing a
random walk
. The particles can be whatever we wish them to be: molecules, pollen, cars, inebriated people, white-tailed deer, rabbits, viruses, or anything else as long as there are sufficiently many for us to be able to assume a continuous distribution, and yet not so dense that they interact and interfere with one another (though this may seem rather like “having our cake and eating it”!). In its simplest description the particle motion is subject to the following constraints or “rules”:

1. Every
τ
seconds, each particle moves to the left or the right, moving at speed
v
, a distance
δ
= ±
vτ
. We consider all these parameters to be constants, but in reality they will depend on the size of the particle and the medium in which it moves.

2. The probability of a particle moving to the left is ½, and that of moving to the right is also ½. Thus they have no “memory” of previous steps (just like the toss of a fair coin); successive steps are statistically independent, so the walk is not biased.

3. As mentioned above, each particle moves independently of the others (valid if the density of particles in the medium is sufficiently dilute).

Some consequences of these assumptions are that (i) the particles go nowhere on the average and (ii) that their root-mean-square displacement is proportional, not to the time elapsed, but to the
square root
of the time elapsed. Let’s see why this is so. With
N
particles, suppose that the position of the
i
th particle after the
n
th step is denoted by
x
_i
(
n
). From rule 1 it follows that
x
_i
(
n
) −
x
_i
(
n
− 1) = ±
δ
. From rule 2, the + sign will apply to about half the particles
and the − sign will apply to the other half if
N
is sufficiently large; in practice this will be the case for molecules. Then the mean displacement of the particles after the
n
th step is

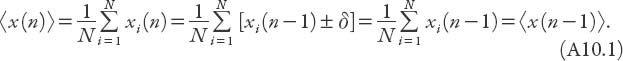
That is, the mean position does not change from step to step, and since they all started at the origin, the mean position is still the origin! This means that the spread of the particles is symmetric about the origin.

Let’s now consider the mean-square displacement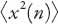
. It is clear that

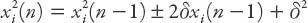
so that

Since
x
_i
(0) = 0 for all particles
i
,

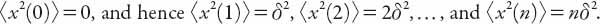
Thus the mean-square displacement increases as the step number
n
, and the root-mean-square displacement increases as the
square root
of the step number
n
. But the particles execute
n
steps in a time
t
=
nτ
so
n
is proportional to
t
. Thus the spreading is proportional to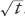
. And as we have shown in
Chapter 19
for the case of a time-independent smokestack plume or a line of traffic, the spreading is proportional, in the same fashion, to the square root of distance from the source.

Incidentally, there is a very nice application of these ideas, extended to three dimensions, in the book by Ehrlich (1993). In an essay entitled “How slow can light go?” he points out that, barring exotic places like neutron stars and black holes, it’s probably in the center of stars that light travels most slowly. This is because the denser the medium is, the slower is the speed of light.

In fact, it takes light generated in the central core of our star, the sun, about 100,000 years to reach the surface! (Do not confuse this with the 8.3 minutes
it takes for light to reach Earth from the sun’s surface.) The reason for this long time is that the sun is extremely opaque, especially in its deep interior. This means that light travels only a short distance (the
path length
) before being absorbed and re-emitted (usually in a different direction). The path of a typical photon of light traces out a
random walk
in three dimensions, much like the two-dimensional path of a highly inebriated person walking away from a lamppost. After a random walk consisting of
N
steps of length (say) 1 ft each, it would be very unlikely for the person to end up
N
feet away from the lamppost. In fact the average distance staggered away from the lamppost turns out to be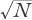
feet.