A Player's Guide to Chords and Harmony (19 page)

Figure 5-18. This progression is identical to the one in Figure 5-17, except that major 7th chords are used in place of the major triads in bars I and 3. The consistent use of 7th chords is more characteristic of the types of jazz where this sort of progression would be used.

We've already seen a few examples in which one chord was substituted for another (for example, the deceptive cadence shown in Chapter Four). Jazz musicians, however, have discovered and explored many ways of substituting one chord for another. Some will be discussed later in this book, and you may be able to learn others by listening or playing your instrument. One substitution that uses the dominant 7th is both simple enough and important enough to be worth explaining here.

Figure 5-19. This left-hand pattern is one of the staples of boogie-woogie piano, a bluesoriented style that was popular in the 1930s and 1940s. Boogie-woogie was one of the precursors of rock and roll. A dominant 7th chord is outlined by the root and 7th played on the third beat of each bar.

This substitution goes by several names. It can be called a flat-five substitution, an aug-four substitution, or a tritone substitution. Whatever you choose to call it, the idea is the same: In certain circumstances, a dominant 7th chord can be replaced with a different dominant 7th whose root is a tritone (an augmented 4th or diminished 5th) away from the root of the original chord.

Take a look at the two progressions in Figure 5-20. The first and third chords are identical, but in place of the expected dominant 7th chord in (a), I've substituted a D67 chord. D6 is an augmented 4th away from the original root, G. The same idea is used in Figure 5-21. This example is almost identical to Figure 5-15, where each dominant 7th (from E7 through D7) is a secondary dominant in relation to the following root. However, in Figure 5-21 the D7 chord has been replaced by an A67 The root of the A67 is an augmented 4th away from the root of D7.

Figure 5-20. In jazz, it's usually possible to replace a dominant 7th chord with another dominant 7th whose root is a tritone away from the original root. Here, a standard II-V-I progression is shown in (a). The progression in (b) is identical except that a D67 chord has been substituted for the G7.

Figure 5-21. Another tritone substitution. This progression is identical to the one in Figure 5-15, except that an A67 has been substituted for the D7.

THE CIRCLE OF FIFTHS

As Figure 5-15 shows, it's possible to string together a series of dominant 7th chords in which each chord is the dominant in relation to the root of the next chord. If we string together 12 chords in this manner, the chord roots will move through all 12 notes of the chromatic scale, and we'll find ourselves back where we started. Such a progression, which is shown in Figure 5-22, is not very satisfying, because it provides no clue about which note is the tonic. We seem to be entirely at sea.

Figure 5-22. Each dominant 7th chord in this progression is preceded by its own secondary dominant. The progression moves through all 12 roots in the chromatic scale without ever arriving at a resting place. (Note that F#7 is the enharmonic equivalent of G67. Technically, D67 is the dominant of G6, not of F#.)

The roots of the chords in Figure 5-22 are all separated from one another by an interval of a 5th. If we plot them on a circle (to show the endless nature of the progression), we'll have the classic diagram in Figure 5-23. This diagram is called the Circle of Fifths. Some people prefer the term "Cycle of Fifths.'

The Circle of Fifths is well worth studying and understanding. For one thing, it shows the arrangement of key signatures given in Chapter One. Each time we add a sharp to the key signature, or remove a flat, we move clockwise around the Circle of Fifths. For example, from C to G we add one sharp (F#), and from E6 to B6 we remove one flat (A6). Conversely, when moving counterclockwise around the Circle of Fifths, we remove one sharp from the key signature, or add one flat to it. For example, when the key changes from A to D we remove one sharp (G#).

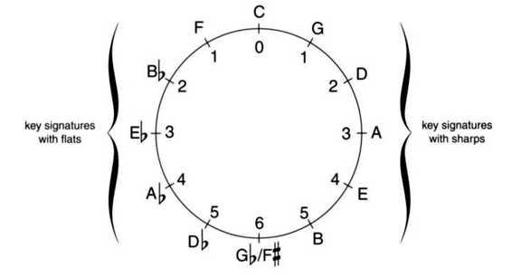
Figure 5-23. The Circle of Fifths. The numbers inside the circle refer to the number of flats (on the left) or sharps (on the right) in the major key signature.

The sharps and flats that are added to key signatures also follow the Circle. The new sharp added to a key signature on the right half of the Circle is always the note two steps counterclockwise from the key. The new sharp added to the key of A, for instance, is G#. The new flat added to a key signature with flats, on the other hand, is always the note one step counterclockwise. When moving from the key of F, for instance (whose only flat is B6) to the key of B6, we add an E6 to the key signature.

The notes directly opposite one another on the Circle are separated by the interval of a tritone. And both the notes in a diminished 7th chord and the notes in an augmented triad are easy to spot on the Circle, because the notes form regular geometrical shapes (a square and an equilateral triangle, respectively).

The roots of each IIm7 V7-I progression lie next to one another on the circle. For instance, if the first chord is a Bm7, we can find the next two by moving counterclockwise from B to E and then to A. The full progression would be Bm7-E7-A. This type of chord movement, counterclockwise around the Circle, is what jazz musicians refer to as "back-cycling"

7TH CHORD VOICINGS

Like the triads discussed in Chapter Three, 7th chords can be voiced in various ways. In fact, as the number of notes in the chord increases, the number of voicings available increases exponentially. A number of voicings of 7th chords have been used in the examples in this chapter, but most of them have been closed voicings. To learn to use 7th chords, you should spend a little time at the keyboard trying out alternate voicings, such as those shown in Figure 5-24.

Figure 5-24. A few ways, chosen more or less at random, in which 7th chords can be voiced.

You may have noticed that in some of the examples used earlier in this chapter, the 5th was omitted from 7th chord voicings. This is a very common practice. The 5th contributes less to the characteristic sound of a straight 7th chord (whether it's a dominant 7th, a minor 7th, or a major 7th). The root can't usually be omitted, because if it is the voicing becomes ambiguous, as shown in Figure 5-25. If the 7th is omitted, the chord becomes an ordinary triad. And if the 3rd is omitted, the listener has no way to determine whether the chord is major or minor - an important factor in figuring out the meaning of a particular chord or progression. So when it becomes desirable to lighten up a chord voicing by leaving something out, the 5th is the first note to go.

Figure 5-25. When the root is eliminated from a 7th chord, what remains is a triad with a different root. It's useful to take a look at the type of triad created by the upper three voices. In a V7 chord, for instance, the upper voices are the diminished triad built on the leading tone of the major scale. In an earlier chapter, we noted that this triad is seldom used by itself. When placed above a V root, however, it becomes extremely useful. The upper voices of other 7th chords form augmented, major, and minor triads, as shown. The upper voices of the 765 and 7#5 chords (see Figure 5-28) don't form functional triads.