Chances Are (10 page)

There was no doubt where science had to go to remain science: all facts were to be considered as mere probabilities, and all probabilities, frequencies of observations. As von Mises saw it, anything else was simply a kind of false consciousness.

Given this view of pure science, it is certainly hard to see how probability could be legitimately applied to juries, deliberative assemblies, or voting systems. For von Mises, probability had only three areas of legitimacy: games of chance, certain mass social phenomena like genetics and insurance, and thermodynamics (where, as we will see in Chapter 11, it would take the leading role).

“Dost thou think, because thou art virtuous, there shall be no more cakes and ale?” Like all puritans, within or without the sciences, von Mises was asking his audience to give up much of what they felt made life worthwhile. People go into science because they want to discover and explain all the things around us that seem so richly freighted with meaning. But how many of the interesting phenomena of life truly are “collectives”—what fascinating event can be said to repeat exactly and indefinitely? While Laplace's system glided over the crack between stating equally possible outcomes and assuming them in experiment, von Mises' straddled a crevasse when it assumed that the relative frequencies of observed events could indeed approach a limiting value. All might be revealed in the long run—but, as Keynes pointed out, in the long run we are all dead.

 

Trains of thought can sometimes seem exactly that; bright little worlds rattling through unknown and perhaps uninhabited darkness. It is the cliché tragedy of intellectual life to discover, far too late, that your own train got switched off the main line up a remote spur whose rusty rails and lumpy roadbed reveal all too clearly that it leads only to ghost towns. Sometimes, though, there is the excitement of approaching the metropolis on converging lines: other golden windows glide alongside with other travelers folding their newspapers or reaching for their coats, other children waving in welcome.

Lebesgue's measure theory and von Mises' idea of frequency were ideas that were already within view of one another. Between them, two further trains were advancing: one was the growing conviction among physicists that certain processes in thermodynamics and quantum mechanics had
only
a probabilistic meaning—that there was no mechanical, deterministic model by which they could be described or even imagined. The other was the great contemporary movement, which promised that of all of mathematics—all the rigor and complexity that, magically, seem to find so many parallels with the richness and beauty of life—could be founded on a few axioms linked by the rules of deductive logic. There was a palpable sense of approaching the terminus, where the many travelers could exchange stories—all in the same language.

This shared language was the notion of the
set,
introduced by Georg Cantor as a means of keeping the infinite in mind without having to think of infinite things or infinite processes. The definition of a set is intentionally as loose as possible: it is defined by its members. But membership can be generated by the most varied of rules: “numbers divisible by 5” determines a set; but so does “Dog; 17; Red.” It is possible to have an empty set: we can talk about the contents of the box even though there's nothing in it. We can subdivide a set into
subsets,
which will also be sets. We can combine sets into a
union,
which is also a set. We can define where two sets overlap; the overlap or
intersection
is also a set. We can have infinite sets (such as all the counting numbers). And we can imagine the collection of all subsets of a set—which is also a set.

What, you might feel yourself asking, are we actually talking about here? Nothing in particular—and that's the point. This is pure form; its aim is to support a logical system that governs every instance of the way we consider some things as distinct from other things. A set is simply a pair of mental brackets, isolating “this” from “not this”; we can put into those brackets whatever interests us. Just as Cantor's infinity can be put in a set and considered here and now, rather than endlessly and forever, von Mises' indefinite sequences of observations can constitute a set: the set of events of observing something. We can use the axioms by which we manipulate sets to manipulate collections of events. Most important, Lebesgue's concept of measure gives us a method for assigning a unique and complete value to a set, its subsets, and its elements—and these values behave the way we want probability values to behave.

Lines of thought, all coming together, all converging—so who better to effect the final union than a man who was born on a train? Andrei Nikolaevich Kolmogorov was a son any parent would be proud of, but neither parent ever saw him. His mother died in bearing him, on April 25, 1903, journeying from the Crimea to her family estate, having left behind his father, an agronomist of clerical origin. The newborn Kolmogorov was swept up from the whistle-stop town of Tambov by his maiden aunt. She created a special school for her talented nephew and his little friends; it had its own magazine in which the young Andrei published his first mathematical discovery at the age of five: that the sum of the first
n
odd numbers is equal to
n
²
, as we too discovered in Chapter 1.

What immediately struck people who met Kolmogorov was his mental liveliness. He remained interested in everything, from metallurgy to Pushkin, from the papacy to nude skiing. His dacha, an old manor house outside Moscow, re-created the estate school of his youth. Presided over by his old aunt and his old nanny, it had a large library and was always full of guests: students, colleagues, visiting scholars.

It has been said that it would be simpler to list the areas of mathematics to which Kolmogorov did
not
make a significant contribution than to describe the vast range of topics he did explore—in depth—in his more than seventy years of productive work. His genius was to connect: he took mathematical ideas, clarified their expression, and then used them to transform new fields. He worked on mathematical logic, linking the classical and intuitionist traditions; he worked on function-space theory, extending it to the mechanics of turbulence; he invented the field of algorithmic complexity, and, with characteristic verve, he hoicked up the tottery edifice of probability and slipped new foundations underneath.

The basic premise of his system was simple: the
probability
of an
event
is the same as the
measure
of a
set
. We can use a diagram to make this idea even clearer. Take a rectangle:

Let's say that everything that can happen in the system we're interested in—every possible observation—is represented by a point in this rectangle. The probability measure of the rectangle (which, for flat things like rectangles, is its area) is therefore 1, because we can be certain that any observation is represented within it. If we are interested in, say, the flip of a coin, our diagram will look like this:

Two possible states, with equal area, having no points in common. The chance of throwing an even number with one die? Three independent, mutually exclusive events, totaling half the area of our rectangle:

We can see that this model nicely represents a key aspect of probability: that the probability of any of two or more independent events happening is determined by adding the probabilities of each. What about events that are not independent (such as, for instance, the event
A
, that this explanation is clear—and
B
, that it is true)? They look like this:

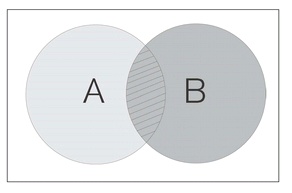
The probability that this explanation is
both
clear and true is represented by the area shared between
A
and
B
. The probability that it is
either
clear or true is represented by their combined area—although this is not the same as adding their individual areas, since then you would be counting their shared zone twice. The worrying probability that this explanation is
neither
clear nor true is represented by the bleak, empty remainder of the rectangle.

What about conditional probability—such as the probability this explanation is true
if
it is clear? We simply disregard everything outside the area of
A
(since we
presume
the explanation is clear) and compare its area with the area that it shares with
B
—which, as we know, represents clear
and
true.

You may find this all a bit simplistic, especially as someone who has come to it through the complex reasonings of Cardano, Pascal, de Moivre, Laplace, and von Mises. The point, though, is that this basic model can be scaled up to match the complexity of any situation, just as Euclid's axioms can generate all the forms needed to build Chartres cathedral. We need not think only of two circles; we can imagine hundreds, thousands, indeed an infinity of measurable subsets of our rectangular sample space, overlapping and interpenetrating like swirls of oil on water. Nor need our space be a two-dimensional rectangle; the same axioms would apply if our chosen measure were the volume of three-dimensional objects or the unvisualizable but mathematically conventional reality of
n
-dimensional space. And since this idea of probability borrows its structure from set theory, we can do logical, Boolean, calculations with it—well,
we
can't, but computers can, since they thrive on exactly those tweezer-and-mountain techniques of relentlessly iterated steps that fill human souls with despair.

There need be no special cases, cobbled-together rules or jury-rigged curves to cover this or that unusual situation. The point of Kolmogorov's work is that mathematical probability is not separate from the remainder of mathematics—it is simply an interesting aspect of measure theory with some quaint terminology handed down from its origins in real life.