Chances Are (9 page)
Authors: Michael Kaplan

Now let's assume the witness is mistaken: some other number came up and your life is wasted. This in itself has a probability of 2/3, which we multiply by the chance (1/2) that the witness is untruthful: our likelihood of discovering this as we trudge the path to Purgatory is therefore 2/3 Ã 1/2 = 1/3.
So we see that number 3 being drawn
and
hearing the truth about it is only half as likely as hearing that it was number 3 when it wasn't. We win only one-third of the timeâfar from Pascal's absolute certainty.
and
hearing the truth about it is only half as likely as hearing that it was number 3 when it wasn't. We win only one-third of the timeâfar from Pascal's absolute certainty.
We are back in the territory of the Blue Cab/Green Cab problem: when something is intrinsically rare or unlikely, it doesn't matter how truthful or sincere a witness isâthe essential unlikelihood prevails. Even if the witness were 90 percent accurate, the chance of being told accurately that you have won 1,000 happy lives is only 9 in 10,000. As the prize for the celestial lottery goes up, the odds of hearing truthfully that you have won it go downâeven without considering any multiplying factors for the self-interest of the witnesses.
Â
Laplace's calculus of probabilities was intended to give us a mechanism by which we could conquer error and see as on shining tablets the essential laws of the universe. Yet nowadays, we see it as applicable only to a degree and only to a few selected problems. How did this powerful paradigm come to grief? In part, it suffered from that which affects so many great and convincing ideas: its very success tempted people to apply it in realms for which it was ill adapted, sciences far removed from its native astronomy: chemistry, biology, the ever hoped-for social sciences. Here, phenomena did not necessarily fall neatly in a normal distribution around a “true” value. New patterns, new distributions appeared that required a new calculus.
One early example of the new curves made necessary by wider observations was named for Laplace's student, Poisson, a former law clerk who hoped to apply probability to evidence and testimony. Poisson identified a class of events that, like crime,
could
happen quite easily at any time, but in fact happen rarely. Almost anyone in the world, for instance, could call you on the telephone right nowâbut it's highly unlikely that a ring actually coincided with the moment your eye passed that dash. Quite a lot of human affairs turn out to be like this: the chance of being hit by a car in Rome on any one day is very small, although passing a lifetime there makes the likelihood of at least a bump quite high. You might have a real interest in knowing the relative likelihoods of being run into once, twice, or more times.
could
happen quite easily at any time, but in fact happen rarely. Almost anyone in the world, for instance, could call you on the telephone right nowâbut it's highly unlikely that a ring actually coincided with the moment your eye passed that dash. Quite a lot of human affairs turn out to be like this: the chance of being hit by a car in Rome on any one day is very small, although passing a lifetime there makes the likelihood of at least a bump quite high. You might have a real interest in knowing the relative likelihoods of being run into once, twice, or more times.
Poisson's distribution is most like real life in not supposing that we know the actual probability of an event in advance. We already “know” the probabilities attached to each side of a die; we “know” the laws that should govern our observation of a planet's path. We can therefore multiply that known probability by the number of trials to give us our probability distribution. But in real life, we may not have that information; all we have is the product of the multiplication: the number of things that actually happened.
Poisson's curve, more a steeple than a bell, plots this product of probability times number of trials for things that happen rarely but have many opportunities to happen. The classical case of a Poisson distribution, studied and presented by the Russian-Polish statistician Ladislaus Bortkiewicz, is the number of cavalry troopers kicked to death by horses in 14 corps of the German army between 1875 and 1894.
Here are the raw figures:
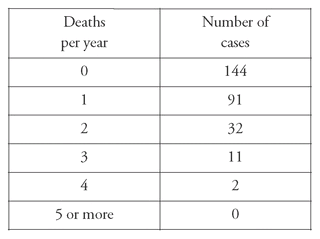
The total of trials (20 years x 14 corps) is 280; the total of deaths is 196; the figure for deaths per trial, therefore, is 0.7.
The Poisson formula for this would be
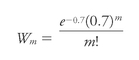 where
where
m
is the number of deaths per year whose probability we want to gauge. If
m
= 1, the probability is 0.3476. If this is applied to 280 experiments, the probable number of times one death would occur in any corps during one year is 97.3 (in fact, it was 91). The theoretical distribution is remarkably close to the actual one (which is probably why this is cited as the classical case):
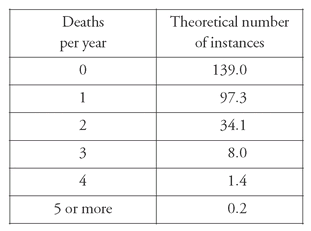
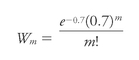
m
is the number of deaths per year whose probability we want to gauge. If
m
= 1, the probability is 0.3476. If this is applied to 280 experiments, the probable number of times one death would occur in any corps during one year is 97.3 (in fact, it was 91). The theoretical distribution is remarkably close to the actual one (which is probably why this is cited as the classical case):

If it happens you are not a cavalryman, what use could you make of this? Perhaps the best characterization of Poisson's distribution is that, whereas the normal distribution covers anticipated events, Poisson's covers events that are feared or hoped for (or both, as in the case of telephone calls). Supermarkets use it to predict the likelihood of running out of a given item on a given day; power companies the likelihood of a surge in demand. It also governed the chance that any one part of south London would be hit by a V2 rocket in 1944.
If you live in a large city, you might consider Poisson's distribution as governing your hope of meeting the love of your life. This suggests some interesting conclusions. Woody Allen pointed out that being bisexual doubles one's chance of a date on Saturday night; but sadly Poisson's curve shows very little change in response to even a doubling of innate probability, since that is still very small compared with the vast number of trials. Your chance of fulfillment remains dispiritingly low. Encouragingly, however, the greatest proportion of probability remains packed in the middle of the curve, implying that your best chance comes from seeking out and sustaining friendships with the people you already like most, rather than devoting too much time to the sad, the mad, or the bad alternative. Like staying away from the back ends of horses, this is a way to make the curve work for you.
Â
Poisson's distribution could be seen as a special case of the standard distributionâbut as probability advanced into statistics it came upon many more curves to conquer, if the mathematics and the data were to continue their engagement. Curves spiky, curves discontinuousâscatters that could not be called curves at all, although they were still defined by functions (that is, rules for assigning a single output to any given input). Mathematics spent much of the nineteenth century seeking methods to bind such boojums and snarks, snaring them in infinite series, caging them with compound constructions of tame sine-curves, snipping them into discrete lengths of manageabilityâgetting their measure.
At the turn of the century, the French mathematician Henri Lebesgue brought these many techniques to their philosophical conclusion: a way to assign a valueâa measureâto even the most savage of functions. Measure theory, as his creation was called, made it possible to rein in the wilder curves, gauging the probabilities they represented. It offered its power, though, at the price of intuition: a “measure” is just that. It is simply a means whereby one mathematical concept may be expressed in terms of another. It does not pretend to be a tool for understanding life.
By 1900 it was clear that if the counterintuitive need not be false, the intuitive need not be true. The classical approach to probability could no longer conceal its inherent problems. Laplace had founded his universal theory of probability on physical procedures like tossing a coin or rolling a die, because they had one particularly useful property: each outcome could be assumed to have equal probability. We know beforehand that a die will show six 1/6 of the time, and we can use this knowledge to build models of other, less well known, aspects of life. But think about this for a minute: how, actually,
do
we know these cases are equally probable?
do
we know these cases are equally probable?
Well, we could say we have no reason to believe they aren't; or that we must presuppose equal application of physical laws; or that this is an axiom of probability and we do not question it; or that if we didn't have equally probable cases . . . we'd have to
start all over again
, wouldn't we? All are arguments reflecting the comfortable, rational assumptions of Enlightenment scienceâand all draw the same sardonic, dismissive smile from our prosecutor, Richard von Mises.
start all over again
, wouldn't we? All are arguments reflecting the comfortable, rational assumptions of Enlightenment scienceâand all draw the same sardonic, dismissive smile from our prosecutor, Richard von Mises.
Â
Lemberg, alias Lwów, alias Lviv: a city that lies at the intersection of three sets in three dimensions: Polish, Austrian, Ukrainian; Catholic, Orthodox, Jewish; applied, abstract, artistic. It remains a symbol of intellectual promise for the debatable lands between the Vistula and the Dniepr; a Baroque lighthouse in a politicogeographic tempest. Its prominent sons and daughters would be themselves enough to populate a culture: the writers Martin Buber and Stanislaw Lem; the pianists Moriz Rosenthal and Emanuel Ax; the Ulam brothers, Stanislaw (mathematician) and Adam (historian); Doppler of the eponymous effect; Redl the spyânot to mention Weegee, Paul Muni, Sacher-Masoch, and the Muslim theologian Muhammad Asad (one of the few imams to be the son of a rabbi).
Lemberg's Richard von Mises was a pioneer in aerodynamics, designing and piloting in 1915 Austria-Hungary's monster bomber, the 600-horsepower Aviatik G. III. The plane was not a success, for many of the subtle local reasons that govern heavier-than-air flight. Perhaps in reaction, von Mises became increasingly interested in turbulence. Turbulence (as we will see later) lacks the pleasant predictability of the solar system; the swirls of fluid vortices may briefly resemble stately galaxies, but their true dynamics remain infuriatingly difficult to grasp. Von Mises was not an easygoing manâhe demanded of applied mathematics all the rigor of its pure cousinâand the more he worked in the unstable, fluttering world of flow, the less he liked the fixed but unexamined assumptions behind Laplace's idea of probability; defining it as “a number between 0 and 1, about which nothing else is known.”
The problem, von Mises thought, was that in assuming equally probable cases for our dice, coins, and urns, we had created out of nothing a parallel universe, in which things happened a certain way because they were
supposed
to. Instead of being messengers of the gods, the dice had become the gods. At best, the rules of probability were a tautology: the numbers 1 through 6 come up equally often in theory because we define them that way. At worst, the concept of equally probable cases prevented us from saying anything about what was before our eyes. What if the die has a few molecules missing from one corner, for instance? We have evidence, but no theorem based on equally probable cases applies to it; our probability calculus is irrelevant; we have to fall silent.
supposed
to. Instead of being messengers of the gods, the dice had become the gods. At best, the rules of probability were a tautology: the numbers 1 through 6 come up equally often in theory because we define them that way. At worst, the concept of equally probable cases prevented us from saying anything about what was before our eyes. What if the die has a few molecules missing from one corner, for instance? We have evidence, but no theorem based on equally probable cases applies to it; our probability calculus is irrelevant; we have to fall silent.
Von Mises' view was that the true reason for our believing that six should come up 1/6 of the time is no different from our reason for believing that the Earth takes 365.25 days to orbit the sun. That reason is our having
observed
it. “The probability of a six is a physical property of a given die”âa quantity derived from repeated experience, not some innate essence of creation or nature. Heads or tails, red or black, pass or no passâthese are no more phenomena in themselves than are grams, ohms, or pascals. Probability is a measure of certain aspects of consistent groups of events (“collectives,” in von Mises' terminology) revealed when these events are repeatable indefinitely.
observed
it. “The probability of a six is a physical property of a given die”âa quantity derived from repeated experience, not some innate essence of creation or nature. Heads or tails, red or black, pass or no passâthese are no more phenomena in themselves than are grams, ohms, or pascals. Probability is a measure of certain aspects of consistent groups of events (“collectives,” in von Mises' terminology) revealed when these events are repeatable indefinitely.
The nature of the “collective” has to be very particular: one must have a practically unlimited sequence of uniform but random observations. We can conclude that we have observed a given probability for a result if the relative frequency of that result approaches a limit, not just for the basic collective, but for randomly selected and mixed subgroups of the collective. The probabilities of combinations of results (like throwing two dice or taking two balls at a time out of an urn) can also be defined by keeping careful track of the order and subgroups of observations. That means that, while rigorously banishing any preconceptions of probability from our mind, we can gradually rebuild many aspects of its calculusâas long as we insist on describing frequencies, and restrict our observations to true collectives.
Other books
Tell Me It's Real by TJ Klune
Book of One 04: A Child of Fire by Baker, Jordan
Sudden--At Bay (A Sudden Western #2) by Frederick H. Christian
1972 - You're Dead Without Money by James Hadley Chase
Steam Guardians 01 - A Lady Can Never Be Too Curious by Mary Wine
Crossing the Line by Sherri Hayes
Conduct Unbecoming by Sinclair, Georgia
Miss Bangkok: Memoirs of a Thai Prostitute by Bua Boonmee
The Ultimate Egoist by Theodore Sturgeon
Bloody Kisses by Nelson, Virginia, DeWylde, Saranna, Royce, Rebecca, Breck, Alyssa, Proserpina, Ripley
