Chances Are (6 page)
Authors: Michael Kaplan

What do we have here? It seems, at first glance, to be no more than the sort of doodle found in the margins of all schoolbooks. Look at it more closely, thoughâas Pascal did in his
Traité du triangle arithmétique
âand you will see wonders of pattern. Let's start by skewing our triangle slightly, to make its rows, columns, and diagonals a little more clear.
Traité du triangle arithmétique
âand you will see wonders of pattern. Let's start by skewing our triangle slightly, to make its rows, columns, and diagonals a little more clear.

Pattern reveals itself first as a lesson in counting. The left column counts as infants do: “This one and then this one and then this one”; the second as grownups do, adding up as we go. The third column lists what are called
triangular numbers
, that is, the numbers of dots needed to construct equilateral triangles like these:
 (or the number of figures, row by row, in Pascal's own triangle: 1, 3, 6, 10 . . . see?). The next column lists
(or the number of figures, row by row, in Pascal's own triangle: 1, 3, 6, 10 . . . see?). The next column lists
pyramidal numbers
, the number of equal-size stones needed to build a regular pyramid with a triangular baseâand so on through Fibonacci series, fractal patterns, and further delights of complexity.
triangular numbers
, that is, the numbers of dots needed to construct equilateral triangles like these:

pyramidal numbers
, the number of equal-size stones needed to build a regular pyramid with a triangular baseâand so on through Fibonacci series, fractal patterns, and further delights of complexity.
The second trick of the triangle may have been discovered by the ancient Hindus and Chinese, and was certainly known to Omar Khayyám (an excellent mathematician as well as poet, tentmaker, and philosophical toper). You will probably remember from school how easy it is, when squaring a binomial (
a
+
b
), to forget to include all the relevant combinations in your multiplication: (2 + 3)
2
does not equal 2
2
+ 3
2
and so (
a
+
b
)
2
cannot equal
a
2
+
b
2
; instead, it equals:
a
+
b
), to forget to include all the relevant combinations in your multiplication: (2 + 3)
2
does not equal 2
2
+ 3
2
and so (
a
+
b
)
2
cannot equal
a
2
+
b
2
; instead, it equals:
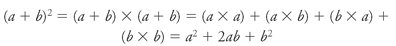
To calculate (
a
+
b
)
3
, and so on, you would need to include yet more combinations of terms:
a
+
b
)
3
, and so on, you would need to include yet more combinations of terms:
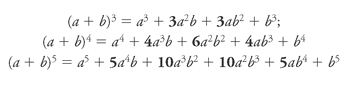
Does anything about the numbers in boldâthe binomial coefficientsâlook familiar? Yes, indeed. If you want to know the coefficient of any term in the expanded form of (
a
+
b
)
n
, simply count down
n
rows in Pascal's triangle (taking that first 1 you drew as row 0) and count across.
a
+
b
)
n
, simply count down
n
rows in Pascal's triangle (taking that first 1 you drew as row 0) and count across.
This is a pleasant discovery, but why does it work? Because, in multiplying out your binomial, you have to multiply each term by all the others and then sort the results into groups. In the expansion of (
a
+
b
)
5
, how many groups with 5
a'
s are there? One; but there are five groups with 4
a'
s and 1
b
and ten with 3
a'
s and 2
b'
s. So the coefficients tell you how many combinations of
a
and
b
you can make when you take them in groups of 1, 2, 3, or more.
a
+
b
)
5
, how many groups with 5
a'
s are there? One; but there are five groups with 4
a'
s and 1
b
and ten with 3
a'
s and 2
b'
s. So the coefficients tell you how many combinations of
a
and
b
you can make when you take them in groups of 1, 2, 3, or more.
We are now nearly ready to return to the gaming table and claim our share of the winnings. Play has stopped at a point where you are
r
points short of victory and your opponent
s
points short. If you were to go on with neither player gaining an advantage, the longest that play could continue would be another
r
+
s
â1 plays, since those are all the points available before one of you must win. Let's call this largest number of plays
n
. Now, on each one of these
n
attempts, you could win or your opponent could win; so the universe of all possible plays can be represented as (1 + 1)
n
: your potential point and your opponent's potential point through your
n
remaining potential games. Given that your opponent had
s
points to make when the game is interrupted, how much of that universe of 2
n
potential points is rightfully yours?
r
points short of victory and your opponent
s
points short. If you were to go on with neither player gaining an advantage, the longest that play could continue would be another
r
+
s
â1 plays, since those are all the points available before one of you must win. Let's call this largest number of plays
n
. Now, on each one of these
n
attempts, you could win or your opponent could win; so the universe of all possible plays can be represented as (1 + 1)
n
: your potential point and your opponent's potential point through your
n
remaining potential games. Given that your opponent had
s
points to make when the game is interrupted, how much of that universe of 2
n
potential points is rightfully yours?
(1 + 1)
n
has a familiar form: it's a binomial. So if we count
n
rows down Pascal's triangle (again, taking the top row as zero), we should find its expansion. And since
a
and
b
in this case both equal 1, the only significant terms in that expansion will be the binomial coefficients.
n
has a familiar form: it's a binomial. So if we count
n
rows down Pascal's triangle (again, taking the top row as zero), we should find its expansion. And since
a
and
b
in this case both equal 1, the only significant terms in that expansion will be the binomial coefficients.

The first term in the row is 1; this represents the single case in which you win all remaining points and the Venetian wins nothing; the second term represents the
n
cases in which you win all but one of the remaining points and your opponent wins one. Add this term to your total and go on, counting across and adding the coefficients until you get to the
s
th term of the expansion. From here on to the end, the territory belongs to your opponent: the coefficients represent the number of different ways he can win starting with
s
points to go. This is your point of division; by comparing the sum of the total number of ways you could have won with the total universe of points, 2
n
, you get the proportion for dividing the stakes.
n
cases in which you win all but one of the remaining points and your opponent wins one. Add this term to your total and go on, counting across and adding the coefficients until you get to the
s
th term of the expansion. From here on to the end, the territory belongs to your opponent: the coefficients represent the number of different ways he can win starting with
s
points to go. This is your point of division; by comparing the sum of the total number of ways you could have won with the total universe of points, 2
n
, you get the proportion for dividing the stakes.
Returning to the Venetian, still waiting impatiently: you were within 1 point of winning, but he needed 3. Therefore,
s
= 3. The total number of points that could be played (
n
) is 1 + 3 - 1 = 3. The universe of points is therefore 2
3
= 8. If you count down to the third row of the triangle, you find four coefficients: 1, 3, 3, 1. Since
s
= 3, you can add the first three coefficients to your total: 1 + 3 + 3 = 7. Compare this with the total universe of points, 8, and you find you have the right to 7/8 of the stakes, or 56 of the 64
pistolesâ
just as you found before.
s
= 3. The total number of points that could be played (
n
) is 1 + 3 - 1 = 3. The universe of points is therefore 2
3
= 8. If you count down to the third row of the triangle, you find four coefficients: 1, 3, 3, 1. Since
s
= 3, you can add the first three coefficients to your total: 1 + 3 + 3 = 7. Compare this with the total universe of points, 8, and you find you have the right to 7/8 of the stakes, or 56 of the 64
pistolesâ
just as you found before.
In 1654, the same year that God approached him in the form of fire, Pascal listed his accomplishments in a memorial to the Academy in Paris:
Â
... the uncertainty of fortune is so restrained by the equity of reason, that each of two players can always be assigned exactly what is rightly due. . . . By thus uniting the demonstrations of mathematics to the uncertainty of chance . . . it can take its name from both sides, and rightly claim the astonishing title: the geometry of chance.
Â
The
geometry
of chance: the same geometry Descartes had made interchangeable with equations. The spell of Pascal's triangle is not just in its elegant array of numerals: each line, if plotted as values on a graph, describes a shape; and successive lines describe that shape with greater and greater precision.
geometry
of chance: the same geometry Descartes had made interchangeable with equations. The spell of Pascal's triangle is not just in its elegant array of numerals: each line, if plotted as values on a graph, describes a shape; and successive lines describe that shape with greater and greater precision.

It is this shape that now governs our lives, that defines our normality: the normal, or standard, distributionâthe bell curve. The bell curve? How does this come from dicing with Venetians? Because the game we were playing was much more important than it seemed. Winning and losing is not simply a pastime; it is the model science uses to explore the universe. Flipping a coin or rolling a die is really asking a question: success or failure can be defined as getting a yes or no. So the distribution of probabilities in a game of chance is the same as that in any repeated testâeven though the result of any one test is unpredictable. The sum of all the numbers on the
n
th row of the triangle, 2
n
, is also the total of possible answers to a yes-or-no question asked
n
times. The binomial coefficients, read across the row, count the number of ways either answer can appear, from
n
yeses to
n
nos. If, as here, a perfect bell curve arises from your repeated questioning, you will know that the matter, like Pascal's game, involves a 50-50 chance.
n
th row of the triangle, 2
n
, is also the total of possible answers to a yes-or-no question asked
n
times. The binomial coefficients, read across the row, count the number of ways either answer can appear, from
n
yeses to
n
nos. If, as here, a perfect bell curve arises from your repeated questioning, you will know that the matter, like Pascal's game, involves a 50-50 chance.
A game, though, must have rules. How can we try our skill or strength against each other if every trial is different? This is the secret weakness of the method Pascal revealed: we must show we were always playing the same game for the scores to count. That's a straightforward task as long as we stay with dice and coinsâbut as questions become deeper, it grows ever harder to prove that test
n
is truly identical to test 1. Think, for instance, of asking the same person
n
times the most significant yes-or-no question of all: “Do you love me?”
n
is truly identical to test 1. Think, for instance, of asking the same person
n
times the most significant yes-or-no question of all: “Do you love me?”
The medieval scholars had a clear path to understanding: every aspect of knowledge came with its own distinct rules of judgment. We, when we want to take advantage of the rigor of science, have to define our problem in a form that's repeatedly testable, or abandon it. “Why is an apple sweet?”âthat's not a scientific question.
Other books
Peril on the Sea by Michael Cadnum
Tracks of the Tiger by Bear Grylls
Hot Magic by Holli Bertram
Petty Treason by Madeleine E. Robins
Stones of Aran by Tim Robinson
Montbryce Next Generation 03 - Dance of Love by Anna Markland
Green Girl by Kate Zambreno
Sleeping With The Devil by Robert Baer
Scent of Triumph by Jan Moran
Love Plays a Part by Nina Coombs Pykare
