Chances Are (3 page)
Authors: Michael Kaplan

Probability, meanwhile, gives us a method of defining a belief as it ought to exist in a reasonable mind: Truth within known limitsâand here, too, number offers a transferable standard by which we can judge that truth.
Why do we need such an abstract standard? Because our senses can fail us and our intuition is often untrustworthy. Our perception of normal and abnormal depends crucially on our field of attention: In a recent experiment, subjects who had been asked to count the number of times basketball players on one team passed the ball failed to spot a man in a gorilla suit running around the court. Even when we are trying to concentrate on an important matter of likelihoodâin a doctor's office, in a court of lawâour instincts can lead us astray, but probability can get us back on track. The economists Tversky and Kahneman devised a scenario closer to real life: a taxi sideswiping a car on a winter night. There are two taxi companies in town: Blue and Green. The latter owns 85 percent of the cabs on the road. A witness says she saw a blue taxi. Independent tests suggest she makes a correct identification 80 percent of the time. So, what color was the taxi? Almost everyone says that it was blue, because people concentrate on the reliability of the witness. But the real issue is how her reliability affects the base fact that a random taxi has an 85 percent chance of being green. When those two probabilities are combined, the chance that the taxi in question was
green
is actually 59 percentâmore likely than not. It's a conclusion we could never reach through intuitionâit requires calculation.
green
is actually 59 percentâmore likely than not. It's a conclusion we could never reach through intuitionâit requires calculation.
Â
If we want a numerical model of uncertainty, we need a way of counting the things that
can
happen and comparing that total with what actually
does
happen. “How do I love thee? Let me count the ways.” I can love you or notâthat's two possibilitiesâbut Elizabeth Barrett could love you for your wit, gravity, prudence, daring, beauty, presence, experience, or innocence. How could all these aspects, existing to a greater or lesser degree in everyone, have combined so perfectly in just oneâbrilliant Mr. Browning? How big would London have to be before she could be sure to meet him?
can
happen and comparing that total with what actually
does
happen. “How do I love thee? Let me count the ways.” I can love you or notâthat's two possibilitiesâbut Elizabeth Barrett could love you for your wit, gravity, prudence, daring, beauty, presence, experience, or innocence. How could all these aspects, existing to a greater or lesser degree in everyone, have combined so perfectly in just oneâbrilliant Mr. Browning? How big would London have to be before she could be sure to meet him?
This study of mixed characteristics is called
combinatorics
. It originated with a remarkable thirteenth-century Catalan missionary, Ramon Llull, who saw his vocation as converting the Muslims through logic.
combinatorics
. It originated with a remarkable thirteenth-century Catalan missionary, Ramon Llull, who saw his vocation as converting the Muslims through logic.
He began with nine aspects of God that all three monotheistic religions agree on: Goodness, Greatness, Eternity, Power, Wisdom, Will, Virtue, Truth, and Glory. He then grouped relations (such as Concordance, Difference, and Contrariety) and divine beings and personifications (God, Angels, Hope, Charity). He went on to show that you could assemble statements from elements of these three sets, chosen at random, and always come up with a convincing result consonant with Christian doctrine.
Substituting letters for these elements of theology, Llull wrote them on three concentric, independently movable disks: a sort of doctrinal one-armed bandit. Spinning the disks at random would produce a valid statement. Moreover, the disks made every combination of elements possible, so that no awkward proposition could be suppressed by a sneaky missionary. Ideally, Llull need simply hand over his machine to a skeptical Muslim and let him convert himself.
While God's qualities may be omnipresent, uniform, and sempiternal, the disks that define secular events have intrinsic gaps or ratchets that complicate our calculations. This is the first challenge in making a model for probability: can you devise a machine that encompasses (or, at the very least, names) all that might happen? What combination of elements makes up the event that interests you? Do these elements affect one another or do they occur independently? Finally, do all of them always contribute to the event?
These are the questions we shall be examining in this book, because they crop up whenever we consider things that don't always happen or seek what turns up only every so often. These questions underline the difference between what we think we know and what we come to knowâand even then, may not believe. Daniel Ellsberg ran an experiment in which he showed people two urns. One (he told them) contained 50 percent red and 50 percent black balls; the other, an unknown proportion of red to black balls. He offered $100 to any subject who drew a red ball from either urn. Which urn would they choose? Almost all chose the known proportion over the unknown. Then Ellsberg offered another $100 for a
black
ball; the same subjects still chose the known, 50-50 urnâeven though their first decision suggested that they thought the “unknown” urn had fewer red balls than black ones.
black
ball; the same subjects still chose the known, 50-50 urnâeven though their first decision suggested that they thought the “unknown” urn had fewer red balls than black ones.
The question remains “How right do you need to be?”âand there are large areas of life where we may not yet be right enough. A deeper worry, whether probability can really be truth, still looms like an avenging ghost. Einstein famously remarked that he did not believe God would play dice with the universe. The probabilistic reply is that perhaps the universe is playing dice with God.
2
Discovering
Even chance, which seems to hurtle on, unreined,
Submits to the bridle and government of law.
Submits to the bridle and government of law.
âBoethius
1
1
Â
Â
Â
Â
Â
Â
Â
A
nyone can talk to God; it's getting an answer that's difficult. Few of us can regularly count on divine guidance, and experience shows that going to an intermediary is not always satisfactory. The Lydian ruler Croesus planned to invade Persia, so he prudently checked with the oracle at Delphi. “If Croesus crosses the Halys, he will destroy a great empire,” said the crone in the fume-filled cavern. A true predictionâbut the empire was Croesus' own. Pressed by his enemies, Saul went to the witch of Endor and had her call up the ghost of Samuel. Samuel was hardly helpful: “The Lord hath rent the kingdom out of thine hand, and given it to thy neighbor.” The king must have left feeling like a stressed executive told by his doctor to exercise more and eat less. It's easy to see the appeal of a mechanism that would restrict Destiny to simpler, less irritating answers.
nyone can talk to God; it's getting an answer that's difficult. Few of us can regularly count on divine guidance, and experience shows that going to an intermediary is not always satisfactory. The Lydian ruler Croesus planned to invade Persia, so he prudently checked with the oracle at Delphi. “If Croesus crosses the Halys, he will destroy a great empire,” said the crone in the fume-filled cavern. A true predictionâbut the empire was Croesus' own. Pressed by his enemies, Saul went to the witch of Endor and had her call up the ghost of Samuel. Samuel was hardly helpful: “The Lord hath rent the kingdom out of thine hand, and given it to thy neighbor.” The king must have left feeling like a stressed executive told by his doctor to exercise more and eat less. It's easy to see the appeal of a mechanism that would restrict Destiny to simpler, less irritating answers.
Many things happen unpredictably, on the larger scale (defeats, disasters) and on the smaller (things dropped, things flipped). It is almost a given of human nature to posit a connection between the two scales: between local accident and universal doom. Sortilegeâtelling fortunes by casting lots or throwing diceâis a tradition that dates back almost withoutchange to before the dawn of writing. Fine cubic ivory dice (with opposite sides adding up to seven, just as in Monte Carlo or Las Vegas) accompanied pharaohs into their tombs. Even then, dice must have been a form of amusement as well as a tool of divination. What, after all, would a pharaoh need to
predict
in the afterlife? Pausanias, the Baedeker of the ancient world, nicely captures this double role of dice. He describes the great hippodromos at Elis, where, in the jumble of memorials and victory tributes, stood the Three Graces, resplendent in giltwood and ivory, holding a rose, a sprig of myrtleâand a die, “because it is the plaything of youths and maidens, who have nothing of the ugliness of old age.” Perhaps that is the secret of this shift of dice from oracle to game: the young are too busy living to be interested in fate; the old know the answer all too well.
predict
in the afterlife? Pausanias, the Baedeker of the ancient world, nicely captures this double role of dice. He describes the great hippodromos at Elis, where, in the jumble of memorials and victory tributes, stood the Three Graces, resplendent in giltwood and ivory, holding a rose, a sprig of myrtleâand a die, “because it is the plaything of youths and maidens, who have nothing of the ugliness of old age.” Perhaps that is the secret of this shift of dice from oracle to game: the young are too busy living to be interested in fate; the old know the answer all too well.
Dicing became the universal vice of the Roman aristocracy: the emperor Augustus, otherwise the pattern of self-restraint, spent whole days gambling with his cronies. Claudius wrote a book on dice and had his sedan chair rigged for playing on the move. Caligula, of course, cheated.
Meanwhile, in the dense, whispering forests across the Rhine, the Germans gave themselves completely to gamblingâwith savage literal-ness. Tacitus said: “So bold are they about winning or losing, that, when they have gambled away all else, they stake their own freedom on the final throw.”
The pure gambling games played in Roman times all seem to have been variants of
hazard
, the progenitor of modern craps, played with either dice or the knucklebones of sheep. Wherever the Roman armies camped you find hundreds of diceâa fair proportion loaded. In Augustus' favorite version of hazard the highest throw (all dice showing different faces) was called Venus, appropriately for a pastime that was also a conversation with the gods. But even with the gods, humans seek an edge: Venus was the highest throw, but also the most likely. After all, we don't go to the temple to add to our bad luck: all divination retains its popularity only as long as it gives a high proportion of favorable answers. And once you know that daisies usually have an odd number of petals, you can get anyone to love you.
hazard
, the progenitor of modern craps, played with either dice or the knucklebones of sheep. Wherever the Roman armies camped you find hundreds of diceâa fair proportion loaded. In Augustus' favorite version of hazard the highest throw (all dice showing different faces) was called Venus, appropriately for a pastime that was also a conversation with the gods. But even with the gods, humans seek an edge: Venus was the highest throw, but also the most likely. After all, we don't go to the temple to add to our bad luck: all divination retains its popularity only as long as it gives a high proportion of favorable answers. And once you know that daisies usually have an odd number of petals, you can get anyone to love you.
Condemned to live but one life and yet be aware of time beyond it, we have always looked upward for clues to the future. Astronomy was the first natural science, and the most continuously studied: the Babylonian planetary observations began four thousand years ago as a record of oracular events. Amid the ruin of ancient knowledge, the great lesson of the Babylonians was never lost: all phenomena in the solar system repeat and, by careful combinations of cyclical calculation, can be predicted. Even in the darkest days of the seventh century, the rudiments of this skill were preserved, if only to calculate the date of Easterâwhich, because of its original connection with Passover, remains an awkwardly lunar event in the solar year.
The ability to anticipate the movements of the solar system was not yet a science, though, because it said nothing about the principles that govern those movements. Medieval learning differed in essence from modern: it concerned itself with
aspects
of things, starting with the ten categories inherited from Aristotle: Substance, Quantity, Quality, Relation, Position, Place, Time, State, Action, and Affection. Medieval Nature was not a reality in itself, to be investigated until its laws became apparent; it was The Creation, with Man at its center, and its only law was God's will.
aspects
of things, starting with the ten categories inherited from Aristotle: Substance, Quantity, Quality, Relation, Position, Place, Time, State, Action, and Affection. Medieval Nature was not a reality in itself, to be investigated until its laws became apparent; it was The Creation, with Man at its center, and its only law was God's will.
Why is an apple sweet? Ask four students lounging in the sunlight in a quadrangle of the Sorbonne, seven hundred years ago, and you could receive four answers:
Â
“It is sweet because it is formed from the apple blossom, which is sweet-smelling.”
Â
“It is sweet because, being held high above the earth, it is compounded of the lighter elementsâair and fireâwith which sweetness is associated.”
Â
“It is sweet so that it may be nourishing to men and preserve them in health.”
Â
“It is sweet so that we may be reminded of the constant temptation to sin, as Adam sinned in Eden.”
The point is not whether any of these answers is correct; it is that they were
all
correct, depending on what aspect of Creation was being discussed. The test of a statement's truth was not evidence from experiment or even from observation: it was logical consistency with received texts.
all
correct, depending on what aspect of Creation was being discussed. The test of a statement's truth was not evidence from experiment or even from observation: it was logical consistency with received texts.
Dicing for money and amusement continued throughout the Middle Ages, among the high as well as the low. Even Chaucer's pious Man of Law expressed his wish that the wise might prosper using gambling terms:
O noble, prudent folk, as in this case,
Your bagges be not fill'd with ambes ace,
But with six-cinque, that runneth for your chance
At Christenmass well merry may ye dance.
Your bagges be not fill'd with ambes ace,
But with six-cinque, that runneth for your chance
At Christenmass well merry may ye dance.
Â
“Ambes ace” we'd now call snake eyes; “six-cinque” is, as you may well guess, eleven. A modern craps shooter would fit right in on the road to Canterbury.
People inevitably pay close attention to something they have money on: throughout the Middle Ages, there was a growing awareness of the innate patterns of the gameâof the number of different results you could get by rolling two or three dice. In 1283, King Alfonso the Learned of Castile, patron of astronomy, produced a set of seven treatises on dice and board games. The work is steeped in mystical numerology: seven books combine the earthly elements with the celestial trinity; the section on chess is divided into sixty-four parts; that on dice into six. Chess, for Alfonso, was a noble game, the image of the king's struggle for conquest. Dice-playing, however, was the province of tricksters; indeed, the prohibitions in Alfonso's law code revealed a surprising variety of cheating techniques.
We have come to an important moment in the history of probability: in order to cheat at a game involving repetition, you must already have a good sense of what should normally happen. Dice are the earliest and simplest form of random event generator: when you throw two dice any one of 36 combinations can occur.
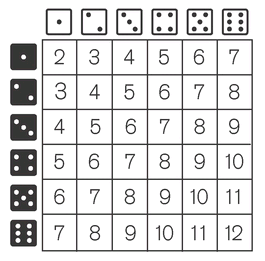
To influence the course of play in your favorâwhether you do so by shaving the dice out of true, loading them unevenly, gluing boar bristles to their edges, or simply changing their spotsâyou must first know the reality you intend to subvert. You must have all the probabilities in mind, which means you must believe (and this goes against every tenet of belief in divine providence or gambler's luck) that, were it not for your knavery,
each of those 36 possible combinations would have an equal likelihood of happening on any single throw
.
each of those 36 possible combinations would have an equal likelihood of happening on any single throw
.
Other books
Obsidian Curse by Barbra Annino
A Man Overboard by Hopkins, Shawn
The Chocolate Lovers' Diet by Carole Matthews
The Goodbye Quilt by Susan Wiggs
Wine, Tarts, & Sex by Susan Johnson
Heart Journey by Robin Owens
Glock: The Rise of America’s Gun by Paul M. Barrett
CrossFire (Love & Lies #1) by Alex Strong
Spurious by Lars Iyer
A Season of Love by Amy Clipston
