Chances Are (8 page)

Even if your taste is not for formal mathematics, you have a glimmering here of its entrancing power. This shabby man, ensconced at the window end of a greasy table in Slaughter's Tavern, had, through the clever manipulation of abstract terms, discovered—or created—a way to describe how things happen the way they “ought”: how Chance scatters itself around the central pillar of Design in the shape of a bell. “If the terms of the binomial are thought of as set upright, equally spaced and at right angles to a straight line, the extremities of the terms follow a curve.” He went on to say: “The curve so described has two inflection points, one on each side of the maximal term.” Let's look at this curve, basing our example on the numbers from row 14 of Pascal's Triangle.

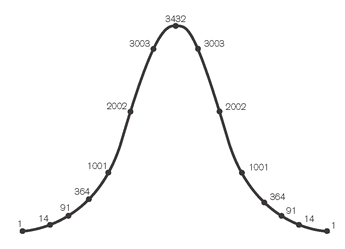
It's still pretty rough, since we have only 15 fixed points, but the form is becoming clear, particularly the “inflection points” that de Moivre mentioned: the places where the convex curve down from the center changes into a concave curve out toward the sides. Those are the most interesting points on the curve; de Moivre calculated their distance from the midpoint of the curve as 1/2√
n
, for n trials. This number is what statisticians now call the
standard deviation
, one of their most important terms—and its importance stems from what de Moivre did next.

Since the newly invented calculus gave him the ability to measure the area under the curve, de Moivre decided to see what fraction of that area was taken up by the vertical slice of area between the midpoint and the inflection point. Again, the calculation involved an infinite series that converged to a single, disconcertingly precise figure: 0.341344 (assuming that the total area under the curve equals 1). So the area covered by the curve between its two inflection points is double that: 0.682688.

Once again, the power of formal mathematics has handed us a golden key—but to what? To the orderly expectation of random behavior. It reveals that, for an experiment with equal chances of success or failure, we can expect a bit more than two thirds of our results to be within 1/2
√n
of our expected middle value. The more trials we make, the bigger
n
becomes and the closer the total results come to their inherent probability. So, as de Moivre showed, if we toss a coin 3,600 times, the probability is 0.682688 that we will get between 1,770 and 1,830 heads, and the probability is 0.99874—as close to certainty as most mortals know—that we will toss between 1,710 and 1,890 heads. Make yet more trials, and the window will tighten as the curve becomes ever taller and narrower: the behavior of the experiment is inherent in the nature of the curve.

De Moivre saw that his curve was not only the expression of the laws of probability, but the sign by which previously incoherent data revealed their subjugation to those laws.

 

De Moivre saw God revealed in the pattern of randomness. Having been banished from the deterministic physical world by Descartes, Divinity returns in the unexpected mathematical perfection of chance events. The bell curve shows the trace of an almighty hand—though, of course, particular cases can lie well off the midpoint. De Moivre himself was just such an outlier. He gained little from his genius; even his curves are now named for Gauss and Poisson. He was always a bit too much or too little for the world he lived in, but his own series at last converged at the age of eighty-seven. According to the story, having noticed that he was sleeping a little longer every day, he predicted the day when he would never awake . . . and on that day he died, as the bill of death put it, of “a somnolence.”

 

The essence of calculus is its ability to conjure precision out of imprecision. No genie could ever sum all the terms of your infinite series, no guardian angel tell you the exact slope of your curve at a single point—but calculus can give you an answer within any desired degree of exactitude. Nothing
real
in the eighteenth century, not even astronomy, actually demanded a measurement correct to four decimal places, yet de Moivre could provide answers far more accurate than that, simply by working out approximations with a thick carpenter's pencil on the back of a discarded ballad-sheet.

The power this technique offered to science obscured, at least for a time, the philosophical problems it brought with it, the deepest of which may have been troubling you since we finished with Pascal's Triangle. Its beautifully symmetrical rows give us a perfect, Platonic representation of the fall of heads and tails, but we have not been talking about anything that actually happens in this world. Our constructs, beautiful as they may be, are descriptions of the behavior of chance in the abstract, as true (or, rather, as valid) at any point in space or time as here and now. To achieve this validity, they depend on the unique ability of mathematics to map the unobtainable and inaccessible: sums of series that go on forever, distances that collapse to zero.

Thus, we get our results by pointing—albeit precisely—at places we can never reach. What has more recently been called “the unreasonable effectiveness of mathematics in the natural sciences” is bought at the price of making a mental leap into the abstract at the point of recording an observation: we assign it to a model universe, at once simpler and purer than the one we inhabit. Dice, after all, are
not
inherently random: they are a very complicated but determined physical system. Coins need not be ruled by chance; a competent amateur magician learns to flip only heads, pinning us forever to one side of the normal distribution. So when we take up the tools of probability and use them on experience, what are they actually telling us? Something about the real world and its hidden structure? Something about the nature of observation? Or something about our own judgment? These questions are not rhetorical; and if they worry you, you are in the best of company.

 

Such worries, however, were far from anyone's mind at the height of the Enlightenment, when the mutually supporting advances of mathematics and the natural sciences convinced most cultured observers that calculus was not just the grammar but the content of Reason. Mathematics was the natural model for the self-evident truths which were such a distinguishing feature of Enlightenment belief, from Newtonian physics to revolutionary politics.

 

The speaker was Pierre Simon, Marquis de Laplace, at once the most brilliant and the most fortunate scientist of his generation. Son of a Norman smallholder, from his arrival in Paris in 1767 at the age of eighteen until his death in 1827—through all the years of discord, revolution, slaughter, empire, war, restoration, and again discord—Laplace never knew misfortune or danger. Ennobled by Napoleon, promoted to marquis by Louis XVIII, he proceeded from honor to honor in an imperturbable orbit.

Laplace's abilities straddled the crystalline purity of first principles and the messy particularity of actual phenomena. Beyond his virtual invention of the calculus of probability, he made significant mathematical contributions to the sciences of gravitation, thermodynamics, electricity, and magnetism. His accomplishments in physical astronomy were legendary; in effect, the science had to wait for new data before it could have anything further to say.

The fullest expression of Laplace's contribution to the theory of probability is his
Théorie analytique
of 1812. Although he said that probability was simply common sense expressed in mathematical language, his theory required the creation of an entirely new branch of calculus, and is presented so densely that it still daunts professional mathematicians. His assistant remembered the great man himself wrestling for an hour to retrace the mental steps he had dismissed with just one “
il est aisé à voir.”
Easy to see, he meant, in retrospect—blossoming from first principles by agreed forms of reasoning.

Laplace's universe is entirely determined. He famously claimed that if it were possible for a single intelligence just to know the current position and velocity of all particles, every future event would be predictable—it is only we, with our puny senses, our inefficient instruments and our hasty judgments, who fail to anticipate its revolutions.

Probability therefore is a kind of corrective lens, allowing us, through an understanding of the nature of Chance, to refine our conclusions and approximate, if not achieve, the perfection of Design. The significance of de Moivre's bell curve is that it describes how what we observe scatters around the pole of immutable law—the “generating function” that represents the ideal behavior of a system. The curve is a tool that cancels out the inescapable error in our data and reveals the one, pure, truth—the secrets not just of the stars but of all physical processes.

Showing the same confidence with which the French Revolution devised the metric system and the decimal calendar, Laplace thought it only logical to extend his principles from the science to morals and politics. Voting, forming assemblies, evaluating legal testimony—all, he felt, would proceed more reasonably if first modeled as the dice-rollings, coin-tossings, lotteries, and urns full of pebbles in probability problems. Probability would damp the terrible fluctuations that can blight the lives of generations, and lead us to the broad sunlit uplands of the Empire of Reason.

Sadly, the fundamental unit of the metric system is not a perfect fraction of the Earth's circumference, and the French Revolutionary calendar is now remembered only in lobster Thermidor. As for Laplace's injunction to “examine critically our own opinions and weigh with impartiality their respective probabilities”—how, exactly, should we do this? Well . . .
il est aisé à voir
.

Nevertheless, by redefining probability from an inherent property of random events to a proportion derived from observations, Laplace helped shape the future of science by prescribing which phenomena it would choose to observe: those that could be entered neatly into probability calculations. And because he put the mind of the observer, rather than the nature of creation, at the center of science, he broke forever Pascal's hope that faith and scientific inquiry could sit comfortably together.

Not a religious man, Laplace seemed almost to resent the implication that a mere divinity could disturb the perfect regularity of celestial affairs. When Napoleon teasingly remarked that he had seen no mention of the creator of the universe in the
Méchanique céleste,
Laplace bridled: “Sire, I had no need of that hypothesis.” He seemed genuinely pained that as great a mind as Pascal's should give credence to miracles. And so, since probability is a matter of what we can see in this world rather than what could happen anywhere, Laplace made quick use of it to bring Pascal's Wager fluttering down to earth.

Here is his reasoning—and as always, the crux of the argument is in its initial setting out. Assuming that our choice is between belief in God or not, how did we know we
had
this choice? Because we had been
told
about it: witnesses, from evangelists to parish priests, affirmed to us God's promise that belief leads to an infinity of happy lives. That—not the promise itself—is the observation. Laplace chooses a lottery as his model, which fits well enough with Pascal's idea that even if the odds against the existence of God approach the infinite, the size of the prize compared with our entry stake makes the game worth playing. Let's say that Pascal's lottery is represented by a series of numbered balls, each of which returns that number of happy lives for our stake of one life. We ourselves don't see the draw, but a witness tells us that we have won the top prize. How credible is that testimony?

Obviously, it's very much in the interest of these particular witnesses to affirm that we have won, but let us simply assume that the likelihood of their being able to speak with absolute accuracy on such an important matter is, say, one-half. Let us assume moreover the fewest number of happy lives that Pascal claimed would make his wager a guaranteed win: three. There are three balls in the urn; the draw is made. The witness says: “Congratulations! It's number 3!” Now he is either telling the truth or not. If he is telling the truth, we calculate the probability of observing this by multiplying the innate probability of drawing number 3 (1/3) by the probability that the witness is telling the truth (1/2), and we come up with 1/6.