Nonplussed!
Authors: Julian Havil


MATHEMATICAL PROOF OF IMPLAUSIBLE IDEAS
Julian Havil
PRINCETON UNIVERSITY PRESS
PRINCETON AND OXFORD
Copyright © 2007 by Julian Havil
Published by Princeton University Press,
41 William Street, Princeton, New Jersey 08540
In the United Kingdom: Princeton University Press,
6 Oxford Street, Woodstock, Oxfordshire OX20 1TW
press.princeton.edu
All Rights Reserved
Fourth printing, and first paperback printing, 2010
Paperback ISBN: 978-0-691-14822-9
The Library of Congress has catalogued the cloth edition of this book as follows
Havil, Julian, 1952-
Nonplussed! : mathematical proof of implausible ideas / Julian Havil.
p. cm.
Includes index.
ISBN-13: 978-0-691-12056-0 (acid-free paper)
ISBN-10: 0-691-12056-0 (acid-free paper)
1. Mathematics Miscellanea. 2. Mathematical recreations.
3. Paradox Mathematics. I. Title.
QA99.H38 2006
510 dc22 2006009994
British Library Cataloguing-in-Publication Data is available
This book has been composed in Lucida
Typeset by T&T Productions Ltd, London
Printed on acid-free paper ∞
Printed in the United States of America
5 7 9 10 8 6 4
To Anne
for whom my love is monotone increasing
and unbounded above
Time flies like an arrow. Fruit flies like a banana.
Groucho Marx
Do I contradict myself? Very well then I contradict myself. I am large, I contain multitudes.
Walt Whitman
Mathematics is not a careful march down a well-cleared highway, but a journey into a strange wilderness, where the explorers often get lost. Rigour should be a signal to the historian that the maps have been made, and the real explorers have gone elsewhere.
W. S. Anglin
C
HAPTER
1
Three Tennis Paradoxes
C
HAPTER
6
Conway’s Chequerboard Army
A
PPENDIX
A
The Inclusion–Exclusion Principle
A
PPENDIX
B
The Binomial Inversion Formula
Epistle to the Reader
I HAVE put into thy hands what has been the diversion of some of my idle and heavy hours. If it has the good luck to prove so of any of thine, and thou hast but half so much pleasure in reading as I had in writing it, thou wilt as little think thy money, as I do my pains, ill bestowed. Mistake not this for a commendation of my work; nor conclude, because I was pleased with the doing of it, that therefore I am fondly taken with it now it is done. He that hawks at larks and sparrows has no less sport, though a much less considerable quarry, than he that flies at nobler game: and he is little acquainted with the subject of this treatise – the UNDERSTANDING –who does not know that, as it is the most elevated faculty of the soul, so it is employed with a greater and more constant delight than any of the other. Its searches after truth are a sort of hawking and hunting, wherein the very pursuit makes a great part of the pleasure. Every step the mind takes in its progress towards Knowledge makes some discovery, which is not only new, but the best too, for the time at least.
These words, recorded as being written in Dorset Court, London, on 24 May 1689, are those of the British philosopher and polymath John Locke and form the first part of his Preface (or Epistle to the Reader) of his monumental work of 1690,
An Essay Concerning Human Understanding
.
It is our preface too.
I should like to thank my headmaster, Dr Ralph Townsend, for his support, particularly through sabbatical leave, former student Tom Pocock for his enthusiasm and honest opinions, the reviewers for their helpful views, Design Science for creating Mathtype™ and Wolfram Research for creating Mathematica™. Further, my grateful thanks are due to Jonathan Wainwright of T&T Productions Ltd for his meticulous and patient work and to my editor, Vickie Kearn, for her own patient understanding and enthusiasm. Finally, I join a long list of those who have thanked Martin Gardner for being a lifelong inspiration.

Alice laughed: ‘There’s no use trying,’ she said; ‘one can’t believe impossible things.’
‘I daresay you haven’t had much practice,’ said the Queen. ‘When I was younger, I always did it for half an hour a day. Why, sometimes I’ve believed as many as six impossible things before breakfast.’
‘Where shall I begin,’ she asked.
‘Begin at the beginning,’ the king said, ‘and stop when you get to an end.’
Lewis Carroll
It does not take a student of mathematics long to discover results which are surprising or clever or both and for which the explanations themselves might enjoy those same virtues. In the author’s case it is probable that in the long past the ‘coin rolling around a coin’ puzzle provided Carroll’s beginning and a welcome, if temporary, release from the dry challenges of elementary algebra:
Two identical coins of equal radius are placed side by side, with one of them fixed. Starting head up and without slipping, rotate one about the other until it is on the other side of the fixed coin, as shown in
figure 1
.
Is the rotated coin now head up or head down?
Within a random group of people both answers are likely to be proffered as being ‘obviously true’, yet one of them is false and a quiet experiment with two coins quickly reveals which. We must prove the fact though, and too much knowledge is dangerous here: fix on a point on the circumference of the moving circle and we have an epicycloid to consider (or, more precisely, a cardioid) – and there could be hard mathematics to deal with.
Alternatively, concentrate on the path of the centre of the moving coin and let us suppose that the common radii of the coins are
r
. During the motion, the path traced out by this centre is a semicircle, whose centre is itself the centre of the fixed coin and whose radius is 2
r
; the motion will cause the centre to move a distance
π
(2
r) =
2
πr
.
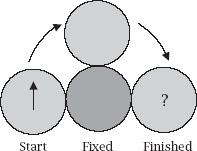
Figure 1.
A coin rolling around another fixed coin.
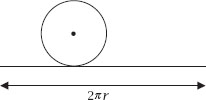
Figure 2.
The situation simplified.
Now simplify matters and consider the moving coin rotating without slipping along a straight line of length 2
πr
, the distance moved by its centre, as shown in
figure 2
. It is perfectly clear that it will have turned through 360
0
– and so be the right way up.
When it is first seen, the result is indeed surprising – and the solution clever.
It is a suitable preliminary example as this book chronicles a miscellany of the surprising, with a nod towards the clever, at least in the judgement of its author. The choice of what to include or, more painfully, what to exclude has been justly difficult to make and a balance has been found which recognizes the diversity of the surprising as well as the large role played by probability and statistics in bringing about surprise: it is they
and the infinite which abound in the counterintuitive; other areas of mathematics dally with it. To reflect all of this, the fourteen chapters which constitute the book are divided evenly and alternate between results which intrinsically depend on probability and statistics and those which arise in other, widely diverse, areas; one such is the infinite. To reflect these tensions further, this is the first of two such books, the second providing the opportunity to embrace what the reader may have considered as unfortunate omissions. Wherever it has been possible, the provenance of the result in question has been discussed, with a considerable emphasis placed on historical context; no mathematics grows like Topsy, someone at some time has developed it.
Apart from
chapter 13
(and where else could that material be placed?), the level of mathematics increases as the book progresses, but none of it is beyond a committed senior high school student: looking hard is not at all the same as being hard. It is hoped that the reader, young or not-so-young, will find something in the pages that follow to inform or remind him or her of the frailty of the intuition we routinely employ to guide us through our everyday lives, but which is so easily confounded – only to be replaced by the uncompromising reason of mathematical argument.

THREE TENNIS PARADOXES
So that as tennis is a game of no use in itself, but of great use in respect it maketh a quick eye and a body ready to put itself into all postures; so in the mathematics, that use which is collateral and intervenient is no less worthy than that which is principal and intended.
Roger Bacon
In this first chapter we will look at three examples of sport-related counterintuitive phenomena: the first two couched in terms of tennis, the third intrinsically connected with it.
Winning a Tournament
The late Leo Moser posed this first problem during his long association with the University of Alberta. Suppose that there are three members of a club who decide to embark on a private tournament: a new member M, his friend F (who is a better player) and the club’s top player T.
M is encouraged by F and by the offer of a prize if M wins at least two games in a row, played alternately against himself and T.
It would seem sensible for M to choose to play more against his friend F than the top player T, but if we look at the probabilities
associated with the two alternative sequences of play, FTF and TFT, matters take on a very different look. Suppose that we write
f
as the probability of M beating F and
t
as the probability of M beating T (and assume independence).
Table 1.1.
The situation if the new member plays his friend twice.

Table 1.2.
The situation if the new member plays the club’s top player twice.
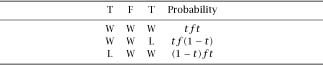
If M does choose to play F twice, we have
table 1.1
, which lists the chances of winning the prize.
This gives a total probability of winning the prize of
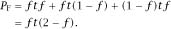
Now suppose that M chooses the seemingly worse alternative of playing T twice, then
table 1.2
gives the corresponding probabilities, and the total probability of winning the prize becomes
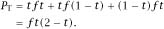
Since the top player is a better player than the friend,
t < f
and so 2 -
t
2 -
f
, which makes
ft
(2 -
t
) >
ft
(2 -
f
) and
P
T
>
P
F
. Therefore, playing the top player twice is, in fact, the better option.
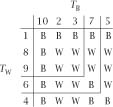
Table 1.3.
Outcome of an all-plays-all tournament between the various teams.
Logical calm is restored if we look at the expected number of wins. With FTF it is
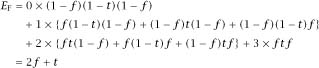
and a similar calculation for TFT yields
E
T
= 2
t + f
.
Since
f > t
, 2
f - f
2
t - t
and so 2
f + t >
2
t + f
, which means that
E
F
>
E
T
– and that we
would
expect!
Forming a Team
Now let us address a hidden pitfall in team selection.
A selection of 10 tennis players is made, ranked 1 (the worst player, W) to 10 (the best player, B). Suppose now that W challenges B to a competition of all-plays-all in which he can chose the two best remaining players and B, to make it fair, must choose the two worst remaining players.
The challenge accepted, W’s team is
T
W
= {1, 8, 9} and B’s team is
T
B
= {10, 2, 3}.
Table 1.3
shows the (presumed) inevitable out-come of the tournament; at this stage we are interested only in the upper left corner. We can see that W’s disadvantage has not been overcome since
T
B
beats
T
W
5 games to 4.
Table 1.4.
The average rankings of each of the three pairs of teams.

The remaining players are
{
4,5,6,7} and W reissues the challenge, telling B that he can add to his team one of the remaining players and then he would do the same from the remainder; of course, both B and W choose the best remaining players, who are ranked 7 and 6 respectively. The teams are now
T
W
= {1, 8, 9, 6} and
T
B
= {
10, 2, 3, 7
}
and the extended
table 1.3
now shows that, in spite of B adding the better player to his team, the result is worse for him, with an 8–8 tie.
Finally, the challenge is reissued under the same conditions and the teams finally become
T
W
= {1,8,9,6,4} and
T
B
= {
10,2,3,7,5} and this time the full
table 1.3
shows that
T
W
now beats
T
B
13–12.
A losing team has become a winning team by adding in worse players than the opposition.
Table 1.4
shows, in each of the three cases, the average ranking of the two teams. We can see that in each case the
T
B
team has an average ranking less than that of the
T
W
team and that the average ranking is increasing for
T
B
and decreasing (or staying steady) for
T
W
as new members join. This has resonances with the simple (but significant) paradox known as the
Will Rogers Phenomenon
.
Interstate migration brought about by the American Great Depression of the 1930s caused Will Rogers, the wisecracking, lariat-throwing people’s philosopher, to remark that
When the Okies left Oklahoma and moved to California, they raised the intellectual level in both states.
Rogers, an ‘Okie’ (native of Oklahoma), was making a quip, of course, but if we take the theoretical case that the migration was from the ranks of the least intelligent of Oklahoma, all of whom were more intelligent than the native Californians(!), then what he quipped would obviously be true. The result is more subtle,
though. For example, if we consider the two sets
A = {
1,2,3,4} and
B = {
5,6,7,8,9}, supposedly ranked by intelligence level (1 low, 9 high), the average ranking of
A
is 2
.
5 and that of
B
is 7. However, if we move the 5 ranking from
B
to
A
we have that
A = {
1,2,3,4,5} and
B = {
6,7,8,9} and the average ranking of
A
is now 3 and that of
B
is 7
.
5: both average intelligence levels have risen.
